Introduction
There has always been a strong debate about alternative macroeconomic schools of thought (see e.g. Greenwald et al. 1988; Greenwald & Stiglitz 1993) 1, but, at the dawn of 2008, a new consensus emerged: the New Neoclassical Synthesis (NNS) (see e.g. Goodfriend 2007; Woodford 2009), grounded upon Dynamic Stochastic General Equilibrium (DSGE) models2. A large number of NNS contributions claimed indeed that monetary – and, more generally, economic – policy was finally becoming more of a science (Mishkin 2007; Galí & Gertler 2007; Goodfriend 2007; Taylor 2007), and macroeconomic policies could finally resort on the application of a core set of "scientific principles" (Mishkin 2007, p.1).
Furthermore, the available toolbox of economic policy rules was deemed to work exceptionally well not only for normative purposes, but also for descriptive ones. For example, Taylor (2007) argued that "while monetary policy rules cannot, of course, explain all of economics, they can explain a great deal" (p.1) and also that "although the theory was originally designed for normative reasons, it has turned out to have positive implications which validate it scientifically" (abstract). Given these Panglossian premises, scientific discussions on economic policy seemed therefore to be ultimately confined to either fine-tuning the "consensus" model, or assessing the extent to which elements of art (appropriable by the policy maker) still existed in the conduct of policies (Mishkin 2007)3.
The DSGE model hegemony was not just confined to the academia — "an aphorism among macroeconomists today is that if you have a coherent story to propose, you can do it in a suitably elaborate DSGE model" (Chari et al. 2009) — but it reached policy makers and central banks (without surprise the finance industry was the only exception, Smith 2014). Unfortunately, as it happened with two famous statements made, respectively, by Francis Fukuyama (1992) about an alleged "end of history", and by many physicists in the recent debate on a purported "end of physics" (see, e.g., Lindley 1994), these positions have been proven to be substantially wrong by subsequent events. Indeed, the "perfect storm" that followed the bankruptcy of Lehman Brothers on September 15, 2008 brought financial markets on the edge of collapse causing in turn the worst recession developed economies have ever seen since the Great Depression, and is still threatening the stability of many world countries.
What is worse, mainstream DSGE-based macroeconomics appears to be badly equipped to deal with the big turmoil we have been facing. As Krugman (2011) points out, not only orthodox macroeconomists did not forecast the crisis, but they did not even admit the possibility of such event and, even worse, they did not provide any useful advice to policy makers to put back the economy on a steady growth path (see also Stiglitz 2011, 2015). On the same line, DeLong (2011) reports that when the former U.S. secretary Lawrence Summers was asked what economics can offer to understand the crisis, he quoted the works of Bagehot, Minsky and Kindleberger, appeared more than 30 years ago. This is so because the DSGE approach "has become so mesmerized with its own internal logic that it has begun to confuse the precision it has achieved about its own world with the precision that it has about the real one" (Caballero 2010, p. 85).
In that respect, the Great Recessions turned out to be a "natural experiment" for economic analysis, showing the inadequacy of the predominant theoretical frameworks. DSGE scholars have reacted to such a failure trying to amend their models with e.g. financial frictions, homeopathic doses of agent heterogeneity and exogenous fat-tailed shocks (see e.g. Lindé et al. 2016). At the same time, an increasing number of leading economists have claimed that the 2008 "economic crisis is a crisis for economic theory" (Kirman 2010, 2016; Colander et al. 2009; Krugman 2009; Farmer & Foley 2009; Krugman 2011; Caballero 2010; Stiglitz 2011, 2015; Kay 2011; Dosi 2012; De-Long 2011; Romer 2016). Their view, which we fully share here, is that the basic assumptions of mainstream DSGE models, e.g. rational expectations, representative agents, perfect markets etc., prevent the understanding of basic phenomena underlying the current economic crisis and, more generally, macroeconomic dynamics4.
In order to better articulate these points, we extend and update here the discussion presented in Fagiolo & Roventini (2012). We argue that new developments and extensions of DSGE models are certainly welcome, but instead of performing such a Ptolemaic exercise (Stiglitz 2011, 2015; Dosi 2012; Caballero 2010) —adding a plethora of new "epicycles" to fix flawed models— economists should consider the economy as a complex evolving system, i.e. as an ecology populated by heterogeneous agents whose far-from-equilibrium interactions continuously change the structure of the system (more on that in Farmer & Foley 2009; Kirman 2010, 2016; Dosi 2012; Rosser 2011; Battiston et al. 2016). This is indeed the methodological core of agent-based computational economics (ACE) (e.g. Tesfatsion 2006a; LeBaron & Tesfatsion 2008), a stream of research whose keywords are heterogeneity, bounded rationality, endogenous out-of-equilibrium dynamics, and direct interactions among economic agents. In this article, we discuss how this approach allows to build models that, from a descriptive perspective, are able to reproduce many features of the 2008 economic crisis, such as, e.g., asset bubbles, resilience of interbank networks, self-organized criticality, financial accelerator dynamics (see Section 5 for more details).
Furthermore, on the normative side, due to the extreme flexibility of the set of assumptions regarding agent behaviors and interactions, ACE models (often called agent-based models, ABMs) represent an exceptional laboratory to design policies and to test their effects on macroeconomic dynamics. Indeed, as Section 6 shows, an increasing number of macroeconomic policy applications have been already devised and explored concerning fiscal and monetary policies, bank regulation, structural reforms in the labor market, and climate change policies.
Certainly, given its relatively young age, also in the ACE approach there are still open issues that should be addressed. The most important ones concern empirical validation, over-parametrization, estimation and calibration, and comparability between different models. Nevertheless, papers addressing such issues have blossomed in recent years (cf. Section 5). Furthermore, the success of ACE models in delivering policy implications, while simultaneously explaining the observed micro and macro stylized facts, are encouraging for the development of a new way of doing macroeconomic theory.
The structure of this paper essentially mimics its predecessor (Fagiolo & Roventini 2012), whilst extending and updating all sections with new material coming from recent methodological improvements and new applications in both the DSGE and ABM camps. In particular, Section 2 surveys the approach to policy of the New Neoclassical Synthesis. In Section 3, we discuss the main theoretical and empirical difficulties of DSGE models. Section 4 reviews the recent developments in DSGE macroeconomics. In Section 5, we instead introduce the ACE paradigm and in Section 6 we review some policy macroeconomic applications in this field. Section 7 concludes by telegraphically accounting for some methodological issues related to policy in ACE models and the ensuing research avenues that these problems open up.
DSGE Models and Economic Policy
Let us begin by presenting how policy analysis is usually carried out in DSGE models, which are at the center of the New Neoclassical Synthesis (Goodfriend & King 1997). The canonical DSGE model has a real-business-cycle (RBC) core supplemented with monopolistic competition, nominal imperfections and a monetary policy rule (for a more detailed exposition of the DSGE model, cf. Clarida et al. 1999; Woodford 2003; Galí & Gertler 2007).
In line with the RBC tradition, the backbone of DSGE models is the standard stochastic neoclassical growth model with variable labor supply: the economy is populated by an infinitely-lived representative household, and by a representative firm, whose homogenous production technology is hit by exogenous shocks. All agents form their expectations rationally (Muth 1961). The New Keynesian flavor of the model is provided by money, monopolistic competition and sticky prices. Money has usually only the function of unit of account and the nominal rigidities incarnated in sticky prices allow monetary policy to affect real variables in the short run. The RBC scaffold of the model allows the computation of the "natural" level of output and real interest rate, which is the equilibrium values of the two variables under perfectly flexible prices. In line with the Wickselian tradition, the "natural" output and interest rate constitute a benchmark for monetary policy: the central bank cannot persistently push the output and the interest rate away from their "natural" values without creating inflation or deflation. Finally, imperfect competition and possibly other real rigidity imply that the "natural" level of output is not socially efficient.
The plain vanilla version of the DSGE model is represented by three equations: the expectation-augmented IS equation, the New Keynesian Phillips (NKP) curve, and a monetary policy rule. The expectation-augmented IS equation constitutes the aggregate-demand building block of the NNS model and it stems from the goods market-clearing condition and the Euler equation of the representative household (under the assumption of perfect capital markets):
| $$\tilde{y_{t}}=E_{t}\tilde{y}_{t+1}-\sigma(i_{t}-E_{t}\pi_{t+1}-r_{t}^{n}), $$ | (1) |
The aggregate-supply building block of the NNS model boils down to a New Keynesian Phillips curve. By combining the Dixit & Stiglitz (1977) model of monopolistic competition and the Calvo (1983) model of staggered prices, one obtains that in any given period firms allowed to adjust prices fix them as a weighted average of the current and expected future nominal marginal cost. The NKP curve can be obtained by combining the log-linear approximation of the optimal price-setting choice, the price index and the labor-market equilibrium:
| $$ \pi_{t}=\kappa \tilde{y}_{t} + \beta E_{t}\pi_{t+1}+u_{t}, $$ | (2) |
The model is closed with the monetary policy rule. The derivation of the optimal monetary policy rule is carried out adopting a welfare criterion: taking a second-order Taylor series approximation of the utility of the representative household, one can derive a welfare loss function for the central bank that is quadratic in inflation and in deviations of output from its socially efficient level (see Woodford 2010). Alternatively, one can plug a "simple" rule such as the Taylor (1993) rule (see Howitt 1992 and Taylor & Williams 2010, for a survey; more detail below)
| $$ i^{\tau}_{t}=r_{t}^{n} + \phi_{\pi} \pi_{t} + \phi_{y}\tilde{y}_{t}, $$ | (3) |
Before performing policy exercises with DSGE models, one ought to assess their empirical performance and calibrate their parameters. At this stage, in medium-scale DSGE model (see e.g. Christiano et al. 2005; Smets & Wouters 2003, 2007) different type of shocks (e.g. government spending and private consumption disturbances) are usually added to improve the estimation. Moreover, as the assumption of forward-looking agents prevents DSGE models to match the econometric evidence on the co-movements of nominal and real variables (e.g., the response of output and inflation as to a monetary policy shock is too fast to match the gradual adjustment showed by the corresponding empirical impulse-response functions), a legion of "frictions" – often not justified on the theoretical ground – such as predetermined price and spending decisions, indexation of prices and wages to past inflation, sticky wages, habit formation in preferences for consumption, adjustment costs in investment, variable capital utilization, etc. However, in almost all DSGE models the labor market is not explicitly modeled and unemployment is not contemplated (a notable exception is Blanchard & Galí 2010, who introduce a search and matching model of labor market).
From an econometric perspective, DSGE models are naturally represented as a vector auto-regression (VAR) model. The estimation of the resulting econometric model is usually carried out either with a limited information approach or by full-information likelihood-based methods (see Fernandez-Villaverde et al. 2016, for a detailed description of solution and estimation methods for DSGE models).
Limited information approach. The strategy of the limited information approach to estimate and evaluate DSGE models is usually the following (e.g., Rotemberg & Woodford 1999; Christiano et al. 2005):
- Specify the monetary policy rule and the laws of motion for the shocks.
- Split the parameters in two sets and calibrate the parameters in the first set providing some theoretical or empirical justifications for the chosen values.
- After having fixed the timing of the endogenous variables, estimate via OLS the coefficients of the monetary policy rule and obtain the impulse-response functions as to a monetary policy shock.
- Recover the second set of parameters by minimizing the distance between the model-generated and empirical impulse-response functions.
- Finally, given the structural parameter values and the VAR, identify the other structural shocks by imposing, if necessary, additional restrictions.
The empirical performance of the model is then measured by comparing the impulse-response functions generated by the model with the empirical ones.
Full information approach. The full information approach was initially discarded to estimate DSGE models because maximum likelihood methods deliver implausible estimates. However, with the introduction of Bayesian techniques, the full information approach regained popularity and it is now commonly employed (see e.g. Smets & Wouters 2003, 2007). Bayesian estimation is carried out according to the following steps:
- Place if necessary some restrictions on the shocks in order to allow later identification. For instance Smets & Wouters (2003) assume that technology and preference shocks follow an independent first-order autoregressive process with i.i.d. Gaussian error terms, whereas "cost-push" and monetary policy shocks are i.i.d. Normal white noise processes.
- Employ the Kalman filter to compute the likelihood function of the observed time series.
- Form the prior distribution of the parameters by choosing their initial values through calibration, preliminary exploratory exercises, and/or to get some desired statistical properties.
- Combine the likelihood function with the prior distribution of the parameters to obtain the posterior density, which is then used to compute parameter estimates.
One can then assess the empirical performance of the estimated DSGE model comparing its marginal likelihood with the one of standard VAR models (i.e. the Bayes factor) and the model-generated cross-covariances vis-á-vis the empirical ones.
Policy analysis. Once one has recovered the parameters of the model by estimation or calibration and has identified the structural shocks, policy-analysis exercises can finally be carried out. More specifically, after having derived the welfare loss function, one can assess the performance of the subset of "simple" policy rules that guarantee the existence of a determinate equilibrium or the more appropriate parametrization within the class of optimal monetary policy rules. This can be done via simulation, by buffeting the DSGE model with different structural shocks and computing the resulting variance of inflation and the output gap and the associated welfare losses of the different monetary policy rules and parameterizations employed (see e.g. Rotemberg & Woodford 1999; Galí & Gertler 2007). In practice, assuming that the DSGE model is the "true" data generating process of the available time series, one is evaluating how the economy portrayed by the model would react to the same structural shocks observed in the past if the monetary policy followed by the central bank were different. Adding the public sector to the plain-vanilla DSGE model, one can also study the effects of fiscal policies. More specifically, one can compute the impulse response functions to analyze the impact on GDP dynamics of government spending and tax shocks (see e.g. Cogan et al. 2009).
Policy with DSGE Models: A Safe Exercise?
There are three types of problems which undermine the usefulness of DSGE models for policy analyses. Such problems are theoretical, empirical and related to the political economy of DSGE models. Let us discuss each of them in turn.
Theoretical issues
As DSGE models are general equilibrium models (GE) rooted in the Arrow-Debreu tradition with some minor non-Walrasian features (e.g., sticky prices), they are plagued by the same well-known problems of GE models (see Kirman 1989, for a classical reference).
First, the well-known Sonnenschein (1972), Mantel (1974), Debreu (1974) theorems prove that the uniqueness and stability of the general equilibrium cannot be attained even if one places stringent and unrealistic assumptions about agents. Moreover, Saari & Simon (1978) show that an infinite amount of information is required to reach the equilibrium for any initial price vector.
Given such nihilist conclusions, neoclassical economists took the short-cut of the representative agent (RA) to obtain stable and unique equilibrium. Indeed, if the choices of heterogeneous agents collapse to the RA ones, one can circumvent all the aggregation problems and develop GE macroeconomic models with rigorous Walrasian micro-foundations grounded on rationality and constrained optimization.
However, the RA assumption is far from being innocent: there are (at least) four reasons for which it cannot be defended (Kirman 1992)6. First, individual rationality does not imply aggregate rationality: one cannot provide any formal justification to support the assumption that at the macro level agents behave as a maximizing individual. Second, even if one forgets the previous point, one cannot safely perform policy analyses with RA macro models, because the reactions of the representative agent to shocks or parameter changes may not coincide with the aggregate reactions of the represented agents. Third, even if the first two problems are solved, there may be cases where given two situations a and b, the representative agent prefers a, whereas all the represented individuals prefer b. Finally, the RA assumption introduces additional difficulties at the empirical level, because whenever one tests a proposition delivered by a RA model, one is also jointly testing the very RA hypothesis. Hence, the rejection of the latter hypothesis may show up in the rejection of the model proposition that is being tested. Forni & Lippi (1997, 1999) show that basic properties of linear dynamic micro-economic models are not preserved by aggregation if agents are heterogeneous (see also Pesaran & Chudik 2011). For instance, micro-economic co-integration does not lead to macroeconomic co-integration, Granger-causality may not appear at the micro level, but it may emerge at the macro level, aggregation of static micro-equations may produce dynamic macro-equations. As a consequence, one can safely test the macroeconomic implications of micro-economic theories only if agents’ heterogeneity is explicitly and carefully modeled.
More generally, the representative agent assumption implies that there is a one-to-one correspondence between the micro and macro levels. In particular, macroeconomic dynamics is compressed into microeconomics. Below we will see that this simplification prevents DSGE models to account for complex phenomena.
The last theoretical issue concerns the existence and determinacy of the system of rational-expectation equilibrium conditions of DSGE models. If the exogenous shocks and the fluctuations generated by the monetary policy rule are "small", and the "Taylor principle" holds (i.e., \(\phi_{\pi}>1\), see eq. 3), the rational-expectation equilibrium of the DSGE model presented in Section 2 (Woodford 2003)7 exists and is locally determinate. This result allows one to compute impulse-response functions in presence of "small" shocks or parameter changes and to safely employ log-linear approximations around the steady state. Unfortunately, the existence of a local determinate equilibrium does not rule out the possibility of multiple equilibria at the global level (see e.g. Schmitt-Grohé & Uribe 2000; Benhabib et al. 2001; Ascari & Ropele 2009). This is a serious issue because there is always the possibility, e.g. if the laws of motion of the shocks are not properly tuned, that the DSGE model enters in an explosive path, thus preventing the computation of impulse-response functions and the adoption of the model for policy analysis exercises.
Empirical issues
The second stream of problems concern the empirical validation of DSGE models. The estimation and testing of DSGE models are usually performed assuming that they represent the true data generating process (DGP) of the observed data (Canova 2008). This implies that the ensuing inference and policy experiments are valid only if the DSGE model mimics the unknown DGP of the data8.
As mentioned in Section 2, DSGE models can be represented as a VAR of the form:
| $$A_{0}(\phi)x_{t} = H_{1}(\phi)x_{t-1}+H_{2}({\phi})E_{t},$$ | (4) |
Following Fukac & Pagan (2006), the econometric performance of DSGE models can be assessed along the identification, estimation and evaluation dimensions. Before going in depth with this type of analysis, two preliminary potential sources of problems must be discussed. First, the number of endogenous variables contemplated by DSGE models is usually larger than the number of structural shocks. This problem may lead to stochastic singularity and it is typically solved by adding measurement errors or increasing the number of structural shocks (see Fernandez-Villaverde et al. 2016). Second, \(H_{1}\) and \(H_{2}\) are reduced rank matrixes. This problem is circumvented by integrating variables out of the VAR (eq. 4) as long as \(H_{1}\) and \(H_{2}\) become invertible. This process leads to a VARMA representation of the DSGE model. This is not an innocent transformation for two reasons: i) if the moving average component is not invertible, the DSGE model cannot have a VAR representation; ii) even if the VAR representation of the DSGE model exists, it may require an infinite number of lags (more on that in Fernandez-Villaverde et al. 2005, 2016; Ravenna 2007; Alessi et al. 2007).
Identification. Given the large number of non-linearities present in the structural parameters (\(\theta\)), DSGE models are hard to identify (Canova 2008). This leads to a large number of identification problems, which can affect the parameter space either at the local or at the global level. A taxonomy of the most relevant identification problems can be found in Canova & Sala (2009)9. To sum them up: i) different DSGE models with different economic and policy implications could be observationally equivalent (i.e., they produce indistinguishable aggregate decision rules); ii) some DSGE models may be plagued by under or partial identification of their parameters (i.e., some parameters are not present in the aggregate decision rules or are present with a peculiar functional form); iii) some DSGE may be exposed to weak identification problems (i.e., the mapping between the coefficients of the aggregate decision rules and the structural parameters may be characterized by little curvature or by asymmetries), which could not even be solved by increasing the sample size.
Identification problems lead to biased and fragile estimates of some structural parameters and do not allow to rightly evaluate the significance of the estimated parameters applying standard asymptotic theories. This opens a ridge between the real and the DSGE DGPs, depriving parameter estimates of any economic meaning and making policy analysis exercises useless (Canova 2008). For instance, Schorfheide (2008) finds that the parameters of the New Keynesian Phillips curve estimated in 42 DSGE models published in academic journals range from zero to four. In most of the cases, identification problems can only be mitigated by appropriately re-parameterizing the model10.
Estimation. The identification problems discussed above partly affect the estimation of DGSE models. DSGE models are very hard to estimate by standard maximum likelihood (ML) methods, because ML estimator delivers biased and inconsistent results if the system is not a satisfying representation of the data. This turns out to be the case for DSGE models (see the evaluation section) and it helps to explain why ML estimates usually attain absurd values with no economic meaning and/or they are incompatible with a unique stable solution of the underlying DSGE model.
A strategy commonly employed when the DSGE model is estimated following the limited-information approach (cf. Section 2) consists in calibrating the parameters hard to identify and then estimating the others. Given the identification problems listed above, Canova (2008) argues that this strategy works only if the calibrated parameters are set to their "true" values. If this is not the case, estimation does not deliver correct results that can be used to address economic and policy questions (see also Canova & Sala 2009).
Bayesian methods apparently solve the estimation (and identification) problems by adding a prior function to the (log) likelihood function in order to increase the curvature of the latter and obtain a smoother function. However, this choice is not harmless: if the likelihood function is flat – and thus conveys little information about the structural parameters – the shape of the posterior distribution resembles the one of the prior, reducing estimation to a more sophisticated calibration procedure carried out on an interval instead on a point (see Canova 2008; Fukac & Pagan 2006). Unfortunately, the likelihood functions produced by most DSGE models are quite flat (see e.g. the exercises performed by Fukac & Pagan 2006). In this case, informal calibration is a more honest and internally consistent strategy to set up a model for policy analysis experiments (Canova 2008).
Evaluation. DSGE models should be capable to reproduce as many empirical stylized facts as possible. For instance, following Fukac & Pagan (2006), one can check: i) whether variables with deterministic trend cotrend; ii) whether I(1) variables co-integrate and the resulting co-integrating vectors are those predicted by the model; iii) the consistency (with respect to data) of the dynamic responses (e.g., autocorrelation, bivariate correlations); iv) the consistency of the covariance matrix of the reduced form errors with the one found in the data; v) the discrepancies between the time series generated by the model and real-world ones. In light of the Great Recession, the last point is particularly important: can DSGE models jointly account for the occurrence of mild and deep downturns (Stiglitz 2015)?
Fukac & Pagan (2006) perform such exercises on a popular DSGE model. First, they find that co-trending behaviors cannot be assessed because data are demeaned (a practice commonly followed by DSGE modelers). However, the computation of the technology growth rates compatible with the observed output growth rates shows that the possibility of technical regress is very high. Second, there are no co-integrating vectors, because output is the only I(1) variable. Third, the model is not able to successfully reproduce the mean, standard deviations, autocorrelations, bivariate correlations observed in real data. In addition, the DSGE model predicts the constancy of some "great" ratios (in line with the presence of a steady state of the economy), but this is not confirmed by real data. For instance, Fernandez-Villaverde et al. (2016) find a discrepancy between U.S. and DSGE-generated data, as DSGE models are not able to catch the increasing upward trend in the consumption-output ratio and the falling labor share. Fourth, many o -diagonal correlations implied by the covariance matrix of the errors are significantly different from zero, contradicting the DSGE model assumption of uncorrelated shocks. Fifth, the tracking performance of the model depends heavily on the assumed high serial correlation of the shocks.
Recent empirical evidence has found that non-linearities in the economic system can lead to different impact of macroeconomic policies according to the state of the economy (see e.g. Auerbach & Gorodnichenko 2012) and financial markets (Mittnik & Semmler 2013; Ferraresi et al. 2014). In DSGE models, the effects of monetary and fiscal policies are time invariant, even if the economy is trapped in a depression. More generally, DSGE models can do well in "normal" time, but they cannot account for crises and deep downturns (Stiglitz 2015), as well as for the size and duration of recessions (Ormerod 2004, 2010). This is not surprising since macroeconomic time series distributions are well approximated by fat tail densities (Fagiolo et al. 2008) and DSGE models typically assume Gaussian distributed shocks11. Moreover, Ascari et al. (2015) find that even fat-tailed Laplace shocks are assumed, the distributions of the time series generated by DSGE models have much thinner tails than those observed in real data. The propagation mechanism of DSGE models appears to work in the wrong direction, smoothing instead of magnifying shocks.
The results just described seem to support Favero (2007) in claiming that modern DSGE models are exposed to the same criticisms advanced against the old-fashioned macroeconometric models belonging to the Cowles Commission tradition: they pay too much attention to the identification of the structural model (with all the problems described above) without testing the potential misspecification of the underlying statistical model (see also Johansen 2006; Juselius & Franchi 2007)12. In DSGE models, "restrictions are made fuzzy by imposing a distribution on them and then the relevant question becomes what is the amount of uncertainty that we have to add to model based restrictions in order to make them compatible not with the data but with a model-derived unrestricted VAR representation of the data" (Favero 2007, p. 29). If the statistical model is misspecified, policy analysis exercises loose significance, because they are carried out in a "virtual" world whose DGP is different from the one underlying observed time-series data.
More generally, the typical assertion made by DSGE modelers that their theoretical frameworks are able to replicate real world evidence seems at odds with a careful scrutiny of how empirical evaluation of DSGE models is really done. DSGE modelers, indeed, typically select ex-ante the set of empirical criteria that their models should satisfy in such a way to be sure that these restrictions are met. However, they usually restrain from confronting their models with the wealth of fundamental features of growth over the capitalist business cycle, which DSGE are not structurally able to replicate.
Political-economy issues
Given the theoretical problems and the puny empirical performance of DSGE models, one cannot accept the principles of the positive economics approach summarized by the "as if" argument of Milton Friedman (1953). The assumptions of DSGE models can no longer be defended invoking arguments such as parsimonious modeling or data matching. This opens a Pandora’s box as one should study how the legion of assumptions of DSGE models affect their policy conclusions.
DSGE models presume a very peculiar framework, where representative agents endowed with rational expectations (RE) take rational decisions by solving dynamic programming problems. This implies that: i) agents perfectly know the model of the economy; ii) agents are able to understand and solve every problem they face without making any mistakes; iii) agents know that all other agents behave according to the first two points. In practice, agents are endowed with a sort of "Olympic" rationality and have free access to the whole information set13.
Rational expectation is the short-cut employed by DSGE model to deal with uncertainty. Such strong assumption rises many issues14. First, rational expectations are a property of the economic system as a whole, individual rationality is not a sufficient condition for letting the system converge to the RE fixed-point equilibrium (Howitt 2011). Moreover, it is unreasonable to assume that agents possess all the information required to attain the equilibrium of the whole economy (Caballero 2010), especially in periods of strong structural transformation, like the Great Recession, that require policies never tried before (e.g. quantitative easing, see Stiglitz 2011, 2015). Agents can also have the "wrong" model of the economy and available data are not sufficient to refute it (see the seminal contribution of Woodford 1990, among the rich literature on sunspots). Hendry & Minzon (2010) point out that when "structural breaks" affect the underlying stochastic process that governs the evolution of the economy, the learning process of agents introduce further non-stationarity into the system, preventing the economy to reach an equilibrium state. In such a framework, predictors grounded on robust devices performs better. More generally, in presence of Knightian uncertainty (Knight 1921; Keynes 1936, 1937), "rational" agents should follow heuristics as they always outperform more complex expectation formation rules (Gigerenzer 2007; Gigerenzer & Brighton 2009). Assuming that agents behaving according to what suggested by the psychological and sociological evidence allow then to build models which better account for macroeconomic phenomena (Akerlof 2002) including the current crisis (Akerlof & Shiller 2009). Finally, given such premises, no wonder that empirical tests usually reject the full-information, rational expectation hypothesis (see e.g. Guzman 2009; Coibion & Gorodnichenko 2011; Gennaioli et al. 2015).
The representative-agent (RA) assumption prevent DSGE models to address distributional issues, which are one of the major cause of the Great Recession and they are fundamental for studying the effects of policies. Indeed, increasing income (Atkinson et al. 2011) and wealth (Piketty & Zucman 2014) inequalities induced households to indebt more and more over time paving the way to the subprime mortgage crisis (Fitoussi & Saraceno 2010; Stiglitz 2011). In this framework, redistribution matters and different policies have a different impact on the economy according to the groups of people they are designed for (e.g. unemployed benefits have large multipliers than tax cuts for high-income individuals, see Stiglitz 2011). The study of redistributive policies require then models with heterogeneous not representative agents.
The RA assumption coupled with the implicit presence of a Walrasian auctioneer, which sets prices before exchanges take place, rule out almost by definition the possibility of interactions carried out by heterogeneous individuals. This prevents DSGE model to study the dynamics of credit and financial markets accurately. Indeed, the assumption that the representative agent always satisfies the transversality condition, removes the default risk from DSGE models (Goodhart 2009). Therefore, agents face the same interest rate (no risk premia) and all transactions can be undertaken in capital markets without the need of banks15. The abstraction from default risks does not allow DSGE models to contemplate the conflict between price and financial stability that Central Banks always face (Howitt 2011): they just care about the nth-order distortions caused by price misalignments which can eventually result in inflation without considering the huge costs of financial crisis (Stiglitz 2011, 2015). No surprise that DSGE models work fine in normal time but they are unequipped not only to forecast but also to explain the current crisis (Goodhart 2009; Krugman 2011).
In the same vein, DSGE models are not able to account for involuntary unemployment. Indeed, even if they are developed to study the welfare effects of macroeconomic policies, unemployment is not present or it only stems from frictions in the labor market or wage rigidities. Such explanations are especially hard to believe during deep downturns like e.g. the Great Recession. In DSGE models, the lack of heterogeneous, interacting firms and workers/consumers prevents to study the emergence of coordination failures (Cooper & John 1988), which could lead to an insufficient level of aggregate demand and to involuntary unemployment.
The "as if" methodology implies that the macroeconomics of DSGE models does not seem to be truly grounded on microeconomics (Stiglitz 2011, 2015). For instance, DSGE models do not take into account the micro and macro implications of imperfect information. Moreover, the behavior of agents is often described with arbitrary specification of the functional forms. The common employed (Dixit & Stiglitz 1977) utility function provides a bad description of agents’ behavior toward risk. Similarly, the Cobb-Douglas production function is not suited for studying income distribution issues.
More generally, within the Neoclassical-DSGE paradigm there is a sort of internal contradiction. On the one hand, strong assumptions such as rational expectations, perfect information and complete financial markets are introduced ex-ante to provide a rigorous and formal mathematical treatment of the problems and to allow for policy recommendations. On the other hand, many imperfections (e.g., sticky prices, rule-of-thumb consumers) are introduced ex-post without any theoretical justification only to allow DSGE model to match the data. This process is far from being innocuous: Chari et al. (2009) point out that the high level of arbitrariness of DSGE models in the specifications of structural shocks may leave them exposed to the Lucas critiques, preventing them to be usefully employed for policy analysis. Adopting less stringent – but in tune with the microeconomic statistical evidence – assumptions may contribute to jointly solve many empirical puzzles without introducing an army of ad-hoc imperfections.
Another possible issue concerns how business cycles arise in the DSGE framework. More specifically, the theory of business cycles embedded in DSGE models is exogenous: the economy rests in the steady state unless it is hit by a stream of exogenous stochastic shocks. As a consequence, DSGE models do not explain business cycles, preferring instead to generate them with a sort of deus-ex-machina mechanism. This could explain why even in normal times DSGE models are not able to match many business cycle stylized facts or have to assume serially correlated shocks to produce fluctuations resembling the ones observed in reality (cf. Zarnowitz 1985, 1997; Cogley & Nason 1993; Fukac & Pagan 2006). Even worse, the subprime mortgage crisis clearly shows how bubbles and, more generally, endogenously generated shocks are far more important for understanding economic fluctuations (Stiglitz 2011, 2015). How policymakers can assess the impact of policies in models not explaining business cycles is an open issue. For instance, the Great Recession revealed that the FED’s doctrine about cleaning up afterward asset bubbles bursts was patently wrong.
Moving to the normative side, one supposed advantage of the DSGE approach is the possibility to derive optimal policy rules. However, policymakers adopting optimal policy rules face certain costs – the strict assumptions at the root of DSGE models – but uncertain benefits. As argued by Galí (2008), optimal monetary policy rules cannot be used in practice, because they require the knowledge of the "true" model of the economy, the exact value of every parameter, and the real time value of every shocks. Moreover, when the "true" model of the economy and the appropriate loss function are not know, rule-of-thumb policy rules can perform better than optimal policy rules (Brock et al. 2007; Orphanides & Williams 2008). Indeed, in complex worlds with pervasive uncertainty (e.g. financial markets), regulation should be simple (Haldane 2012).
Recent Developments in DSGE Modeling: Patches or New Clothes?
The failure of DSGE models to account for the Great Recessions sparked new research avenues, which were also partly trying to address the critiques we reported inSection 3. More specifically, researchers in the DSGE camp have tried to include a financial sector to the barebone model, consider agents’ heterogeneity and bounded rationality, and explore the impact of rare shocks on the performance of DSGE models. In this Section, we provide a bird’s eye view of such recent developments.
The new generation of DSGE model with financial frictions are mostly grounded on the financial accelerator framework (Bernanke et al. 1999), which provides a straightforward explanation why credit and financial markets can affect real economic activity. The presence of imperfect information between borrowers and lenders introduces a wedge between the cost of credit and those of internal finance. In turn, the balance-sheets of lenders and borrowers can affect credit and the real sector via the supply of credit and the spread on loan interest rates (see Gertler & Kiyotaki 2010, for a survey). In Curdia & Woodford (2010), the presence of both patient and impatient consumers justify the existence of a stylized financial intermediary, which copes with default risk charging a spread on its loan subject to exogenous, stochastic disturbances. They find that optimal monetary policy does not change and the Central Bank should keep on controlling the short-term interest rate (see also Curdia & Woodford 2015). In the model of Gertler & Karadi (2011), households can be (randomly) workers or bankers. In the latter case, they provide credit to firms, but as they are constrained by deposits and the resources they can raise in the interbank market, a spread emerges between loan and deposits interest rates (see Christiano et al. 2011, 2013, for a similar framework where interest rate spread arises from exogenous firms’ failure risk). They find that during crises, unconventional monetary policy (i.e. Central Bank providing credit intermediation) is welfare enhancing (see also Curdia and Woodoford 2011; and Gertler and Kiyotaki, 2010 for an extended analysis of credit policies)16.
The foregoing papers allow for some form of mild heterogeneity among agents. The introduction of two types of agents allow DSGE models to explore new issues such as debt deflations or inequality (most of DSGE models with heterogeneous agents are grounded on Krusel and Smith 1998). For instance, Eggertsson & Krugman (2012) introduce patient and impatient agents and expose the latter to exogenous debt limit shocks, which force them to deleverage. They find that the model can account for Fisher debt deflations, liquidity traps, and support expansionary fiscal policies, as multipliers can be higher than one. Kumhof et al. (2015) study the link between rising inequality, household leverage and financial crises employing a DSGE model where top earner house-holds (5% of the income distribution) lend to the bottom ones (95% of the income distribution). They show that an exogenous inequality shock induces low-income households to increase their indebtedness, raising their rational willingness to default and, in turn, the probability of a financial crisis.
An increasing number of DSGE models allow for various forms of bounded rationality (see Dilaver et al. 2016, for a survey). In one stream of literature, agents know the equilibrium of the economy and form their expectations as if they were econometricians, by using the available observation to compute their parameter estimates via ordinary least square (the seminal contribution is Evans and Honkapohja 2001; see also Deak et al. 2015, for a DSGE model with individual rationaltiy). Building on the Brock & Hommes (1997), in an increasing number of DSGE models (see e.g. Branch & McGough 2011; De Grauwe 2012; Anufriev et al. 2013; Massaro 2013), agents can form their expectations using an ecology of different learning rules (usually fundamentalist vs. extrapolative rules). As the fraction of agents following different expectations rules change over time, "small" shocks can give raise to persistent and asymmetric fluctuations and endogenous business cycles may arise17.
Finally, a new generation of DSGE models try to account for deep downturns and disasters. Curdia et al. (2014) estimate the Smets & Wouters (2007) model assuming that Student’s t-distributed shocks. They find that the fit of the model improves and rare deep downturns are relevant (see also Fernandez-Villaverde & Levintal 2016, for a DSGE model with exogenous time-varying rare disaster risk). A similar strategy is employed to Canzoneri et al. (2016) to allow the effects of fiscal policies to change over time. By adding countercyclical exogenous bank intermediation costs to the Curdia & Woodford (2011) model, they obtain state-dependent fiscal multipliers, which can be abundantly higher than one in recessions.
Taking stock of new DSGE developments. The recent advances in DSGE models are impressive and seem to solve many of the problems mentioned in Section 3. Nevertheless, can they be truly considered real improvements in the DSGE research paradigm? We do think that the answer is negative.
Let us consider first DSGE models with financial frictions. They certainly performs better than standard DSGE models, but the way they introduce finance is completely ad-hoc resorting to exogenous shocks and pre-determined categories of agents (patient vs. impatient or random probability to become "banker"). In that, they just scratch the surface of the impact of credit and finance on real economic dynamics without explicitly modeling the behavior of banks (e.g. endogenous risk-taking), accounting for the role of network interactions, and studying the implications of endogenous money. Moreover, also DSGE models with financial frictions avoid to explicitly consider the interactions occurring among heterogeneous agents, which is a pervasive feature of credit (and real) markets.
The same critiques can be applied to the other streams of research. Every time heterogeneity is taken into account, there are two types of agents exogenously determined (e.g. rich and poor), facing exogenous shocks and no possibilities of interactions. DSGE models can now encompass both mild and deep downturns, but they only assume them, increasing the degrees of freedom of the models. Indeed, business cycles are still triggered by exogenous shocks, which come from a fat-tailed distribution or they have massive negative effects18. When bounded rationality is present, agents can be either rational or non-rational or, in alternative, they estimate the parameters of the shared model of the economy. In the latter case, interactions is not relevant, while in the first case, it affects the dynamics of the economy only indirectly via the evolving proportion of agents adopting different expectation rules.
In light of the foregoing discussion, we think that the new developments in DSGE camp are certainly welcome, but they are just patches added to torn clothes. The relevant question then is: How many patches can one add before trashing it? For instance, Lindé et al. (2016), after having expanded the benchmark DSGE model to account for the zero-lower bound, non-Gaussian shocks, and the financial accelerator, conclude that such ex-tensions "do not suffice to address some of the major policy challenges associated with the use of non-standard monetary policy and macroprudential policies"19. We do think that the emperor has no clothes, and macroeconomics should be grounded on the recent developments in complexity science. In that, agent-based computational economics (ACE) (Tesfatsion & Judd 2006; LeBaron & Tesfatsion 2008; Farmer & Foley 2009) represents a valuable tool. We present the ACE paradigm in the next section.
Agent-Based Models and Economic Policy
From DSGE to agent-based models
Given the theoretical and empirical problems of DSGE models discussed above, the positive economics approach advocated by Milton Friedman would suggest to remove or change the plethora of underlying assumptions in order to improve the performance of the model.
This recommendation is reinforced by two related observations. First, the assumptions underlying DSGE models become a sort of strait jacket that preclude the model to be flexible enough to allow for generalizations and extensions. Second, the unrealism of these assumptions prevent policymakers to fully trust the policy prescriptions developed with DSGE models.
It is far from clear why within the mainstream DSGE paradigm there is a widespread conservative attitude with no significant attempts to substitute the "Holy Trinity" assumptions of rationality, greed and equilibrium (Colander 2005) with more realistic ones. For instance, Akerlof (2007) argues that a broader definition of agents’ preferences which take into account the presence of realistic norms can violate many neutrality results of neoclassical economics without recurring to imperfections. Moreover, introducing heterogeneous agents or substituting the rationality assumption with insights coming from behavioral economics could substantially change the working of DSGE models. This position is also advocated in a recent work by Sinitskaya & Tesfatsion (2015), who explore models where economic agents are "locally constructive", that is they are constrained by their interaction networks, information, beliefs, and physical states when making decisions.
In any case, if neoclassical economists truly enlist themselves among those advocating an instrumentalist approach to scientific research, they should agree that when models display estimation and validation (descriptive) problems such as those exhibited by DSGE ones, the only way out would be to modify the models’ assumptions. As Wren-Lewis (2016) argues, the neo-classical revolution, which ultimately paved the way to the development of DSGE models, was mainly based on ideas and not events. In other words, he argues that models based on mainstream economics "focus on explaining only partial properties of the data" and share "an obsession with internal consistency", which "comes straight from the methodology". Given this lack of attention to explaining the events, experimenting with alternative sets of assumptions, supported by empirical data and experimental evidence, would be the recommendation that an instrumentalist researcher itself would pro-vide. A fortiori, this should become an urgent research project to pursue if, in addition, the model, as happens in the DSGE case, would also display problems on the normative side.
This is exactly the research avenue that a growing number of scholars have been pursuing in the last two decades. Dissatisfied with standard macroeconomic, micro-founded, general- equilibrium-based neoclassical models like those discussed above, they have begun to devise an entirely new paradigm labeled as "Agent-Based Computational Economics" (ACE). The philosophical underpinnings of ACE largely overlap with those of similar, complementary, approaches known in the literature as "Post Walrasian Macroeconomics" (Colander 2006b) and "Evolutionary Economics" (Nelson & Winter 1982; Dosi & Nelson 1994). The overlap is often so strong that one might safely speak of an emerging "heterodox synthesis". Such a large supply of heterodox models is exactly the basin which Setterfield (2016) argues central bankers and policy makers should draw from, in order to "entertain more eclectic views of how the economy functions".
The basic exercise ACE tries to perform is building models based on more realistic assumptions as far as agent behaviors and interactions are concerned, where more realistic here means rooted in empirical and experimental micro-economic evidence (Kirman 2016). For example, following the body of evidence provided by cognitive psychologists (see for example, among a vast literature, Kahneman & Tversky 2000; Gigerenzer 2007; Gigerenzer & Brighton 2009), the assumptions of perfect rationality and foresight are replaced with those of bounded rationality and adaptive behavior. More generally, ACE scholars share the view that agents in the model should have "the same information as do the economists modeling the economy" (Colander 2006a, p. 11). Similarly, insights from network theory (e.g., Albert & Barabasi 2002) and social interactions (e.g., Brock & Durlauf 2001) suggest to move away from the unrealistic and oversimplifying assumptions concerning agents interactions typically employed in neoclassical models and allow for direct, non-trivial interaction patterns. Finally, the widespread evidence on persistent heterogeneity and turbulence characterizing markets and economies indicate to abandon crazy simplifications such as the representative agent assumption, as well as the presumption that economic systems are (and must be observed) in equilibrium, and to focus instead on out-of-equilibrium dynamics endogenously fueled by the interactions among heterogeneous agents.
In other words, ACE can be defined as the computational study of economies thought as complex evolving systems (Tesfatsion 2006a). Notice that neoclassical economics, on the contrary, typically deals with economies conceived as simple, linear, homogeneous and stationary worlds. It should not come as a surprise that the class of models used by ACE to explore the properties of markets, industries and economies (called agent-based models, ABMs) are far more complicated – and harder to analyze – objects than their neoclassical counterparts. In the following Section, we will therefore begin by outlying the basic building blocks of ABMs. Next, we will address the question how ABMs can be employed to deliver normative implications. Then, we will briefly review some examples of policy exercises in ABMs. Some final remarks about pro and cons of using ABMs for policy analysis will be left for the concluding section.
Building blocks of ABMs
The last two decades have seen a rapid growth of agent-based modeling in economics. An exhaustive survey of this vast literature is of course beyond the scope of this work20. However, before proceeding, it is useful to introduce the main ten ingredients that tend to characterize economic AB models.
- A bottom-up perspective. A satisfactory account of a decentralized economy is to be addressed using a bottom-up perspective. In other words, aggregate properties must be obtained as the macro outcome of a possibly unconstrained micro dynamics going on at the level basic entities (agents). This contrasts with the top-down nature of traditional neoclassical models, where the bottom level typically comprises a representative individual and is constrained by strong consistency requirements associated with equilibrium and hyper-rationality.
- Heterogeneity. Agents are (or might be) heterogeneous in almost all their characteristics.
- The evolving complex system (ECS) approach. Agents live in complex systems that evolve through time. Therefore, aggregate properties are thought to emerge out of repeated interactions among simple entities, rather than from the consistency requirements of rationality and equilibrium imposed by the modeler.
- Non-linearity. The interactions that occur in AB models are inherently non-linear. Additionally, non-linear feedback loops exist between micro and macro levels.
- Direct (endogenous) interactions. Agents interact directly. The decisions undertaken today by an agent directly depend, through adaptive expectations, on the past choices made by other agents in the population.
- Bounded rationality. The environment in which real-world economic agents live is too complex for hyper-rationality to be a viable simplifying assumption. It is suggested that one can, at most, impute to agents some local and partial (both in time and space) principles of rationality (e.g., myopic optimization rules). More generally, agents are assumed to behave as boundedly rational entities with adaptive expectations.
- The nature of learning. Agents in AB models engage in the open-ended search of dynamically changing environments. This is due to both the ongoing introduction of novelty and the generation of new patterns of behavior; but also on the complexity of the interactions between heterogeneous agents (see point 5 above).
- "True" dynamics. Partly as a consequence of adaptive expectations (i.e., agents observe the past and form expectations about the future on the basis of the past), AB models are characterized by true, non-reversible, dynamics: the state of the system evolves in a path-dependent manner21.
- Endogenous and persistent novelty. Socio-economic systems are inherently non-stationary. There is the ongoing introduction of novelty in economic systems and the generation of new patterns of behavior, which are themselves a force for learning and adaptation. Hence, agents face "true (Knightian) uncer-tainty" (Knight 1921) and are only able to partially form expectations on, for instance, technological out-comes.
- Selection-based market mechanisms. Agents typically undergo a selection mechanism. For example, the goods and services produced by competing firms are selected by consumers. The selection criteria that are used may themselves be complex and span a number of dimensions.
The basic structure of ABMs
Models based on (all or a subset of) the ten main ingredients discussed above typically possess the following structure. There is a population – or a set of populations – of agents (e.g., consumers, firms, etc.), possibly hierarchically organized, whose size may change or not in time. The evolution of the system is observed in discrete time steps, \(t=1,2,\dots\). Time steps may be days, quarters, years, etc.. At each \(t\), every agent \(i\) is characterized by a finite number of micro-economic variables \(\underline{x}_{i,t}\) (which may change across time) and by a vector of micro-economic parameters \(\underline{\theta}_i\) (that are fixed in the time horizon under study). In turn, the economy may be characterized by some macroeconomic (fixed) parameters \(\Theta\).
Given some initial conditions \(\underline{x}_{i,0}\) and a choice for micro and macro parameters, at each time step \(t>0\), one or more agents are chosen to update their micro-economic variables. This may happen randomly or can be triggered by the state of the system itself. Agents selected to perform the updating stage collect their available information about the current and past state (i.e., micro-economic variables) of a subset of other agents, typically those they directly interact with. They plug their knowledge about their local environment, as well as the (limited) information they can gather about the state of the whole economy, into heuristics, routines, and other algorithmic, not necessarily optimizing, behavioral rules. These rules, as well as interaction patterns, are designed so as to mimic empirical and experimental knowledge that the researcher may have collected from his/her preliminary studies.
After the updating round has taken place, a new set of micro-economic variables is fed into the economy for the next-step iteration: aggregate variables \(\underline{X}_t\) are computed by simply summing up or averaging individual characteristics. Once again, the definitions of aggregate variables closely follow those of statistical aggregates (i.e., GDP, unemployment, etc.).
The stochastic components possibly present in decision rules, expectations, and interactions will in turn imply that the dynamics of micro and macro variables can be described by some (Markovian) stochastic processes parameterized by micro- and macro-parameters. Hoverer, non-linearities which are typically present in decision rules and interactions make it hard to analytically derive laws of motion, kernel distributions, time-\(t\) probability distributions, etc. for the stochastic processes governing the evolution of micro and macro variables.
This suggests that the researcher must often resort to computer simulations in order to analyze the behavior of the ABM at hand. Note that in some simple cases such systems allow for analytical solutions of some kind. Needless to say, the more one injects into the model assumptions sharing the philosophy of the building blocks discussed above (cf. Section 5), the less tractable turns out to be the model, and the more one needs to resort to computer simulations. Simulations must be intended here in a truly constructive way, e.g. to build and "grow" a society "from the bottom up", in the spirit of object-oriented programming.
Descriptive analysis of ABMs
When studying the outcomes of ABMs, the researcher often faces the problem that the economy he/she is modeling is by definition out-of-equilibrium. The focus is seldom on static equilibria or steady-state paths. Rather, the researcher must more often look for long-run statistical equilibria and/or emergent properties of aggregate dynamics (that is, transient statistical features that last sufficiently long to be observed and considered stable as compared to the time horizon of the model; see Lane 1993, for an introduction). Such an exploration is by definition very complicated and it is made even more difficult by the fact that the researcher does not even know in advance whether the stochastic process described by its ABM is ergodic or not and, if it somehow converges, how much time will take for the behavior to become sufficiently stable.
Suppose for a moment that the modeler knows, e.g., from a preliminary simulation study or from some ex-ante knowledge coming from the particular structure of the ABM under study, that the dynamic behavior of the system becomes sufficiently stable after some time horizon \(T^{\ast}\) for (almost all) points of the parameter space. Then a possible procedure that can be implemented to study the output of the ABM runs as the one synthetically depicted in Figure 1.
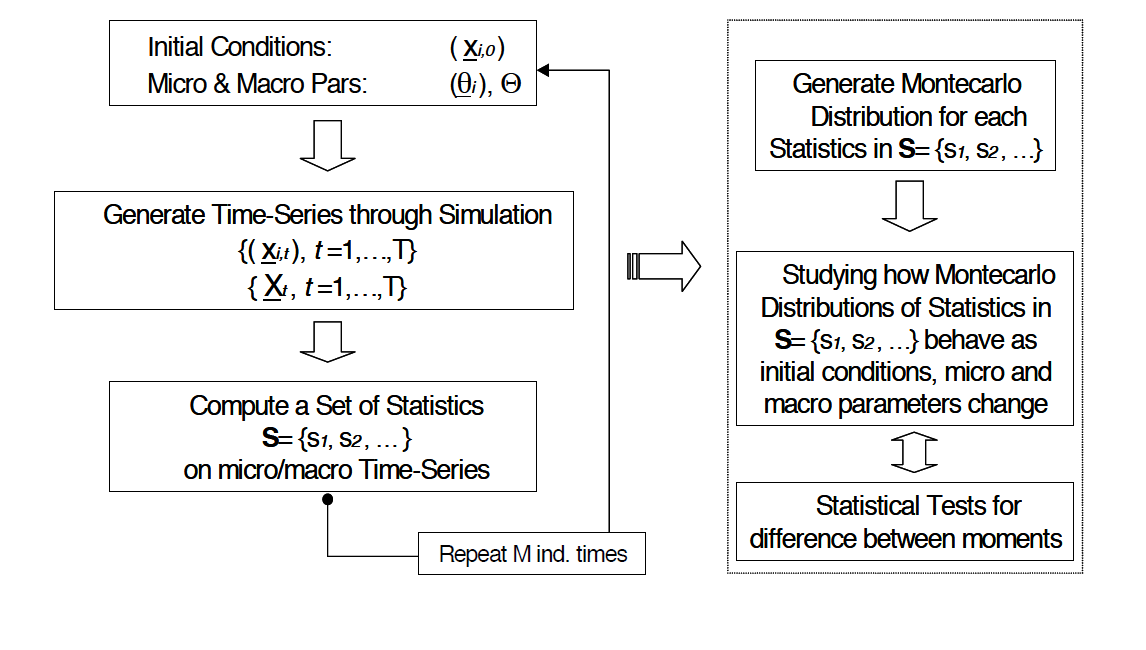
Given some choice for initial conditions, micro and macro parameters, assume to run our system until it relaxes to some stable behavior (i.e., for at least \(T>T^{\ast}\) time steps). Suppose we are interested in a set \(S=\{s_1,s_2,\dots\}\) of statistics to be computed on micro and macro simulated variables. For any given run the program will output a value for each statistic. Given the stochastic nature of the process, each run will output a different value for the statistics. Therefore, after having produced \(M\) independent runs, one has a distribution for each statistic containing \(M\) observations, which can be summarized by computing its moments.
Recall, however, that moments will depend on the choice made for initial conditions and parameters. By exploring a sufficiently large number of points in the space where initial conditions and parameters are allowed to vary, computing the moments of the statistics of interest at each point, and by assessing how moments do depend on parameters, one might get a quite deep descriptive knowledge of the behavior of the system (see Figure 1).
So far, we have naively assumed that the DGP described by the ABM under study is ergodic and stationary. However, is it possible to check this assumption quantitatively? Recent research indeed provides alternatives to the researcher interested in statistically assessing such an issue, and therefore better understand the behavior of the model, and draw inferences about the real system it is intended to represent (Richiardi et al. 2006). As an example, Grazzini (2012) discusses the use of Wald-Wolfowitz tests applied to ABMs and shows that, under appropriate settings, these procedures can detect non-stationarity and non-ergodicity.
Model selection and empirical validation
From the foregoing discussion, it clearly emerges that in agent-based modeling (as in many other modeling endeavors) one often faces a trade-off between descriptive accuracy and explanatory power of the model. The more one tries to inject into the model "realist" assumptions, the more the system becomes complicated to study and the less clear the causal relations going from assumptions to implications are. ABM researchers are well aware of this problem and have been trying to develop strategies to guide the process of assumption selection. For example, one can try to solve the trade-off between descriptive capability and explanatory power either by beginning with the most simple model and complicate it step-by-step (i.e., the so-called KISS strategy, an acronym standing for "Keep It Simple, Stupid!") or by starting with the most descriptive model and simplify it as much as possible (i.e., the so-called KIDS strategy, "Keep It Descriptive, Stupid!"). A third, alternative strategy prescribes instead to start with an existing model and successively complicate it with incremental additions (this strategy might be labeled TAPAS, which stands for "Take A Previous model and Add Something").
In all these procedures, the extent to which the ABM is able to empirically replicate existing reality should play a crucial role in discriminating the point at which any procedure should stop22.
Notice that the very structure of ABMs naturally allows one to take the model to the data and validate it against observed real-world observations. Indeed, an ABM can be thought to provide a DGP, which we think real-world observations being a realization of. More precisely, let us suppose that we believe that observed data are generated by an unknown (to us) colossal DGP, with an almost infinite number of parameters, which we can label as real-world DGP (rwDGP). Suppose further that such rwDGP can be broken in reasonable smaller weakly-exogenous components, each one with a reasonable number of parameters, and each one describing a small set of variables that we are interested in, on the basis of a small set of other variables. Building an ABM means attempting to approximate one of those small rwDGPs. Due to its stochastic structure, an ABM actually mimics the small rwDGP we are studying by a theoretical DGP that generates the same variables each time we run the model. Of course, we only have one observation generated by the rwDGP, and this makes any inference very difficult (but this has to do with another story, which philosophers call the problem of induction. . . ).
Many approaches to empirical validation (and selection) of ABMs can be in principle taken, and the debate is very open here23.
For example, one might select among ABMs (and within different parameter setups of the same ABM) with respect to the number of stylized facts each of them is able to jointly replicate. A typical procedure to be followed starts with asking whether a particular model can simultaneously reproduce some set of stylized facts for a given parametrization (a sort of "exercise in plausibility"); then explore what happens when the parameter setup changes; finally, investigate if some meaningful causal explanation can be derived out of that step-by-step analysis. This approach has been recently criticized, in that it is not able to identify the correct causal structures that may have generated the observed evidence. Indeed, as argued by Guerini & Moneta (2016a), many alternative causal structures can underlie the set of statistical dependencies observed in the data. To attempt to over-come this issue, Guerini & Moneta (2016b) propose, firstly, to estimate the causal structure incorporated in the model using its simulated outputs, and then comparing it with the causal structure detected in the real-world data that the model aspires to replicate. Both causal structures are derived from fitting vector autoregression models, estimated using both artificial and real-world data by means of causal search algorithms.
Alternatively, one can first select among parameters by calibrating the model (e.g., by directly estimate parameters, when possible, with micro or macro data) and then judge to which extent the calibrated model is able to reproduce the stylized facts of interest. A recent stream of literature tries to pursue this idea and recover the parameters of ABMs using some form of parameter estimation (or calibration). For example, Gilli & Winker (2003), Alfarano et al. (2005), Winker et al. (2007), Grazzini et al. (2013) employ different blends of indirect estimation methods, whereas Grazzini & Richiardi (2015) propose to estimate parameters of ergodic ABMs using simulated minimum distance. Note that this latter technique has the merit of being potentially applicable to both the long-run equilibria of the model and during adjustment phases. Conversely, Recchioni et al. (2015) approach the problem of calibrating the free parameters of ABMs as a nonlinear constrained optimization, which can be solved numerically via gradient-based methods, whereas Fabretti (2012) employs search technologies coming from genetic algorithms to explore the space of all possible parameter combinations in simple ABMs of financial markets. More recently, Grazzini et al. (2015) have suggested a Bayesian inference approach, as opposed to simulated minimum distance, to estimate ABM parameters, whereas Lamperti (2015, 2016) resorts to information-criteria techniques to quantify the distance between the true probabilistic dynamics of the output of the model and the data (to be minimized in order to achieve estimation), without needing to impose any stationarity requirements (see also Barde 2015).
Note that, unlike economists supporting the NNS approach — who hold strong theoretical priors rooted in the DSGE model — ACE scholars are more interested in developing plausible theories, which however are not dogmatically deemed to be the "correct" ones (on this point, see also Colander 2006a). Therefore, estimation and calibration of ABM parameters must not be intended as a way to identify their true, real-world values, but rather to single out ranges wherein true parameters could lie. In this respect, we note also that parameter estimation of ABMs may easily become not computationally viable, especially when the number of parameters to be estimated is large and data availability is scarce.
One of the problems related to all these validation exercises is rooted on their computational requirements. As discussed in Grazzini et al. (2015), the curse of dimensionality makes the practical application of the tools discussed insofar nearly impossible for medium and large scale ABMs. To address this problem, Lamperti et al. (2016b) have proposed to use machine learning surrogates to conveniently filter the parameter space of simulation models, dramatically reducing the computational effort needed to explore the behavior of the model when many parameters are at stake.
No matter the empirical validation procedure actually employed, its basic goal is often to restrict the size of the set of free parameters. In fact, over-parameterized models are difficult to interpret and analyze, because no one knows whether the same conclusions could have been obtained in a simpler, less parameterized model. Even if empirical validation allows one to restrict the set of free parameters to a reasonably-sized one, many methodological problems still remain when the model is used to perform policy experiments. If any parametrization represents an alternative world, which one should be employed to assess policy performance? What is the role of initial conditions? What kind of sensitivity analysis should be performed? Recent developments try to mitigate over-parameterization issues resorting to phase-diagrams (Gualdi et al. 2015), Kriging meta-modeling (Salle & Yıldızoğlu 2014; Dosi et al. 2016f; Bargigli et al. 2016), and machine-learning surrogates (2016b). We shall briefly come back to these issues in the concluding remarks.
Here, it is important to note that the methodological debate within the agent-based community is very lively. Among many interesting lines of methodological research, one of the most crucial ones concerns the issue of realism of the assumptions in economic models (for a more general appraisal, see Schlefer 2012). Indeed, whereas many ABM scholars argue that their approach allows for more realism in the way individual behaviors and interactions are accounted for in theoretical models (as opposed to neoclassical ones), others have maintained that ABM must as well trade o between successful model building and empirical accuracy of assumptions (Deichsel & Pyka 2009). Therefore, in order to provide ABMs that deliver meaningful statistical implications, agent-based researchers must often employ assumptions that are not the most descriptively accurate ones.
Policy experiments in ABMs: Some considerations
ABMs configure themselves as a very powerful device to address policy questions in more realistic, flexible and modular frameworks. Indeed, as far as economic policy is concerned, ABMs have many advantages as compared to neoclassical tools as the DSGE model, which we organize in what follows into two classes: theory and empirics.
Theory. ABMs, contrary to neoclassical ones, do not impose any strong theoretical consistency requirements (e.g., equilibrium, representative individual assumptions, rational expectations). This is because they are not required ex-ante to be analytically solvable. Such no-strait-jacket condition allows for an extremely higher flexibility in model building. If this is coupled with a serious empirical-validation requirement (see below), we are in presence of a semi-instrumentalist approach, where bad (but empirically-plausible) assumptions can be re-placed with better (and empirically-plausible) ones if the model does not perform as expected. Note also that in absence of strong consistency conditions, assumptions can be replaced in a modular way, without impairing the analysis of the model. Indeed, in standard neoclassical models one cannot simply replace the optimization assumption with another one just because the model does not behave well, as that would possibly destroy its analytical solvability. This is not so in ABMs: assumptions – or simply small elements of them – can be taken out of the shelf and easily implemented in the model thanks to the flexibility of computer programming languages.
Empirics. As discussed above, ABMs can be thought as generators of alternative worlds, i.e. theoretical DGPs that approximate the unknown one. Contrary to neoclassical models, the structure of ABMs allows to take them to the data more easily. This can be done in two ways. First, one can validate the inputs of ABMs, i.e. fine-tune modeling assumptions about individual behaviors and interactions to make them more similar to the observed ones. Second, one can validate the model on the output side, by e.g. restricting the space of parameters, individual behaviors and interactions, and initial conditions to those that allow the model to replicate the stylized facts of interest. This allows for a degree of realism that is much higher than that exhibited by e.g. DSGE models (Farmer & Foley 2009). Furthermore, thanks to the theoretical flexibility discussed above, agent-based models can target a rich ensemble of stylized facts at different level of aggregation (i.e. micro vs. macro regularities). More specifically, a macroeconomic agent-based models is typically able to replicate macroeconomic stylized facts such as endogenous growth and economic fluctuations, the emergence of banking crises and deep down-turns, relative volatilities and co-movements of macro aggregates at the business cycles frequencies. The same model can also jointly account for microeconomic stylized facts concerning firm size and growth rate distributions, firm productivity dynamics, firm investment patterns, wage and income inequality, etc. (for a detailed example of the empirical regularities reproduced by a macro ABM see Dosi et al. 2016b). This is a major advantage of ABMs vis-à-vis. DSGE ones, which are typically built – in order to retain analytical solvability – to explain only one or two single macro stylized facts (see the discussion in Aoki 2006, for more details), and cannot replicate by construction any micro empirical regularities given the representative-agent assumption.
But how can one actually conduct policy experiments in ABMs? In a very natural way, indeed. Take again the procedure for ABM descriptive analysis outlined in Figure 1. Recall that micro and macro parameters can be designed in such a way to mimic real-world key policy variables like tax rates, subsidies, interest rates, money, etc. and other key behavioral measures affecting individual incentives in growth, innovation or technologically-related policies. Moreover, initial conditions might play the role of initial endowments and therefore describe different distributional setups. In addition, interaction and behavioral rules employed by economic agents can be easily devised so as to represent alternative institutional, market or industry setups. Since all these elements can be freely interchanged, one can investigate a huge number of alternative policy experiments and rules, the consequences of which can be assessed either qualitatively or quantitatively (e.g., by running standard statistical tests on the distributions of the statistics in \(S\)). For example, one might statistically test whether the effect on the moments of the individual consumption distribution (average, etc.) will be changed (and if so by how much) by a percentage change in any given consumption tax rate. Most importantly, all this might be done while preserving the ability of the model to replicate existing macroeconomic stylized facts (e.g. some time-series properties of observed aggregate variables such as persistence of output growth-rate fluctuations, relative standard deviations, cross-correlations, etc.), as well as microeconomic empirical regularities (e.g. firm size distributions, firm productivity dynamics, firm investment patterns, etc.).
Macroeconomic Policy in ABMs: A Survey
The number of agent-based models dealing with policy issues is increasing fast over time24 and such a trend has received a new impulse after the Great Recession uncovered many weakness of DSGE models. This success is partly due to the fact that policy makers appear to be more and more willing to believe in results stemming from detailed simulation models (such as ABMs), where the underlying economic structure can be observed25, rather than in general insights produced by quite abstract mathematical models such as DSGE ones.
The number of ABMs addressing policy issues is becoming so large, that a survey of the whole literature would probably deserve a whole book rather than a paper. ABMs have indeed been employed in many different policy arenas such as industrial dynamics, market design, environmental regulation, traffic management, etc. We focus our attention on the subset of ABMs evaluating the impact of macroeconomic policies, which can be straightforwardly compared to DSGE models and can respond to the new theoretical and empirical challenges raised by the Great Recession. More specifically, in what follows we classify agent-based models in five areas, namely fiscal policy, monetary policy, macroprudential policy, labor market policy, and climate change policy.
Fiscal policy
The Great Recession has rewaked interest for employing fiscal policies to tackle economic downturns. An advantage of agent-based models vis-á-vis mainstream ones is the possibility to jointly study the short- and long-run impact of fiscal policies.
Dosi et al. (Dosi et al. 2010) try to do so developing an ABM, bridging Keynesian theories of demand-generation and Schumpeterian theories of technology-fueled economic growth (the \(K+S\) model; see Dosi et al. 2016b, for a survey). In the full-fledge version, the \(K+S\) model is populated by heterogeneous capital-good firms, consumption good-firms, consumers/workers, banks, Central Bank, and a public sector. Capital-good firms perform R&D and sell heterogeneous machine tools to consumption-good firms. Consumers supply labor to firms and fully consume the income they receive. Banks provide credit to consumption-good firms to finance their production and in-vestment decisions. The Central Bank fixes the short-run interest rate and the government levies taxes and it provides unemployment benefits. The model is able to endogenously generate growth and jointly account for mild recessions and deep downturns. Moreover, it is able to replicate an ensemble of stylized facts concerning both macroeconomic dynamics (e.g. cross-correlations, relative volatilities, output distributions) and microeconomic ones (firm size distributions, firm productivity dynamics, firm investment patterns). After having been empirically validated according to the output generated, the K+S model is employed to study the impact of fiscal policies (i.e. tax rate and unemployment benefits) on average GDP growth rate, output volatility and unemployment rate. The authors find that Keynesian fiscal policies are a necessary condition for economic growth and they can be successfully employed to dampen economic fluctuations26. Moreover, Dosi et al. (Dosi et al. 2013) find a strong interaction between income distribution and fiscal policies: the more income distribution is skewed toward profits, the greater the case for fiscal policies to dampen macroeconomic fragility27.
Different fiscal austerity policies are studied in Dosi et al. (2015). They find that fiscal consolidation rules are "self-defeating", as they depress the economy without improving public finances. Similar conclusions are reached by Teglio et al. (2015) employing the EURACE model (Cincotti et al. 2012b). Moreover, the negative effects of fiscal policies are magnified by higher level of income inequality Dosi et al. 2015). Finally, austerity policies can also reduce long-run productivity and GDP growth, by harming innovation rate and the diffusion of new technologies (Dosi et al. 2016c) and firms’ investment rates (Bassi & Lang 2016). In fact, stabilization policies can affect both short- and long-run dynamics as found also by Russo et al. (2007) and Harting (2015).
A series of agent-based models explore the interactions between financial instability and fiscal policies. Napoletano et al. (2015) build an agent-based model populated by heterogeneous households facing time-varying credit constraints. They find that deficit-spending fiscal policy dampens the magnitude and persistence of bankruptcy shocks. Moreover, the size of the multipliers change over time and it is related to the evolution of credit rationing. Chiarella & Di Guilmi (2012) explore the consequences of financial fragility from the firms’ perspective developing an agent-based model with Minskyan flavor where the investment of heterogeneous firms is conditioned by market expectations, money can either exogenous or endogenous and the Government can levy taxes on profits or private wealth. The model shows that with endogenous money and credit, a wealth tax is a more effective stabilization policy than a tax on profit. Relatedly, in an agent-based model with heterogeneous workers, firms, and banks interacting in markets through a decentralized matching protocol, Riccetti et al. (2014) find that during extend crises triggered by bank defaults and financial instability, the Government sector can stabilize the economy.
Finally, the impact of different expectation-formation mechanisms are studied in the K+S model by Dosi et al. (2016a). Starting from the Brock & Hommes (1997) framework, they find that austerity policies are self-defeating even when agents can switch among different expectation rules (e.g. adaptive, trend-follower expectations) as in Anufriev et al. (2013). Moreover, in line with Gigerenzer (2007) and Gigerenzer & Brighton (2009), they find that the performance of the economy does not improve when agents are more rational. On the contrary, when agents employ ordinary least square to form their forecasts, the individual and collective performance worsen, as structural breaks and Knightian uncertainty cannot be taken into account. Relatedly, Haber (2008) studies the interactions between different expectation-formation mechanisms and fiscal and monetary policies in an agent-based model. He finds that the introduction of more sophisticated expectations reduce the effects of fiscal policy, whereas it increases the impact of monetary policy.
Monetary policy
DSGE models have mostly dealt with monetary policy, searching for the best monetary rule. At the same time, the current Great Recession has revealed the importance of credit and financial markets and has showed that monetary policy alone is not sufficient to put economies back on their steady growth path. This has triggered novel research e orts in the DSGE camp as discussed in Section 4. At the same time, the emphasis of agent-based models on heterogeneity and interactions make them natural candidates to study the effects of monetary policies (and bank regulation, see below) in a framework characterized by financial fragility (e.g. Delli Gatti et al. 2005a; Dosi et al. 2013, 2015; Caiani et al. 2015), bankruptcy cascades (e.g. Delli Gatti et al. 2010; Battiston et al. 2012), deleveraging dynamics (e.g. Raberto et al. 2012; Seppecher & Salle 2015), etc.
A growing set of agent-based models employ Taylor rules to explore the effects of monetary policy on the economy. In this respect, such policy analyses exercises are similar to the ones conducted with DSGE models, but the complexity-rooted approach of ABM can bring fresh new insights.
The K+S model is employed by Dosi et al. (2015) to study the impact of a "conservative" Taylor rule focused only on inflation vis-à-vis a dual mandate one, which aim also at stabilizing the unemployment rate. They find that the dual-mandate Taylor rule is more efficient in stabilizing the economy (a similar result is found in Raberto et al. 2008; Delli Gatti & Desiderio 2015) without substantially increasing the inflation rate. However, the trans-mission channel is different from the traditional one employed by DSGE models grounded on the interest rate. Indeed, the presence of a credit channel implies that a dual-mandate monetary rule reduces the destabilizing effects of credit pro cyclicality, providing both banks and firms with a stronger financial record at the eve of recessions. More generally, there appears to be strong interactions not only between fiscal and monetary policies but also between macroprudential and monetary ones (more on that in Popoyan et al. 2015, and the papers discussed below). Finally, the effects of monetary policies become sharper as the level of income inequality increases (see also Dosi et al. 2013).
Alternative commitment vis-à-vis discretionary monetary strategies are studied in Delli Gatti et al. (2005b) in an economy populated by heterogeneous, interacting firms and workers. In the commitment strategy, the Central Bank employs a fixed parameter Taylor rule, whereas in the discretionary one, the parameters of the Taylor rule change according to a genetic algorithm, mimicking a learning process. They find that pervasive capital market imperfections imply that monetary policy affects the economy through the credit channel and that money is not neutral in the long-run. Moreover, the Taylor principle does not hold and the adaptive rule outperforms the commitment one according to the standard loss function criterion. Relatedly, Arifovic et al. (2010) study the time-inconsistency problem face by Central Banks in an ABM where the interaction between a boundedly-rational, evolutionary learning policy maker and a population of heterogeneous agents determines the actual inflation rate. The agents can either believe the inflation rate announced by the Central Bank or employ an adaptive learning scheme to forecast future inflation. Simulations show that the Central Bank learns to sustain an equilibrium with a positive, but fluctuating fraction of "believers" and that this outcome is Pareto superior to the equilibrium determined by standard models. Finally, Salle et al. (2013) study the performance of inflation targeting monetary policy in a model where heterogeneous agents (firms and consumers) adopt heuristics, but they continuously learn employing a genetic algorithm. They find that the credibility of the inflation target plays a major role in achieving the objectives of monetary policies, and the transparent communication of such a target by the Central Bank is instrumental to increase its credibility and in turn its ability to stabilize the economy. The foregoing conclusions are generalized in Salle (2015) with a model in which agents form their expectations according to artificial neural networks.
The effects of unconventional monetary policy are explored in Cincotti et al. (2010), who developed an ABM based on the EURACE platform to assess the effects of quantitative-easing monetary policy, in which the Central Bank finance government deficit buying treasury bonds. Simulation results show that the performance of the economy improves when expansionary fiscal policy and quantitative-easing monetary policy are implemented. However, such expansionary policies raise inflation and lead to higher output volatility in the long-run.
Arifovic & Maschek (2012) consider an open economy framework (see also Rengs & Wackerle 2014), where a Central Bank fixes the interest rate in order to try to avoid the emergence of a currency crisis, which is triggered by the (heterogeneous) devaluation expectations of investors, changing via a social evolutionary learning process. They find that decreasing the interest rates under the menace of a possible currency attack is more effective than defending the currency, as the latter policy increases the outflow of funds.
Financial instability, bank regulation and macroprudential policies
The Great Recession has not only revealed the importance of credit and financial markets for the real dynamics, but it has also uncovered the lack of research on the effects of macroprudential regulation and on its interactions with monetary policy (see e.g. Blanchard et al. 2013). Given their emphasis on heterogeneity and interactions, agent-based models are a natural tool to address such issues.
The role of loan-to-value ratios and static capital-adequacy regulation akin to the Basel II framework are studied in Ashraf et al. (2011), with an ABM where heterogeneous firms interact with banks providing them credit. Simulations of the model, calibrated to U.S data, show that during deep downturns bank credit can stabilize the economy, easing the entry of new firms and avoiding the bankruptcy of the incumbents. As consequence, less strict microprudential bank regulation (i.e. higher loan-to-value ratios and lower capital-adequacy ratios) allow the economy to recover faster from a crisis. Somewhat similarly, Dosi et al. (2013) find that in the bank-augmented K+S model, higher loan-to-value ratios positively affect macroeconomic growth when firms can rely less on internal funds. Employing the EURACE model, Raberto et al. (2012) find that lower capital-adequacy ratios can spur growth in the short-run, but the higher stock of private debt can lead to higher firm bankruptcies, credit rationing and more serious economic downturns in the long-run. The impact of capital and reserve requirements is studied in van der Hoog & Dawid (2015) with the Eurace@Unibi model (Dawid et al. 2012b). Simulation results show that stricter liquidity regulations are better suited to reduce output volatility and prevent deep downturns, whereas more stringent capital requirements obtain opposite results as they increases credit prociclicality (see also Van der Hoog 2015). Alternative resolution mechanisms of banking crises - i.e. liquidation of distressed institution, bank bail-out or bail-in - are studied in Klimek et al. (2015). They find that during expansions, closing the distressed bank is the best policy to achieve financial and economic stability, whereas bail in is the desired one during recessions. Finally, the impact of Basel II regulation on financial market dynamics is studied in Poledna et al. (2014) with an ABM populated by fund managers and representative noisy trader, bank, and fund investor (see also Aymanns & Farmer 2015). The simulation of the ABM shows that Basel II has a destabilizing impact on the market by increasing the amount of synchronized buying and selling needed to achieve deleveraging. As a consequence, Basel II reduces default risk when leverage is low, but it magnifies it when leverage is high
A new generation of agent-based models has been recently employed to study the effects of the introduction of Basel III macroprudential regulation and its possible interactions with monetary policy to achieve both price and financial stability28. Popoyan et al. (2015) extend the ABM developed in Ashraf et al. (2011) to address such issues exploring the joint and stand-alone impact of the different levers of Basel III for alternative monetary policies e.g. conservative, dual-mandate Taylor rule, or "leaning against the wind" monetary rule focused on inflation, output gap and credit growth. Simulation results show that a triple- mandate Taylor rule and the full-fledge Basel III prudential regulation is the best policy mix to improve the stability of the banking sector and smooth output fluctuations. However, results close to the Basel III first-best can be achieved in a much more simplified regulatory framework by adopting just minimum capital requirements and counter-cyclical capital buyers (see also Cincotti et al. 2012a, for similar conclusions concerning the stabilizing role of counter-cyclical capital buyers). Moreover, the components of Basel III are non-additive: the inclusion of an additional lever does not always improve the performance of the macroprudential regulation and their joint impact is more effective than the sum of their individual contributions. In line with the previous results, also Krug et al. (2015) find that Basel III improves the resilience of the banking system and the effects of microprudential instruments are non-additive. Moreover, surcharges on systemic important banks increase financial regulation complexity without increasing the stability of the banking sector. A strong complementarity between macroprudential and monetary policy is also found in Krug (2015): in line with the Tinbergen principle, a "leaning against the wind" monetary rule is not sufficient alone to prevent financial instability. The ABM developed by Da Silva & Tadeu Lima (2015) provide somewhat different results: countercyclical capital buyer can lose its efficacy in stabilizing the financial system when combined with some monetary rules, and interest rate smoothing is the most successful monetary policy strategy.
The modeling of the network structure of an economy is difficult in DSGE models. This lack of consideration has prevented such models to explain the emergence, the depth and the diffusion of the current crisis, where the topological properties of the credit market network have a fundamental. Taking a complexity theory perspective and combining network theory and agent-based model can improve financial regulation and providing early signals, which could help to avoid the occurrence of financial crises (Battiston et al. 2016). For instance, Battiston et al. (2012) show that the financial network is more resilient for intermediate levels of risk diversification than for the highest one. The resilience of the banking network to liquidity shocks is studied by Gai et al. (2011) developing an agent-based model of the interbank lending network where heterogeneous banks are randomly connected together though unsecured claims and repo activities. The impact of idiosyncratic liquidity shocks are then analyzed for different network configurations, degrees of connectivity between banks, haircut assumptions, and balance sheet characteristics of financial institutions. The model shows that greater degree of complexity and concentration in the bank network augment the fragility of system, increasing the probability of contagion phenomena and liquidity crises similar to the ones experienced in the Great Recession. Policy experiments show possible ways (e.g. tougher micro-prudential liquidity regulation, countercyclical liquidity requirements) to reduce the network externalities responsible for the emergence of systemic crisis. The effects of solvency shocks are considered in Krause & Giansante (2012), who find that the topological properties of the interbank lending network affect the diffusion of crises originated by the failure of a failing bank. Gaffeo & Molinari (2016) study the resilience of the banking network as to a sequence of merging and acquisitions episodes which affect its topology. They find that the consolidation of the banking network has different impact on systemic risk according to the size of interbank market and bank capitalization. As a consequence, policy makers should monitor the time evolution of the interbank network before authorizing bank consolidation29.
An increasing number of ABM analyze the connections between bank and firm networks and macroeconomic performance. Gabbi et al. (2015) add a stylized real sector to an ABM of the banking network and study the impact of some macroprudential regulations (e.g. countercyclical capital buyers). They find that the impact of the regulatory framework on banks performance vary in a complex way with the state of the economy, the degree of connectivity of the interbank network and the amount of available information on bank risks. The emergence of a network-based financial accelerator is analyzed in Delli Gatti et al. (2010), who develop an ABM populated by heterogeneous banks, financially constrained downstream and upstream firms interacting on a continuously evolving credit network. Simulation results show that the emergence and evolution of the network-based financial accelerator lead to financial crises and business cycles. Hence, policy makers can try to design a structure for the credit network in order to reduce the magnifying effects of the financial accelerator (e.g. Grilli et al. 2014 find that macroeconomic performance increases with network connectivity up to a certain threshold). In particular, in an extended version of the model, Riccetti et al. (2013a) find that leverage has a destabilizing effect, increasing the risk in the economy and dampening the effects of monetary policy (relatedly, Lengnick et al. 2013 find that interbank market stabilizes the economy during normal times but it acts as destabilizer during crises). Moreover, if the banking system is not sufficiently capitalized, a surge in Central Bank interest rate may increase its fragility, whereas an increase of the reserve coefficient improves the resilience of bank network to shocks. Starting from the previous works, Catullo et al. (2015) develop an early warning indicator for crises grounded on the evolution of the firm-bank credit network.
The housing market has a source of financial instability and contagion possibly leading to crises has started to be addressed by agent-based models. Geanakoplos et al. (2012) build an ABM of the housing market for the greater Washington DC area. The model matches the house price and housing market indices from 1997-2010 and it suggests that the housing boom and bust has been mainly driven by leverage rather than interest rates. Gangel et al. 2013) study the contagion effects of foreclosure in a real-estate market and find that the time a foreclosed property stay in the market has a much stronger effect on market stability than any contagion effect. Such results suggest that policy makers should simplify and speed up the process of dissolving foreclosed houses.
Labor market policy
In DSGE models, labor market is not usually modeled and unemployment is not contemplated (see Section 3 above). This prevents them to study problems related to involuntary unemployment, structural reforms, human capital policies, etc.
The K+S model is extend in Dosi et al. (2016e, 2016d) to account for different microfounded labor-market regimes characterized by different levels of wage flexibilities, labor mobility and institutions (e.g. minimum wage, unemployment benefits). The model generates persistent involuntary unemployment and it accounts for several stylized facts of the labor market (e.g. wage, Beveridge and Okun curves, productivity, unemployment and vacancy rates volatility, etc.). Simulation results also show that more rigid labor markets and labour relations lead to higher productivity and GDP growth, as well as to lower inequality, unemployment and output volatility. In line with the intuitions of Stiglitz (2011, 2015), the negative effects of wage flexibility on macroeconomic dynamics are found also in Napoletano et al. (2012) and Seppecher (2012), while Riccetti et al. (2013b) find that unemployment benefits stabilize output fluctuations.
In a series of papers, Dawid et al. (2012a, 2014a, 2014b) employ the Eurace@Unibi model to analyze the convergence of regions characterized by local labor markets where workers have heterogeneous skills. In particular, they study the impact of policies aimed at improving workers skills and firms’ technological adoption on innovation, commuting flows, inequality dynamics and economic convergence. Simulation results show that both policies are complementary and that human capital policies foster regional cohesion only if labor markets are separated (Dawid et al. 2014b). Moreover, the effects of policies depends on the flexibility of the labor markets (Dawid et al. 2014a).
Climate policy
General equilibrium models are not well suited to analyze the effects of climate policies as their strong (hyper-rational representative agent) and often ad-hoc assumptions (Pindyck 2013) conflict with the strong non-linearities, tipping points and irreversible dynamics associated to climate change. On the contrary, agent-based models can naturally account for out-of equilibrium dynamics in framework characterized by strong uncertainties. Not surprisingly, a new generation of agent-based models studying the intricate links between economic growth and climate at regional, national, and global level have blossomed in the last years (see Balint et al. 2016, for a detailed survey).
The interactions between complex economic dynamics and climate change are explored in the LAGOM model family (Mandel et al. 2010; Wolf et al. 2013b), where economic growth is endogenously generated by a spatially explicit production network. As in each region carbon emissions are a by-product of energy production, the model can be employed to assess the effect of different mitigation policies. Gerst et al. (2013) expand the K+S model (Dosi et al. 2010) to account for energy inputs as well as for a simplified energy system. They employ the model to compare a business-as-usual framework vis-à-vis policy scenarios where a carbon tax is introduced and its revenues are employed to provide rebates to households, to support industrial R&D, or to invest in car-bon free R&D. The model is calibrated on U.S. data and simulated until the end of the XXI century. They find that all the policy schemes reduce greenhouse gasses emissions, but only the carbon-free R&D policy allows a swift transition away from "dirty" energy technologies, and, in turns, to higher economic growth. The latter policy scheme allows to minimize carbon emissions also in the ABM developed by Rengs et al. (2015). However, the best performance in terms of unemployment is achieved when the Government levies taxes on carbon emissions rather than on labor. Starting from an ABM of technology diffusion, Robalino & Lempert (2000) find that a combined strategy of carbon taxes and technology subsidies is the best policy to reduce greenhouse gas emissions.
Building on the K+S model, Isley et al. (2013) explore how firms can both innovate to reduce their carbon intensity and lobby the government for altering carbon taxes. Simulation results show that carbon-reducing technological opportunities have a strong impact on the decarbonization rate of the economy as well as on the carbon price lobby. Different types of green fiscal (carbon tax, tax relief and breaks on investment in renew-able energy) and targeted monetary policies (green bonds and quantitative easing) are simulated in the Eirin model (Monasterolo & Raberto 2016), which combine a system dynamics and agent-based features. They find that green policy measures allow to improve economic performance, and reduce financial instability vis-à-vis a business-as-usual scenario. Finally, Lamperti et al. (2016a) expand the K+S model to provide a detailed representation of climate-economic non-linear feedbacks in order to test the short- and long-run effects of different ensemble of innovation, fiscal and monetary policies in scenarios where climate disasters can considerably harm the economic dynamics.
Concluding Remarks
The Great Recession has prompted a debate about the state of macroeconomic theory. Certainly, we stand in the camp of those arguing that macroeconomics has entered in a Dark Age (Krugman 2011), where dismissing facts that do not conform to "post-real" models is the norm (Romer 2016)30. Indeed, as discussed in Section 3, DSGE models suffer from a series of dramatic problems and difficulties concerning their inner logic consistency, the way they are taken to the data, the extent to which they are able to replicate existing reality, and the realism of their assumptions. These problems are so deep that prevent DSGE models even to conceive the possibility of the current crisis and propose viable solutions to policymakers. The acknowledgement of such limitations has stimulated new research, which has led to the introduction in DSGE models of financial frictions, mild form of agent heterogeneity and bounded rationality, as well as fat-tailed exogenous shocks. We think that these new developments are welcome but they only patch clothes that are not possible to mend. Indeed, the intrinsic difficulties of DSGE models are so hard to solve within the straight jacket of the neoclassical paradigm (rationality, equilibrium, etc.) that a different research avenue, grounded on complexity science is more fruitful.
This alternative paradigm does actually exist and it is called agent-based computational economics (ACE). Section 5 has been devoted to a (necessarily) brief discussion of its philosophical underpinnings, building blocks and policy applications. As our survey shows (cf. Section 6), the number of areas where ACE policy experiments have been already applied with success is rather vast and rapidly increasing, especially after the policy challenges posed by the Great Recession. To have a better feel of this, it suffices to compare the number and breadth of the agent-based model (ABM) applications surveyed in Fagiolo & Roventini (2012) with those covered here. The discussion of Section 5 has also outlined the most prominent values added deriving from performing policy experiments within an ACE approach. These include behavioral assumptions grounded on empirical and experimental evidence; ACE’s extreme modeling flexibility; the friendly relation of agent-based models with empirical data; the easiness of carrying out empirical-validation exercises; the almost infinite possibility of experimentation; and, last but not least, the positive impact that a more realistic and algorithmically-structured model can have on political decision makers – as compared to obscure and unintuitive mathematical neoclassical models.
Of course, as happens for the New Neoclassical Synthesis, many issues are still far from being settled and the debate is very open. Here, by a way of conclusion, we recall some of them.
The first issue – which we can label as the problem of over-parametrization – has to do with the role played by micro and macro parameters in ABMs. As mentioned, ABMs are often over-parameterized, for one typically injects in the specification of agents’ behavioral rules and interaction patterns many ingredients in order to meet as much as possible what he/she observes in reality. Suppose for simplicity that initial conditions do not matter. Even if empirical validation can provide a way to reduce free parameters, the researchers are almost always left with an ABM whose behavior depends on many free parameters. Many questions naturally arise. How can one interpret these different parameterizations? Which one should be used if one employs the model to deliver policy implications? Should one perfectly calibrate (if possible) the model using the data so that no free parameters are left? Should policy implications be robust to alternative parameterizations instead? Notice that this issue is closely related to a common critique that ABMs usually face: if an ABM contains many free parameters and it is able to reproduce a given set of stylized facts, how can one be sure that it represents the minimal mechanisms capable of reproducing the same set of stylized facts? This point reminds the "unconditional objects" critique in Brock (1999) and it is certainly true for "oversized" ABMs. Despite such an issue is still not completely settled, much progresses has been made in the last years on this side, as our discussion on estimation and calibration of agent-based model parameters indicate (cf. Section 5).
The second issue concerns the role played by initial conditions. Recall that (if random ingredients are present in the model) any ABM can be considered as an artificial (stochastic) data generation process (mDGP) with which we try to approximate the one that generated the data that we observe (i.e., the rwDGP). The question is as follows: Is the rwDGP ergodic or not? If the underlying real-world rwDGP is thought to be non-ergodic (as well as the theoretical mDGP described in the AB model), then initial conditions matter. This raises a whole host of problems for the modeler. The modeler needs to identify the "true" set of initial conditions in the empirical data, generated by the rwDGP, in order to correctly set the initial parameters of the model. Even if the "perfect database" would exist, this is a very difficult task. How far in the past, does one need to go in order to identify the correct set of initial values for the relevant micro and macro variables? There is a possibility of infinite regress. If this is the case, then one may need data stretching back a very long time, possibly before data collection. Again, as compared to the situation discussed in Fagiolo & Roventini (2012), there has been some progress also in this respect, especially in the efforts devoted to identifying ergodicity tests for ABMs (see Section 5).
This issue is closely related to a third one, regarding the relation between simulated and real-world data. While in principle we could generate as many theoretical observations as we like, in practice we may only have a few of such empirical realizations (possibly only one!). If we believe that the empirical observations come from an underlying DGP that could have been "played twice" (i.e., could have generated alternative observations, other than the one we have) the problem of comparing simulated with empirical data becomes very complicated.
All the three issues above affect any stochastic, dynamic (economic) model, DSGE-based ones included. Indeed, they are the subject of never-ending debates among philosophers of science, since they raise fundamental questions related to probability, modeling, inference, etc. (see, e.g., Fagiolo et al. 2007b). Nevertheless, the large majority of those advocating the New Neoclassical Synthesis approach seems not to care about them. In our view, the fact that they instead occupy center stage in the current ACE debate is another signal of the vitality of this young but promising paradigm.
The last issue worth mentioning is specific to ACE and it concerns the comparability of different agent-based models. DSGE models are all built using a commonly-shared set of behavioral rules (e.g., representative agents solving a stochastic dynamic optimization problems) and their empirical performance is assessed with com-mon techniques (i.e., VAR models). This allows to develop a common protocol about "how to do macroeconomics with DSGE models" and it eases the comparison of the results produced by competing models. Given the relatively infancy of the ACE paradigm, the lack of such a widespread agreement among the ACE community hinders the dialogue among different ABMs, reducing the comparability of their results, and possibly slowing down new developments. In that respect, the development of common documentation guidelines (Wolf et al. 2013a), dedicated languages and platforms31 can surely improve the situation, increase the exchanges among ACE scholars, and reduce the entry cost to agent-based modeling.
Acknowledgements
Thanks to Mattia Guerini, Francesco Lamperti, Manuel Scholz-Wäckerle, and Tania Treibich. All usual disclaimers apply. This paper has been supported by two European Union’s Horizon 2020 grants: No. 649186 - Project ISI-Growth and No. 640772 - Project Dolfins.Notes
- For a detailed presentation of different schools of thought in modern macroeconomics see Snowdon & Vane (2005).
- For an introduction, see Clarida et al. (1999), Woodford (2003) and Galí & Gertler (2007). Cf. also Colander (2006c) for an historical perspective.
- At the opposite, according to Howitt (2011) "macroeconomic theory has fallen behind the practice of central banking" (p. 2). On the same camp, Mankiw (2006) thinks that macroeconomists should not behave as scientist but as engineers trying to solve practical problems. See also Summers (1991) for an extremely pessimistic view on the possibility of taking any economic model seriously econometrically. On these points see also Mehrling (2006).
- More precisely, in Section 3 we argue that the DSGE policy apparatus is plagued by a long list of serious problems concerning theoretical issues (i.e., having to do with formal inconsistencies of the model – given its assumptions), empirical difficulties (i.e., related to empirical validation of DSGE models) and political-economy issues (i.e., concerning the absence of any justification for the often unrealistic and over-simplifying assumptions used two derive policy implications). See also Colander (2006b).
- Robert Solow commented that although the NKP curve might be new, it is neither Keynesian, nor a Phillips curve. Indeed, the NKP curve implies that (i) inflation jumps instantaneously whenever there is a variation in the output gap, (ii) positive output gaps lead to fall in the inflation rate; (iii) disinflation is not costly (see Carlin & Soskice 2014, for a detailed discussion).
- A discussion of the limits of the representative assumption in light of the current crisis is contained in Kirman (2010).
- Of course, also other monetary policy rules different from the Taylor rule (cf. eq. 3) can lead to a local determinate rational-expectation equilibrium.
- On this and related points addressing the statistical vs. substantive adequacy of DSGE models, see Poudyal & Spanos (2013).
- See also Beyer & Farmer (2004) and the discussion in Romer (2016).
- Fukac & Pagan (2006) also argue that identification problems are usually partly mitigated by arbitrarily assuming serially correlated shocks.
- An exception is Curdia et al. (2014) where shocks are drawn from a Student-t distribution. More on that in Section 4.
- On the contrary, the LSE-Copenhagen school follows a macroeconometric modeling philosophy orthogonal to the one followed by DSGE modelers. Scholars of the LSE-Copenhagen approach have concentrated their e orts on improving the statistical model in order to structure data with an identified co-integrated VAR that could then be used to produce stylized facts for theoretical models (Johansen & Juselius 2006; Juselius & Franchi 2007).
- This is what mainstream macroeconomics consider "sound microfoundations". However, as Kirman (2016) put it: "the rationality attributed to individuals is based on the introspection of economists rather than on careful empirical observation of how individuals actually behave".
- As Kirman (2016) put it, Muth (1961) was very aware that rational expectation is a convenient short cut, but little evidence suggests that it provides a satisfactory explanation of economic reality.
- Moreover, since agents can swap IOUs without facing any credit risk, money has only the function of unit of account and it can be ruled out from DSGE models. Indeed, when money is present in the utility function of consumers, the transactions requiring money are assumed to be sufficiently unimportant, so for "reasonable" calibrations, money-augmented DSGE models deliver almost the same results of the standard ones (Woodford 2003, chapter 2).
- Large-scale DSGE models with financial frictions have been recently developed at IMF (Benes et al. 2014) and at the Federal Reserve (Del Negro et al. 2013).
- Lengnick & Wohltman (2016) develop a hybrid DSGE model where the financial market is represented by an agent-based model. See also Guerini et al. (2016) for an ABM which can be directly compared to a plain-vanilla DSGE model.
- Fagiolo et al. (2008) find that GDP growth rates distributions are well proxied by double exponential densities, which dominate both Student’s t and Levy-stable distributions. In light of such results, the choice of Curdia et al. (2014) to drawn shocks from a Student’s t distribution is not only ad-hoc, but not supported by the empirical evidence.
- Lindé et al. (2016) also conclude that more non-linearities and heterogeneity are required to satisfactory account of default risk, liquidity dynamics, bank runs, as well as to study the interactions between monetary and macroprudential policies.
- This and the following subsections heavily draw from Pyka & Fagiolo (2007) and Fagiolo et al. (2007b). For further details see, among others, Dosi & Egidi (1991), Dosi et al. (2005), Lane (1993), Tesfatsion & Judd (2006), Colander (2006a) and Tesfatsion (2006b).
- This has to be contrasted with the neoclassical approach, where agents hold rational expectations and, as Mehrling (2006, p. 76) puts it, "the future, or rather our ideas about the future, determines the present".
- For a more in-depth discussion of empirical validation in ABMs, we refer the reader to Fagiolo et al. (2007a), Pyka & Werker (2009) and papers therein.
- See the special issues edited by Fagiolo et al. (2007a) in Computational Economics and by Pyka & Werker (2009) in the Journal of Artificial Societies and Social Simulation, and the paper by Moss (2008).
- See for example the papers contained in the special issues on agent-based models and economic policies edited by Dawid & Fagiolo (2008) and Gaffard & Napoletano (2012).
- Moss (2008) discusses the importance of involving the actual decision makers in the process of the generation of agent-based models for policy evaluation.
- More generally, the model of Dosi et al. (2010) highlights a strong complementarity between Keynesian policies affecting demand and Schumpeterian policies affecting innovation.
- The impact of inequality on macroeconomic performance is also explored in Ciarli et al. (2012), Isaac (2014), Cardaci & Saraceno (2015), and Russo & Gallegati (2016).
- Alternative macroprudential and regulation policies are explored in van der Hoog (2015) employing the Eurace@Unibi model.
- See Galbiati & Soramaki (2011) for an agent-based model studying the efficiency of the interbank payment system under alternative system configurations.
- Romer (2016) also contains a deep discussion on why "post-real" macroeconomics has emerged and why the current norms in the economic profession make it difficult to jettison it.
- Among an increasing number of languages and platforms for ABM one can consider NetLogo (https://ccl.northwestern.edu/netlogo/), LSD (http://www.labsimdev.org/Joomla_1-3/), JAS-mine (http://www.jas-mine.net), and JMAB (https://github.com/S120/jmab/tree/master).
References
AKERLOF, G. A. (2002). Behavioral macroeconomics and macroeconomic behavior. American Economic Review, 92, 411–433. [doi:10.1257/00028280260136192]
AKERLOF, G. A. (2007). The missing motivation in macroeconomics. American Economic Review, 97, 5–36. [doi:10.1257/aer.97.1.5]
AKERLOF, G. A. & Shiller, R. J. (2009). Animal Spirits: How Human Psychology Drives the Economy, and Why It Matters for Global Capitalism. Princeton, NJ, Princeton University Press.
ALBERT, R. & Barabasi, A. L. (2002). Statistical mechanics of complex networks. Rev. Mod. Phys, 4, 47–97. [doi:10.1103/RevModPhys.74.47]
ALESSI, L., Barigozzi, M. & Capasso, M. (2007). A review of nonfundamentalness and identification in structural VAR models. Working Paper 2007/22, Laboratory of Economics and Management (LEM), Scuola Superiore Sant’Anna, Pisa, Italy.
ALFARANO, S., Lux, T. & Wagner, F. (2005). Estimation of agent-based models: The case of an asymmetric herding model. Computational Economics, 26, 19–49. [doi:10.1007/s10614-005-6415-1]
ANUFRIEV, M., Assenza, T., Hommes, C. & Massaro, D. (2013). Interest Rate Rules and Macroeconomic Stability Under Heterogeneous Expectations. Macroeconomic Dynamics, 17(08), 1574–1604. [doi:10.1017/S1365100512000223]
AOKI, M. (2006). ‘Not more so: Some concepts outside the DSGE framework’. In D. Colander (Ed.), Post Walrasian Macroeconomics. Cambridge, Cambridge University Press. [doi:10.1017/cbo9780511617751.010]
ARIFOVIC, J., Dawid, H., Deissenberg, C. & Kostyshyna, O. (2010). Learning benevolent leadership in a heterogeneous agents economy. Journal of Economic Dynamics & Control, 34(9), 1768–1790. [doi:10.1016/j.jedc.2010.06.023]
ARIFOVIC, J. & Maschek, M. K. (2012). Currency crisis: Evolution of beliefs and policy experiments. Journal of Economic Behavior & Organization, 82, 131–150. [doi:10.1016/j.jebo.2012.01.001]
ASCARI, G., Fagiolo, G. & Roventini, A. (2015). Fat-tails distributions and business-cycle models. Macroeconomic Dynamics, 19, 465–476. [doi:10.1017/S1365100513000473]
ASCARI, G. & Ropele, T. (2009). Trend inflation, Taylor principle, and indeterminacy. Journal of Money, Credit and Banking, 41, 1557–1584. [doi:10.1111/j.1538-4616.2009.00272.x]
ASHRAF, Q., Gershman, B. & Howitt, P. (2011). Banks, market organization, and macroeconomic performance: An agent-based computational analysis. Working Paper 17102, NBER. [doi:10.3386/w17102]
ATKINSON, A. B., Piketty, T. & Saez, E. (2011). Top incomes in the long run of history. Journal of Economic Literature, 49, 3–71. [doi:10.1257/jel.49.1.3]
AUERBACH, A. J. & Gorodnichenko, Y. (2012). ‘Fiscal multipliers in recession and expansion’. In Fiscal Policy after the Financial Crisis. National Bureau of Economic Research, Inc.
AYMANNS, C. & Farmer, D. J. (2015). The dynamics of the leverage cycle. Journal of Economic Dynamics & Control, 50, 155–179. [doi:10.1016/j.jedc.2014.09.015]
BALINT, T., Lamperti, F., Mandel, A., Napoletano, M., Roventini, A. & Sapio, S. (2016). Complexity and the economics of climate change: A survey and a look forward. Working paper series 2016/29, Laboratory of Economics and Management (LEM), Scuola Superiore Sant’Anna, Pisa, Italy.
BARDE, S. (2015). A practical, universal, information criterion over nth order Markov processes. Discussion Paper 15/04, University of Kent School of Economics.
BARGIGLI, L., Riccetti, L., Russo, A. & Gallegati, M. (2016). Network calibration and metamodeling of a financial accelerator agent based model. Working Papers - Economics 2016/01, Universita’ degli Studi di Firenze, Di-partimento di Scienze per l’Economia e l’Impresa. [doi:10.2139/ssrn.2712715]
BASSI, F. & Lang, D. (2016). Investment hysteresis and potential output: A post-Keynesian–Kaleckian agent-based approach. Economic Modelling, 52, 35–49. [doi:10.1016/j.econmod.2015.06.022]
BATTISTON, S., Delli Gatti, D., Gallegati, M., Greenwald, B. & Stiglitz, J. (2012). Liaisons dangereuses: Increasing connectivity, risk sharing, and systemic risk. Journal of Economic Dynamics & Control, 36, 1121–1141. [doi:10.1016/j.jedc.2012.04.001]
BATTISTON, S., Farmer, D. J., Flache, A., Garlaschelli, D., Haldane, A., Heesterbeeck, H., Hommes, C., Jaeger, C., May, R. & Scheffer, M. (2016). Complexity theory and financial regulation. Science, 351, 818–819. [doi:10.1126/science.aad0299]
BENES, J., Kumhof, M. & Laxton, D. (2014). Financial crises in DSGE models: A prototype model. IMF Working Paper 14/57, International Monetary Fund. [doi:10.5089/9781475540895.001]
BENHABIB, J., Schmitt-Grohé, S. & Uribe, M. (2001). The perils of Taylor rules. Journal of Economic Theory, 96, 40–69. [doi:10.1006/jeth.1999.2585]
BERNANKE, B., Gertler, M. & Gilchrist, S. (1999). ‘The financial accelerator in a quantitative business cycle framework’. In J. Taylor & M. Woodford (Eds.), Handbook of Macroeconomics. Elsevier Science: Amsterdam.
BEYER, A. & Farmer, R. E. A. (2004). On the indeterminacy of new-Keynesian economics. Working Paper Series No. 323, European Central Bank, Frankfurt, Germany.
BLANCHARD, O., Dell’Ariccia, M. G. & Mauro, M. P. (2013). Rethinking macro policy II: Getting granular granular. Tech. Rep. 13/03, IMF Staff Discussion Paper. [doi:10.5089/9781484363478.006]
BLANCHARD, O. & Galí, J. (2010). Labor markets and monetary policy: A new Keynesian model with unemployment. American Economic Journal: Macroeconomics, 2, 1–30. [doi:10.1257/mac.2.2.1]
BRANCH, W. A. & McGough, B. (2011). Monetary policy and heterogeneous agents. Economic Theory, 47, 365–393. [doi:10.1007/s00199-010-0539-9]
BROCK, W. A. (1999). Scaling in economics: A reader’s guide. Industrial and Corporate Change, 8, 409–46. [doi:10.1093/icc/8.3.409]
BROCK, W. A., Durlauf, S., Nason, J. M. & Rondina, G. (2007). Simple versus optimal rules as guides to policy. Journal of Monetary Economics, 54, 1372–1396. [doi:10.1016/j.jmoneco.2007.06.008]
BROCK, W. A. & Durlauf, S. N. (2001). ‘Interactions-based models’. In J. Heckman & E. Leamer (Eds.), Handbook of Econometrics, vol. 5. Amsterdam, North Holland. [doi:10.1016/s1573-4412(01)05007-3]
BROCK, W. A. & Hommes, C. (1997). A rational route to randomness. Econometrica, 65, 1059–1095. [doi:10.2307/2171879]
CABALLERO, R. J. (2010). Macroeconomics after the crisis: Time to deal with the pretense-of-knowledge syndrome. Journal of Economic Perspectives, 24, 85–102. [doi:10.1257/jep.24.4.85]
CAIANI, A., Godin, A., Caverzasi, E., Gallegati, M., Kinsella, S. & Stiglitz, J. (2015). Agent based-stock flow consistent macroeconomics: Towards a benchmark model. Research Paper 15-87, Columbia Business School. [doi:10.2139/ssrn.2664125]
CALVO, G. A. (1983). Staggered prices in a utility-maximizing framework. Journal of Monetary Economics, 12, 383–398. [doi:10.1016/0304-3932(83)90060-0]
CANOVA, F. (2008). How much structure in empirical models? In T. Mills & K. Patterson (Eds.), Palgrave Handbook of Econometrics, vol. 2, Applied Econometrics. Palgrave Macmillan.
CANOVA, F. & Sala, L. (2009). Back to square one: Identification issues in DSGE models. Journal of Monetary Economics, 56, 431–449. [doi:10.1016/j.jmoneco.2009.03.014]
CANZONERI, M., Collard, F., Dellas, H. & Diba, B. (2016). Fiscal multipliers in recessions. The Economic Journal, 126, 75–108. [doi:10.1111/ecoj.12304]
CARDACI, A. & Saraceno, F. (2015). Inequality, financialisation and economic crises: An agent-based macro model. Working paper 2015-27, OFCE.
CARLIN, W. & Soskice, D. (2014). Macroeconomics: Institutions, Instability, and the Financial System. Oxford, Oxford University Press.
CATULLO, E., Gallegati, M. & Palestrini, A. (2015). Towards a credit network based early warning indicator for crises. Journal of Economic Dynamics & Control, 50, 78–97. [doi:10.1016/j.jedc.2014.08.011]
CHARI, V. V., Kehoe, P. J. & R., M. E. (2009). New Keynesian models are not yet useful for policy analysis. American Economic Journal: Macroeconomics, 1, 242–266. [doi:10.1257/mac.1.1.242]
CHIARELLA, C. & Di Guilmi, C. (2012). The fiscal cost of financial instability. Studies in Nonlinear Dynamics & Econometrics, 16, 1–27. [doi:10.1515/1558-3708.1970]
CHRISTIANO, L. G., Eichenbaum, M. & Evans, C. L. (2005). Nominal rigidities and the dynamic effects of a shock to monetary policy. Journal of Political Economy, 113, 1–45. [doi:10.1086/426038]
CHRISTIANO, L. G., Motto, R. & Rostagno, M. (2011). Financial factors in economic fluctuations. Working Paper Series 1192, European Central Bank.
CHRISTIANO, L. G., Motto, R. & Rostagno, M. (2013). Risk shocks. American Economic Review, 104, 27–65. [doi:10.1257/aer.104.1.27]
CIARLI, T., Lorentz, A., Savona, M. & Valente, M. (2012). The role of technology, organisation, and demand in growth and income distribution. Working Paper Series 2012/06, Laboratory of Economics and Management (LEM), Scuola Superiore Sant’Anna, Pisa, Italy.
CINCOTTI, S., Raberto, M. & Teglio, A. (2010). Credit money and macroeconomic instability in the agent-based model and simulator EURACE. Economics: The Open-Access, Open-Assessment E-Journal, 4(2010-26).
CINCOTTI, S., Raberto, M. & Teglio, A. (2012a). Macroprudential policies in an agent-based artificial economy. Revue de l’OFCE, 124, 205–234. [doi:10.3917/reof.124.0205]
CINCOTTI, S., Teglio, A. & Raberto, M. (2012b). The EURACE macroeconomic model and simulator. In Agent-based Dynamics, Norms, and Corporate Governance. The proceedings of the 16-th World Congress of the International Economic Association. Palgrave.
CLARIDA, R., Galí, J. & Gertler, M. (1999). The science of monetary policy: A new Keynesian perspective. Journal of Economic Literature, 37, 1661–1707. [doi:10.1257/jel.37.4.1661]
COGAN, J. F., Cwik, T., Taylor, J. B. & Wieland, V. (2009). New Keynesian versus old Keynesian government spending multipliers. Journal of Economic Dynamics & Control, 34, 281–295. [doi:10.3386/w14782]
COGLEY, T. & Nason, J. M. (1993). Impulse dynamics and propagation mechanisms in a real business cycle model. Economic Letters, 43, 77–81. [doi:10.1016/0165-1765(93)90138-3]
COIBION, O. & Gorodnichenko, Y. (2011). Information rigidity and the expectations formation process: A simple framework and new facts. Working Paper Series 16537, NBER.
COLANDER, D. (2005). The future of economics: the appropriately educated in pursuit of the knowable. Cambridge Journal of Economics, 29, 927–941. [doi:10.1093/cje/bei078]
COLANDER, D. (2006a). Introduction. In D. Colander (Ed.), Post Walrasian Macroeconomics. Cambridge, Cam-bridge University Press. [doi:10.1017/CBO9780511617751.002]
COLANDER, D. (Ed.) (2006b). Post Walrasian Macroeconomics. Cambridge, Cambridge University Press.
COLANDER, D. (2006c). ‘Post Walrasian macroeconomics: Some historic links’. In D. Colander (Ed.), Post Walrasian Macroeconomics. Cambridge, Cambridge University Press. [doi:10.1017/CBO9780511617751.004]
COLANDER, D., Folmer, H., Haas, A., Goldberg, M. D., Juselius, K., Kirman, A. P., Lux, T. & Sloth, B. (2009). The financial crisis and the systemic failure of academic economics. Tech. rep., 98th Dahlem Workshop. [doi:10.2139/ssrn.1355882]
COOPER, R. W. & John, A. (1988). Coordinating coordination failures in Keynesian models. Quarterly Journal of Economics, 103, 441–463. [doi:10.2307/1885539]
CURDIA, V., Del Negro, M. & Greenwald, D. (2014). Rare shocks, great recessions. Journal of Applied Econometrics, 29, 1031–1052. [doi:10.1002/jae.2395]
CURDIA, V. & Woodford, M. (2010). Credit spreads and monetary policy. Journal of Money, Credit and Banking, 42, 3–35. [doi:10.1111/j.1538-4616.2010.00328.x]
CURDIA, V. & Woodford, M. (2011). The central-bank balance sheet as an instrument of monetary policy. Journal of Monetary Economics, 58, 54–79. [doi:10.1016/j.jmoneco.2010.09.011]
CURDIA, V. & Woodford, M. (2015). Credit frictions and optimal monetary policy. NBER Working paper 21820, National Bureau of Economic Research.
DA SILVA, M. A. & Tadeu Lima, G. (2015). Combining monetary policy and prudential regulation: An agent-based modeling approach. Working paper 394, Banco Central do Brasil.
DAWID, H. & Fagiolo, G. (Eds.) (2008). Special Issue on "Agent-Based Models for Economic Policy Design". In Journal of Economic Behavior and Organization. 67. [doi:10.1016/j.jebo.2007.06.009]
DAWID, H., Gemkow, S., Harting, P. & Neugart, M. (2012a). Labor market integration policies and the convergence of regions: the role of skills and technology diffusion. Journal of Evolutionary Economics, 22, 543–562. [doi:10.1007/s00191-011-0245-1]
DAWID, H., Gemkow, S., Harting, P., van der Hoog, S. & Neugart, M. (2012b). The Eurace@Unibi model: An agent-based macroeconomic model for economic policy analysis. Tech. Rep. 05-2012, Bielefeld Working Papers in Economics and Management.
DAWID, H., Harting, P. & Neugart, M. (2014a). Cohesion policy and inequality dynamics: Insights from a heterogeneous agents macroeconomic model. Working paper series 34, SFB 882.
DAWID, H., Harting, P. & Neugart, M. (2014b). Economic convergence: Policy implications from a heterogeneous agent model. Journal of Economic Dynamics & Control, 44, 54–80. [doi:10.1016/j.jedc.2014.04.004]
DE GRAUWE, P. (2012). Booms and busts in economic activity: A behavioral explanation. Journal of Economic Behavior & Organization, 83, 484–501. [doi:10.1016/j.jebo.2012.02.013]
DEAK, S., Levine, P. & Yang, B. (2015). A new Keynesian behavioural model with individual rationality and heterogeneous agents. Working paper, University of Surrey.
DEBREU, G. (1974). Excess demand function. Journal of Mathematical Economics, 1, 15–23. [doi:10.1016/0304-4068(74)90032-9]
DEICHSEL, S. & Pyka, A. (2009). A pragmatic reading of Friedman’s methodological essay and what it tells us for the discussion on ABMS. Journal of Artificial Societies and Social Simulation, 12(4) 6: https://www.jasss.org/12/4/6.html.
DEL NEGRO, M., Eusepi, M., Giannoni, M. P., Sbordone, A., Tambalotti, A., Cocci, M., Hasegawa, R. & Linder, M. H. (2013). The FRBNY DSGE model. Tech. Rep. 647, Federal Reserve Bank of New York Staff Reports.
DELLI GATTI, D. & Desiderio, S. (2015). Monetary policy experiments in an agent-based model with financial frictions. Journal of Economic Interaction and Coordination, 10(2), 265-286. [doi:10.1007/s11403-014-0123-7]
DELLI GATTI, D., Di Guilmi, C., Gaffeo, E., Giulioni, G., Gallegati, M. & Palestrini, A. (2005a). A new approach to business fluctuations: Heterogeneous interacting agents, scaling laws and financial fragility. Journal of Economic Behavior & Organization, 56, 489–512. [doi:10.1016/j.jebo.2003.10.012]
DELLI GATTI, D., Gaffeo, E., Gallegati, M. & Palestrini, A. (2005b). The apprentice wizard: Monetary policy, complexity and learning. New Mathematics and Natural Computation, 1, 109–128. [doi:10.1142/S1793005705000068]
DELLI GATTI, D., Gallegati, M., Greenwald, B., Russo, A. & Stiglitz, J. (2010). The financial accelerator in an evolving credit network. Journal of Economic Dynamics & Control, 34, 1627–1650. [doi:10.1016/j.jedc.2010.06.019]
DELONG, J. B. (2011). Economics in crisis. The Economists’ Voice, May. [doi:10.2202/1553-3832.1854]
DILAVER, O., Jump, R. & Levine, P. (2016). Agent-based macroeconomics and dynamic stochastic general equilibrium models: Where do we go from here? Discussion Papers in Economics 01/16, University of Surrey.
DIXIT, A. & Stiglitz, J. (1977). Monopolistic competition and optimum product diversity. American Economic Review, 67, 297–308.
DOSI, G. (2012). Economic Organization, Industrial Dynamics and Development, chap. Introduction. Edward Elgar: Cheltenham.
DOSI, G. & Egidi, M. (1991). Substantive and procedural uncertainty: An exploration of economic behaviours in changing environments. Journal of Evolutionary Economics, 1, 145–68. [doi:10.1007/BF01224917]
DOSI, G., Fagiolo, G., Napoletano, M. & Roventini, A. (2013). Income distribution, credit and fiscal policies in an agent-based Keynesian model. Journal of Economic Dynamics & Control, 37, 1598–1625. [doi:10.1016/j.jedc.2012.11.008]
DOSI, G., Fagiolo, G., Napoletano, M., Roventini, A. & Treibich, T. (2015). Fiscal and monetary policies in complex evolving economies. Journal of Economic Dynamics & Control, 52(2014/22), 166–189. [doi:10.1016/j.jedc.2014.11.014]
DOSI, G., Fagiolo, G. & Roventini, A. (2010). Schumpeter meeting Keynes: A policy-friendly model of endogenous growth and business cycles. Journal of Economic Dynamics & Control, 34, 1748–1767. [doi:10.1016/j.jedc.2010.06.018]
DOSI, G., Marengo, L. & Fagiolo, G. (2005). ‘Learning in evolutionary environment’. In K. Dopfer (Ed.), Evolutionary Principles of Economics. Cambridge, Cambridge University Press. [doi:10.1017/cbo9780511492297.009]
DOSI, G., Napoletano, M., Roventini, A., Stiglitz, J. & Treibich, T. (2016a). Expectation formation, fiscal policies and macroeconomic performance when agents are heterogeneous and the world is changing. Working Paper Series forthcoming, Laboratory of Economics and Management (LEM), Scuola Superiore Sant’Anna, Pisa, Italy.
DOSI, G., Napoletano, M., Roventini, A. & Treibich, T. (2016b). Micro and macro policies in Keynes+Schumpeter evolutionary models. Journal of Evolutionary Economics. [doi:10.1007/s00191-016-0466-4]
DOSI, G., Napoletano, M., Roventini, A. & Treibich, T. (2016c). ‘The short- and long-run damages of fiscal austerity: Keynes beyond Schumpeter’. In J. Stiglitz & M. Guzman (Eds.), Contemporary Issues in Macroeconomics. Palgrave Macmillan UK. [doi:10.1057/9781137529589_9]
DOSI, G. & Nelson, R. R. (1994). An introduction to evolutionary theories in economics. Journal of Evolutionary Economics, 4, 153–72. [doi:10.1007/BF01236366]
DOSI, G., Pereira, M., Roventini, A. & Virgilito, M. E. (2016d). The effects of labour market reforms upon unemployment and income inequalities: an agent based model. Working Paper Series 2016/27, Laboratory of Economics and Management (LEM), Scuola Superiore Sant’Anna, Pisa, Italy.
DOSI, G., Pereira, M., Roventini, A. & Virgilito, M. E. (2016e). When more flexibility yields more fragility: the micro-foundations of Keynesian aggregate unemployment. Working Paper Series 2016/06, Laboratory of Economics and Management (LEM), Scuola Superiore Sant’Anna, Pisa, Italy.
DOSI, G., Pereira, M. & Virgillito, M. E. (2016f). On the robustness of the fat-tailed distribution of firm growth rates: A global sensitivity analysis. Working Paper Series 2016/12, Laboratory of Economics and Management (LEM), Scuola Superiore Sant’Anna, Pisa, Italy.
EGGERTSSON, G. B. & Krugman, P. (2012). Debt, deleveraging, and the liquidity trap: A Fisher-Minsky-Koo approach. Quarterly Journal of Economics, 127, 1469–1513. [doi:10.1093/qje/qjs023]
EVANS, G. W. & Honkapohja, S. (2001). Learning and Expectations in Macroeconomics. Princeton University Press. [doi:10.1515/9781400824267]
FABRETTI, A. (2012). On the problem of calibrating an agent based model for financial markets. Journal of Economic Interaction and Coordination, 8(2), 277–293. [doi:10.1007/s11403-012-0096-3]
FAGIOLO, G., Birchenhall, C. & Windrum, P. (Eds.) (2007a). Special Issue on "Empirical Validation in Agent-Based Models". In Computational Economics. Volume No. 30, Issue No. 3.
FAGIOLO, G., Moneta, A. & Windrum, P. (2007b). A critical guide to empirical validation of agent-based models in economics: Methodologies, procedures, and open problems. Computational Economics, 30, 195–226. [doi:10.1007/s10614-007-9104-4]
FAGIOLO, G., Napoletano, M. & Roventini, A. (2008). Are output growth-rate distributions fat-tailed? Some evidence from OECD countries. Journal of Applied Econometrics, 23, 639–669. [doi:10.1002/jae.1003]
FAGIOLO, G. & Roventini, A. (2012). Macroeconomic policy in DSGE and agent-based models. Revue de l’OFCE, 124, 67–116. [doi:10.3917/reof.124.0067]
FARMER, D. J. & Foley, D. (2009). The economy needs agent-based modeling. Nature, 460, 685–686. [doi:10.1038/460685a]
FAVERO, C. (2007). Model evaluation in macroeconometrics: From early empirical macroeconomic models to DSGE models. Working Paper 327, IGIER, Bocconi University, Milan, Italy.
FERNANDEZ-VILLAVERDE, J. & Levintal, O. (2016). Solution methods for models with rare disasters. Working Paper 21997, National Bureau of Economic Research. [doi:10.3386/w21997]
FERNANDEZ-VILLAVERDE, J., Rubio-Ramirez, J. F. & Sargent, T. J. (2005). A, b, c’s, (and d’s) for understanding VARs. Technical Working Paper 308, NBER. [doi:10.2139/ssrn.717963]
FERNANDEZ-VILLAVERDE, J., Rubio-Ramirez, J. F. & Schorfheide, F. (2016). Solution and estimation methods for DSGE models. Working Paper 21862, NBER. [doi:10.3386/w21862]
FERRARESI, T., Roventini, A. & Fagiolo, G. (2014). Fiscal policies and credit regimes: A TVAR approach. Journal of Applied Econometrics. 30(7), 1047-1072. [doi:10.1002/jae.2420]
FITOUSSI, J. & Saraceno, F. (2010). Inequality and macroeconomic performance. Document de Travail 2010-13, OFCE, Science Po.
FORNI, M. & Lippi, M. (1997). Aggregation and the Microfoundations of Dynamic Macroeconomics. Oxford, Oxford University Press.
FORNI, M. & Lippi, M. (1999). Aggregation of linear dynamic microeconomic models. Journal of Mathematical Economics, 31, 131–158. [doi:10.1016/S0304-4068(98)00060-3]
FRIEDMAN, M. (1953). ‘The methodology of positive economics’. In M. Friedman (Ed.), Essays in Positive Economics. Chicago, University of Chicago Press.
FUKAC, M. & Pagan, A. (2006). Issues in adopting DSGE models for use in the policy process. Working Paper 10/2006, CAMA.
FUKUYAMA, F. (1992). The End of History and the Last Man. London, Penguin.
GABBI, G., Iori, G., Jafarey, S. & Porter, J. (2015). Financial regulations and bank credit to the real economy. Journal of Economic Dynamics & Control, 50, 117–143. [doi:10.1016/j.jedc.2014.07.002]
GAFFARD, J.-L. & Napoletano, M. (Eds.) (2012). Agent-Based Models and Economic Policy. Revue de l’OFCE, 124.
GAFFEO, E. & Molinari, M. (2016). Macroprudential consolidation policy in interbank networks. Journal of Evolutionary Economics, 26, 77–99. [doi:10.1007/s00191-015-0419-3]
GAI, P., Haldane, A. & Kapadia, S. (2011). Complexity, concentration and contagion. Journal of Monetary Economics, 58, 453–470. [doi:10.1016/j.jmoneco.2011.05.005]
GALBIATI, M. & Soramaki, K. (2011). An agent-based model of payment systems. Journal of Economic Dynamics & Control, 35, 859–875. [doi:10.1016/j.jedc.2010.11.001]
GALÍ, J. (2008). Monetary Policy, Inflation, and the Business Cycle: An Introduction to the New Keynesian Framework. Princeton, NJ, Princeton University Press.
GALÍ, J. & Gertler, M. (2007). Macroeconomic modelling for monetary policy evaluation. Journal of Economic Perspectives, 21, 25–46. [doi:10.1257/jep.21.4.25]
GANGEL, M., Seiler, M. J. & Collins, A. (2013). Exploring the foreclosure contagion effect using agent-based modeling. Journal Real Estate Finance and Economics, 46, 339–354. [doi:10.1007/s11146-011-9324-1]
GEANAKOPLOS, J., Axtell, R., Farmer, D. J., Howitt, P., Conlee, B., Goldstein, J., Hendrey, M., Palmer, M. & Yang, C.-Y. (2012). Getting at systemic risk via an agent-based model of the housing market. American Economic Review, 102, 53–58. [doi:10.1257/aer.102.3.53]
GENNAIOLI, N., Ma, Y. & Shleifer, A. (2015). Expectations and investment. NBER Working paper 21260, National Bureau of Economic Research. [doi:10.3386/w21260]
GERST, M. D., Wang, P., Roventini, A., Fagiolo, G., Dosi, G., B., H. R. & Borsuk, M. E. (2013). Agent-based modeling of climate policy: An introduction to the engage multi-level model framework. Environmental Modelling & Software, 44, 62–75. [doi:10.1016/j.envsoft.2012.09.002]
GERTLER, M. & Karadi, P. (2011). A model of unconventional monetary policy. Journal of Monetary Economics, 58, 17–34. [doi:10.1016/j.jmoneco.2010.10.004]
GERTLER, M. & Kiyotaki, N. (2010). ‘Financial intermediation and credit policy in business cycle analysis’. In B. M. Friedman & M. Woodford (Eds.), Handbook of Monetary Economics. North Holland, Amsterdam. [doi:10.1016/b978-0-444-53238-1.00011-9]
GIGERENZER, G. (2007). Gut Feelings. The Intelligence of the Unconscious. New York: Viking.
GIGERENZER, G. & Brighton, H. (2009). Homo heuristicus: Why biased minds make better inferences. Topics in Cognitive Science, 1, 107–143. [doi:10.1111/j.1756-8765.2008.01006.x]
GILLI, M. & Winker, P. (2003). A global optimization heuristic for estimating agent based models. Computational Statistics & Data Analysis, 42(3), 299–312. [doi:10.1016/S0167-9473(02)00214-1]
GOODFRIEND, M. (2007). How the world achieved consensus on monetary policy. Journal of Economic Perspectives, 21, 47–68. [doi:10.1257/jep.21.4.47]
GOODFRIEND, M. & King, R. (1997). The new neoclassical synthesis and the role of monetary policy. NBER Macroeconomics Annual, (pp. 231–282). [doi:10.1086/654336]
GOODHART, C. A. E. (2009). The continuing muddles of monetary theory: A steadfast refusal to face facts. Economica, (76), 821–830. [doi:10.1111/j.1468-0335.2009.00790.x]
GRAZZINI, J. (2012). Analysis of the emergent properties: Stationarity and ergodicity. Journal of Artificial Societies and Social Simulation, 15(2) 7: https://www.jasss.org/15/2/7.html. [doi:10.18564/jasss.1929]
GRAZZINI, J. & Richiardi, M. (2015). Estimation of ergodic agent-based models by simulated minimum distance. Journal of Economic Dynamics & Control, 51(C), 148–165. [doi:10.1016/j.jedc.2014.10.006]
GRAZZINI, J., Richiardi, M. & Sellad, L. (2013). Indirect estimation of agent-based models. An application to a simple diffusion model. Complexity Economics, 2, 25–40. [doi:10.7564/13-COEC9]
GRAZZINI, J., Richiardi, M. & Tsionas, M. (2015). Bayesian estimation of agent-based models. Working Paper Series 145, LABORatorio R. Revelli, Centre for Employment Studies.
GREENWALD, B. & Stiglitz, J. (1993). New and old Keynesians. Journal of Economic Perspectives, 7, 23–44. [doi:10.1257/jep.7.1.23]
GREENWALD, B., Stiglitz, J., Hall, R. & Fischer, S. (1988). Examining alternative macroeconomic theories. Brookings Papers on Economic Activity, 1988, 207–270. [doi:10.2307/2534427]
GRILLI, R., Tedeschi, G. & Gallegati, M. (2014). Bank interlinkages and macroeconomic stability. International Review of Economics and Finance, 34, 72–88. [doi:10.1016/j.iref.2014.07.002]
GUALDI, S., Tarzia, M., Zamponi, F. & Bouchaud, J. (2015). Tipping points in macroeconomic agent-based models. Journal of Economic Dynamics & Control, 50, 29–61. [doi:10.1016/j.jedc.2014.08.003]
GUERINI, M. & Moneta, A. (2016). A method for agent-based models validation. Working Paper Series 2016/16, Laboratory of Economics and Management (LEM), Scuola Superiore Sant’Anna, Pisa, Italy.
GUERINI, M., Napoletano, M. & Roventini, A. (2016). No man is an island: The impact of heterogeneity and local interactions on macroeconomic dynamics. Working paper series 2016/24, Laboratory of Economics and Management (LEM), Scuola Superiore Sant’Anna, Pisa, Italy.
GUZMAN, G. (2009). ‘Using sentiment surveys to predict GDP growth and stock returns’. In L. R. Klein (Ed.), The Making of National Economic Forecasts, (pp. 319–351). Edward Elgar: Cheltenham. [doi:10.4337/9781849802161.00017]
HABER, G. (2008). Monetary and fiscal policies analysis with an agent-based macroeconomic model. Journal of Economics and Statistics, 228, 276–295. [doi:10.1515/jbnst-2008-2-308]
HALDANE, A. (2012). The dog and the frisbee. Central bankers’ speeches, BIS.
HARTING, P. (2015). Stabilization policies and long term growth: Policy implications from an agent-based macroeconomic model. Tech. Rep. 06-2015, Bielefeld Working Papers in Economics and Management. [doi:10.2139/ssrn.2620145]
HENDRY, D. & Minzon, G. (2010). On the mathematical basis of inter-temporal optimization. Economics Series Working Papers 497, University of Oxford.
HOWITT, P. (1992). Interest rate control and nonconvergence to rational expectations. Journal of Political Economy, 100, 776–800. [doi:10.1086/261839]
HOWITT, P. (2011). What have central bankers learned from modern macroeconomic theory? Journal of Macroeconomics, 34 (1), 11–22. [doi:10.1016/j.jmacro.2011.08.005]
ISAAC, A. G. (2014). The intergenerational propagation of wealth inequality. Metroeconomica, 65, 571–584. [doi:10.1111/meca.12057]
ISLEY, S., Lempert, R., Popper, S. & Vardavas, R. (2013). An evolutionary model of industry transformation and the political sustainability of emission control policies. Tech. rep., RAND Corporation.
JOHANSEN, S. (2006). Confronting the economic model with the data. In D. Colander (Ed.), Post Walrasian Macroeconomics. Cambridge, Cambridge University Press. [doi:10.1017/cbo9780511617751.017]
JOHANSEN, S. & Juselius, K. (2006). ‘Extracting information from the data: A European view on empirical macro’. In D. Colander (Ed.), Post Walrasian Macroeconomics. Cambridge, Cambridge University Press.
JUSELIUS, K. & Franchi, M. (2007). Taking a DSGE model to the data meaningfully. Economics: The Open-Access, Open-Assessment E-Journal, 1(2007-4).
KAHNEMAN, D. & Tversky, A. (Eds.) (2000). Choices, Values, and Frames. Cambridge MA, Cambridge University Press.
KAY, J. (2011). The map is not the territory: An essay on the state of economics. Tech. rep., Institute for New Economic Thinking.
KEYNES, J. M. (1936). The General Theory of Employment, Interest, and Money. New York, Prometheus Books.
KEYNES, J. M. (1937). The general theory of employment. Quarterly Journal of Economics, 51, 209–223. [doi:10.2307/1882087]
KIRMAN, A. P. (1989). The intrinsic limits of modern economic theory: the emperor has no clothes. Economic Journal, 99, 126–39. [doi:10.2307/2234075]
KIRMAN, A. P. (1992). Whom or what does the representative individual represent? Journal of Economic Perspectives, 6, 117–136. [doi:10.1257/jep.6.2.117]
KIRMAN, A. P. (2010). The economic crisis is a crisis for economic theory. CESifo Economic Studies, 56, 498–535. [doi:10.1093/cesifo/ifq017]
KIRMAN, A. P. (2016). Ants and nonoptimal self-organization: Lessons for macroeconomics. Macroeconomic Dynamics, 20(2), 601-621. [doi:10.1017/S1365100514000339]
KLIMEK, P., Poledna, S., Farmer, D. J. & Thurner, S. (2015). To bail-out or to bail-in? Answers from an agent-based model. Journal of Economic Dynamics & Control, 50, 144–154. [doi:10.1016/j.jedc.2014.08.020]
KNIGHT, F. (1921). Risk, Uncertainty, and Profits. Chicago, Chicago University Press.
KRAUSE, A. & Giansante, S. (2012). Interbank lending and the spread of bank failures: A network model of systemic risk. Journal of Economic Behavior & Organization, 83, 583–608. [doi:10.1016/j.jebo.2012.05.015]
KRUG, S. (2015). The interaction between monetary and macroprudential policy: Should central banks "lean against the wind" to foster macro-financial stability? Economics Working Paper 2015-08, Christian-Albrechts-University of Kiel.
KRUG, S., Lengnick, M. & Wohltman, H.-W. (2015). The impact of BASEL III on financial (in)stability: An agent-based credit network approach. Quantitative Finance, 15, 1917–1932. [doi:10.1080/14697688.2014.999701]
KRUGMAN, P. (2009). How did economics get it so wrong? New York Times Magazine, (9), 36–44.
KRUGMAN, P. (2011). The profession and the crisis. Eastern Economic Journal, 37, 307–312. [doi:10.1057/eej.2011.8]
KRUSEL, P. & Smith, A. A. (1998). Income and wealth heterogeneity in the macroeconomy. Journal of Political Economy, 106, 867–896. [doi:10.1086/250034]
KUMHOF, M., Ranciere, R. & Winant, P. (2015). Inequality, leverage, and crises. American Economic Review, 105, 1217–45. [doi:10.1257/aer.20110683]
LAMPERTI, F. (2015). An information theoretic criterion for empirical validation of time series models. LEM papers series, Laboratory of Economics and Management (LEM), Scuola Superiore Sant’Anna, Pisa, Italy. [doi:10.2139/ssrn.2570828]
LAMPERTI, F. (2016). Empirical validation of simulated models through the GSL-div: an illustrative application. LEM Papers Series 2016/18, Laboratory of Economics and Management (LEM), Scuola Superiore Sant’Anna, Pisa, Italy.
LAMPERTI, F., Dosi, G., Napoletano, M., Roventini, A. & Sapio, S. (2016a). Faraway, so close: An agent-based model for climate, energy and macroeconomic policies. Working paper series forthcoming, Laboratory of Economics and Management (LEM), Scuola Superiore Sant’Anna, Pisa, Italy.
LAMPERTI, F., Sani, A., Mandel, A. & Roventini, A. (2016b). Agent based model exploration and calibration using machine learning surrogates. Working Paper Series forthcoming, Laboratory of Economics and Management (LEM), Scuola Superiore Sant’Anna, Pisa, Italy.
LANE, D. A. (1993). Artificial worlds and economics, part I and II. Journal of Evolutionary Economics, 3, 89–107 and 177–197. [doi:10.1007/bf01200867]
LEBARON, B. & Tesfatsion, L. (2008). Modeling macroeconomies as open-ended dynamic systems of interacting agents. American Economic Review, 98, 246–250. [doi:10.1257/aer.98.2.246]
LENGNICK, M., Krug, S. & Wohltman, H.-W. (2013). Money creation and financial instability: An agent-based credit network approach. Economics: The Open-Access, Open-Assessment E-Journal, 7, 2013–2032
LENGNICK, M. & Wohltman, H.-W. (2016). Optimal monetary policy in a new Keynesian model with animal spirits and financial markets. Journal of Economic Dynamics & Control, 64, 148–165.
LINDÉ, Smets, F. & Wouters, R. (2016). ‘Challenges for central banks’ macro models’. In J. B. Taylor & H. Uhlig (Eds.), Handbook of Macroeconomics. North Holland. [doi:10.1016/bs.hesmac.2016.04.009]
LINDLEY, D. (1994). The End of Physics. Basic Books. [doi:10.1007/978-3-0348-6193-9]
MANDEL, A., Jaeger, C., Fuerst, S., Lass, W., Lincke, D., Meissner, F., Pablo-Marti, F. & Wolf, S. (2010). Agent-based dynamics in disaggregated growth models. Working Paper 2010.77, CES.
MANKIW, G. N. (2006). The macroeconomist as scientist and engineer. Journal of Economic Perspectives, 20, 29–46. [doi:10.1257/jep.20.4.29]
MANTEL, R. (1974). On the characterization of aggregate excess demand. Journal of Economic Theory, 7, 348–353. [doi:10.1016/0022-0531(74)90100-8]
MASSARO, D. (2013). Heterogeneous expectations in monetary DSGE models. Journal of Economic Dynamics & Control, 37, 680–692. [doi:10.1016/j.jedc.2012.11.001]
MEHRLING, P. (2006). ‘The problem of time in the DSGE model and the post Walrasian alternative’. In D. Colander (Ed.), Post Walrasian Macroeconomics. Cambridge, Cambridge University Press. [doi:10.1017/cbo9780511617751.005]
MISHKIN, F. S. (2007). Will monetary policy become more of a science? Working Paper 13566, NBER.
MITTNIK, S. & Semmler, W. (2013). The Real Consequences of Financial Stress. Journal of Economic Dynamics & Control, 37(8), 1479–1499. [doi:10.1016/j.jedc.2013.04.014]
MONASTEROLO, I. & Raberto, M. (2016). A hybrid system dynamics – agent based model to assess the role of green fiscal and monetary policies. Tech. rep., SSRN. [doi:10.2139/ssrn.2748266]
MOSS, S. (2008). Alternative approaches to the empirical validation of agent-based models. Journal of Artificial Societies and Social Simulation, 11(1) 5: https://www.jasss.org/11/1/5.html.
MUTH, J. F. (1961). Rational expectations and the theory of price movements. Econometrica, 29(315-335). [doi:10.2307/1909635]
NAPOLETANO, M., Dosi, G., Fagiolo, G. & Roventini, A. (2012). Wage formation, investment behavior and growth regimes: An agent-based analysis. Revue de l’OFCE, 124, 235–261. [doi:10.3917/reof.124.0235]
NAPOLETANO, M., Gaffard, J.-L. & Roventini, A. (2015). Time-varying fiscal multipliers in an agent-based model with credit rationing. Working Paper Series 2015/19, Laboratory of Economics and Management (LEM), Scuola Superiore Sant’Anna, Pisa, Italy.
NELSON, R. R. & Winter, S. G. (1982). An Evolutionary Theory of Economic Change. Cambridge, The Belknap Press of Harvard University Press.
ORMEROD, P. (2004). Information cascades and the distribution of economic recessions in capitalist economies. Physica A, 341, 556–568. [doi:10.1016/j.physa.2004.04.109]
ORMEROD, P. (2010). Risk, recessions and the resilience of the capitalist economies. Risk Management, 12, 83–99. [doi:10.1057/rm.2009.3]
ORPHANIDES, A. & Williams, J. C. (2008). Robust monetary policy with imperfect knowledge. Journal of Monetary Economics, 54, 1406–1435. [doi:10.1016/j.jmoneco.2007.06.005]
PESARAN, H. M. & Chudik, A. (2011). Aggregation in large dynamic panels. Working Paper Series 3346, CESifo.
PIKETTY, T. & Zucman, G. (2014). Capital is back: Wealth-income ratios in rich countries, 1700-2010. Quarterly Journal of Economics, 129, 1155–1210. [doi:10.1093/qje/qju018]
PINDYCK, R. (2013). Climate change policy: What do the models tell us? Journal of Economic Literature, 51, 860–872. [doi:10.1257/jel.51.3.860]
POLEDNA, S., Thurner, S., Farmer, D. J. & Geanakoplos, J. (2014). Leverage-induced systemic risk under BASEL II and other credit risk policies. Journal of Banking & Finance, 42, 199–2012. [doi:10.1016/j.jbankfin.2014.01.038]
POPOYAN, L., Napoletano, M. & Roventini, A. (2015). Taming macroeconomic instability: Monetary and macro prudential policy interactions in an agent-based model. Working Paper Series 2015/33, Laboratory of Economics and Management (LEM), Scuola Superiore Sant’Anna, Pisa, Italy.
POUDYAL, N. & Spanos, A. (2013). Confronting theory with data: Model validation and DSGE modeling. Working paper, Department of Economics, Virginia Tech, USA.
PYKA, A. & Fagiolo, G. (2007). ‘Agent-based modelling: A methodology for neo-Schumpeterian economics’. In H. Hanusch & A. Pyka (Eds.), The Elgar Companion to Neo-Schumpeterian Economics. Cheltenham, Edward Elgar Publishers. [doi:10.4337/9781847207012.00037]
PYKA, A. & Werker, C. (2009). The methodology of simulation models: Chances and risks. Journal of Artificial Societies and Social Simulation, 12 (4) 1: https://www.jasss.org/12/4/1.html.
RABERTO, M., Teglio, A. & Cincotti, S. (2008). Integrating real and financial markets in an agent-based economic model: An application to monetary policy design. Computational Economics, 32, 147-162.
RABERTO, M., Teglio, A. & Cincotti, S. (2012). Debt deleveraging and business cycles. An agent-based perspective. Economics - The Open-Access, Open-Assessment E-Journal, 6(1-49). [doi:10.5018/economics-ejournal.ja.2012-27]
RAVENNA, F. (2007). Vector autoregressions and reduced form representations of DSGE models. Journal of Monetary Economics, 54, 2048–2064. [doi:10.1016/j.jmoneco.2006.09.002]
RECCHIONI, M. C., Tedeschi, G. & Gallegati, M. (2015). A calibration procedure for analyzing stock price dynamics in an agent-based framework. Journal of Economic Dynamics & Control, 60, 1–25. [doi:10.1016/j.jedc.2015.08.003]
RENGS, B. & Wackerle, M. (2014). A computational agent-based simulation of an artificial monetary union for dynamic comparative institutional analysis. In Proceedings of the 2014 IEEE Conference on Computational Intelligence for Financial Engineering & Economics, (pp. 427–434). [doi:10.1109/CIFEr.2014.6924105]
RENGS, B., Wackerle, M., Gazheli, A., Antal, M. & van den Bergh, J. (2015). Testing innovation, employment and distributional impacts of climate policy packages in a macro-evolutionary systems setting. Working paper 83, WWWforEurope.
RICCETTI, L., Russo, A. & Gallegati, M. (2013a). Leveraged network-based financial accelerator. Journal of Economic Dynamics & Control, 37, 1626–1640. [doi:10.1016/j.jedc.2013.02.008]
RICCETTI, L., Russo, A. & Gallegati, M. (2013b). Unemployment benefits and financial leverage in an agent based macroeconomic model. Economics: The Open-Access, Open-Assessment E-Journal, 7, 2013–2042.
RICCETTI, L., Russo, A. & Gallegati, M. (2014). An agent based decentralized matching macroeconomic model. Journal of Economic Interaction and Coordination, 10, 305–332. [doi:10.1007/s11403-014-0130-8]
RICHIARDI, M., Leombruni, R., Saam, N. J. & Sonnessa, M. (2006). A common protocol for agent-based social simulation. Journal of Artificial Societies and Social Simulation, 9(1) 15: https://www.jasss.org/9/1/15.html.
ROBALINO, D. & Lempert, R. (2000). Carrots and sticks for new technology: Abating greenhouse gas emissions in a heterogeneous and uncertain world. Integrated Assessment, 1, 1–19. [doi:10.1023/A:1019159210781]
ROMER, P. (2016). The trouble with macroeconomics. The American Economist, forthcoming.
ROSSER, B. J. (2011). Complex Evolutionary Dynamics in Urban-Regional and Ecologic-Economic Systems: From Catastrophe to Chaos and Beyond. Springer: New York. [doi:10.1007/978-1-4419-8828-7]
ROTEMBERG, J. & Woodford, M. (1999). Interest rate rules in an estimated sticky price model. In J. Taylor (Ed.), Monetary Policy Rules. University of Chicago Press: Chicago.
RUSSO, A., Catalano, M., Gallegati, M., Gaffeo, E. & Napoletano, M. (2007). Industrial dynamics, fiscal policy and R&D: Evidence from a computational experiment. Journal of Economic Behavior & Organization, 64, 426–447. [doi:10.1016/j.jebo.2006.06.016]
RUSSO, R. L., A. & Gallegati, M. (2016). Increasing inequality, consumer credit and financial fragility in an agent based macroeconomic model. Journal of Evolutionary Economics, 26, 25–47. [doi:10.1007/s00191-015-0410-z]
SAARI, D. & Simon, C. P. (1978). Effective price mechanisms. Econometrica, 46, 1097–1125. [doi:10.2307/1911438]
SALLE, I. (2015). Modeling expectations in agent-based models - An application to Central Bank’s communication and monetary policy. Economic Modelling, 46, 130–141. [doi:10.1016/j.econmod.2014.12.040]
SALLE, I. & Yıldızoğlu, M. (2014). Efficient sampling and meta-modeling for computational economic models. Computational Economics, 44(4), 507–536. [doi:10.1007/s10614-013-9406-7]
SALLE, I., Yıldızoğlu, M. & Senegas, M.-A. (2013). Inflation targeting in a learning economy: An ABM perspective.Economic Modelling, 34, 114–128. [doi:10.1016/j.econmod.2013.01.031]
SCHLEFER, J. (2012). The Assumptions Economists Make. Harvard, Harvard University Press. [doi:10.4159/harvard.9780674065529]
SCHMITT-GROHÉ, S. & Uribe, M. (2000). Price level determinacy and monetary policy under a balanced-budget requirement. Journal of Monetary Economics, 45, 211–246. [doi:10.1016/S0304-3932(99)00046-X]
SCHORFHEIDE, F. (2008). DSGE model-based estimation of the new Keynesian Philips curve. FRB Richmond Economic Quarterly, Fall Issue, 397–433.
SEPPECHER, P. (2012). Flexibility of wages and macroeconomic instability in an agent-based computational model with endogenous money. Macroeconomic Dynamics, 16, 284–297. [doi:10.1017/S1365100511000447]
SEPPECHER, P. & Salle, I. (2015). Deleveraging crises and deep recessions: A behavioural approach. Applied Economics, 47, 3771–3790. [doi:10.1080/00036846.2015.1021456]
SETTERFIELD, M. (2016). Won’t get fooled again – or will we? Monetary policy, model uncertainty, and ‘policy model complacency’. Working Papers 1516, New School for Social Research, Department of Economics.
SINITSKAYA, E. & Tesfatsion, L. (2015). Macroeconomies as Constructively Rational Games. Journal of Economic Dynamics & Control, 61(C), 152–182. [doi:10.1016/j.jedc.2015.09.011]
SMETS, F. & Wouters, R. (2003). An estimated dynamic stochastic general equilibrium model of the Euro area. Journal of the European Economic Association, 1, 1123–1175. [doi:10.1162/154247603770383415]
SMETS, F. & Wouters, R. (2007). Shocks and frictions in us business cycles: A Bayesian DSGE approach. American Economic Review, 97, 586–606. [doi:10.1257/aer.97.3.586]
SMITH, N. (2014). Wall Street skips economics class. BlombergView.
SNOWDON, B. & Vane, H. R. (2005). Modern Macroeconomics: Its Origins, Development and Current State. Edward Elgar: Cheltenham.
SONNENSCHEIN, H. (1972). Market excess demand functions. Econometrica, 40, 549–556. [doi:10.2307/1913184]
STIGLITZ, J. (2011). Rethinking macroeconomics: What failed, and how to repair it. Journal of the European Economic Association, 9, 591–645. [doi:10.1111/j.1542-4774.2011.01030.x]
STIGLITZ, J. (2015). Towards a general theory of deep downturns. Working Paper 21444, NBER. [doi:10.3386/w21444]
SUMMERS, L. (1991). The scientific illusion in empirical macroeconomics. Scandinavian Journal of Economics, 93(2), 129–148 [doi:10.2307/3440321]
TAYLOR, J. (1993). Discretion versus policy rules in practice. Carnegie-Rochester Series on Public Policy, 39, 195–214.
TAYLOR, J. (2007). The explanatory power of monetary policy rules. Working Paper 13685, NBER. [doi:10.3386/w13685]
TAYLOR, J. B. & Williams, J. C. (2010). Simple and robust rules for monetary policy. In B. M. Friedman & M. Woodford (Eds.), Handbook of Monetary Economics, vol. 3. Elsevier: Amsterdam. [doi:10.3386/w15908]
TEGLIO, A., Mazzocchetti, A., Ponta, L., Raberto, M. & Cincotti, S. (2015). Budgetary rigour with stimulus in lean times: Policy advices from an agent-based model. Working Papers 2015/07, Economics Department, Univesitat Jaume I, Castellón (Spain).
TESFATSION, L. (2006a). Ace: A constructive approach to economic theory. In L. Tesfatsion & K. Judd (Eds.), Handbook of Computational Economics II: Agent-Based Computational Economics. Amsterdam, North Holland. [doi:10.1016/S1574-0021(05)02016-2]
TESFATSION, L. (2006b). ‘Agent-based computational modeling and macroeconomics’. In D. Colander (Ed.), Post Walrasian Macroeconomics. Cambridge, Cambridge University Press. [doi:10.1017/CBO9780511617751.011]
TESFATSION,L. & Judd, K. (Eds.) (2006). Handbook of Computational Economics II: Agent-Based Computational Economics. North Holland, Amsterdam.
VAN der Hoog, S. (2015). The limits to credit growth: Mitigation policies and macroprudential regulations to foster macrofinancial stability and sustainable debt. Working Papers in Economics and Management 08-15, University of Bielefeld. [doi:10.2139/ssrn.2673402]
VAN der Hoog, S. & Dawid, H. (2015). Bubbles, crashes and the financial cycle: Insights from a stock-flow consistent agent-based macroeconomic model. Working Papers in Economics and Management 01-2015, University of Bielefeld.
WINKER, P., Gilli, M. & Jeleskovic, V. (2007). An objective function for simulation based inference on exchange rate data. Journal of Economic Interaction and Coordination, 2, 125–145. [doi:10.1007/s11403-007-0020-4]
WOLF, S., Bouchaud, J.-P., Cecconi, F., Cincotti, S., Dawid, H., Gintis, H., van der Hoog, S., Jaeger, C. C., Kovalevsky, D. V., Mandel, A. & Paroussos, L. (2013a). Describing economic agent-based models. Dahlem ABM documentation guidelines. Complexity Economics, 2, 63–74. [doi:10.7564/13-COEC12]
WOLF, S., Furst, S., Mandel, A., Lass, W., Lincke, D., Pablo-Marti, F. & Jaeger, C. (2013b). A multi-agent model of several economic regions. Environmental Modelling & Software, 44, 25–43. [doi:10.1016/j.envsoft.2012.12.012]
WOODFORD, M. (1990). Learning to believe in sunspots. Econometrica, 58, 277–307. [doi:10.2307/2938205]
WOODFORD, M. (2003). Interest and Prices: Foundations of a Theory of Monetary Policy. Princeton, NJ, Princeton University Press.
WOODFORD, M. (2009). Convergence in macroeconomics: Elements of the new synthesis. American Economic Journal: Macroeconomics, 1, 267–279. [doi:10.1257/mac.1.1.267]
WOODFORD, M. (2010). Optimal monetary stabilization policy. In B. M. Friedman & M. Woodford (Eds.), Handbook of Monetary Economics, vol. 3. Elsevier: Amsterdam. [doi:10.3386/w16095]
WREN-LEWIS, S. (2016). Unravelling the New Classical Counter Revolution. Review of Keynesian Economics, 4(1), 20–35. [doi:10.4337/roke.2016.01.03]
ZARNOWITZ, V. (1985). Recent works on business cycles in historical perspectives: A review of theories and evidence. Journal of Economic Literature, 23, 523–80.
ZARNOWITZ, V. (1997). Business cycles observed and assessed: Why and how they matter. Working Paper 6230, NBER. [doi:10.3386/w6230]
