Asynchronous Opinion Dynamics with Online and Offline Interactions in Bounded Confidence Model

Zhaogang Ding; Yucheng Dong; Haiming Liang; Francisco Chiclana

doi:10.18564/jasss.3375

Introduction

Opinion dynamics is a research tool widely used to investigate the opinion evolution in many collective phenomena. The study of opinion formation goes back as far as French (1956). Following French’s study, some opinion dynamics models based on different communication regimes had been proposed, such as DeGroot model (DeGroot 1974; Berger 1981), Friedkin and Johnsen model (Friedkin & Johnsen 1990) and bounded confidence model (Deffuant & Weisbuch 2000; Hegselmann & Krause 2002).

Among these opinion dynamics models, the bounded confidence model has been frequently used in recent years. The bounded confidence model assumes all agents are bounded confident, i.e. each agent updates her/his opinion by averaging the agents’ opinions that differ from his/her own no more than a certain confidence level. In the Deffuant & Weisbuch model (i.e., DW model), agents follow a pairwise-sequential updating mechanism, while in the Hegselmann & Krause model (i.e., HK model), each agent updates his/her opinion by averaging all opinions in their confidence sets. In other words, the DW model and the HK model are very similar but differ mainly in the communication regime (Urbig et al. 2008). Following the DW and HK models, some interesting extended studies have been conducted (Dong et al. 2016; Weisbuch 2004; Fortunato et al., 2005; Lorenz 2006; Morarescu & Girard 2011; Ceragioli & Frasca 2012; Liang et al. 2016; Mathias et al. 2016).

In most existing opinion dynamics models, all agents update their opinions at the same time according to the established rules, i.e. the evolution of opinions is synchronous. The general theory of asynchronous systems has been supported in the specialized literature (Bertsekas & Tsitsiklis 1989; Chen et al., 2015; Dong & Zhang 2014; Frommer & Szyld 2000; Kozyakin 2003). Particularly, Alizadeh & Cioffi-Revilla (2015) studied the asynchronous updating schemes in the bounded confidence model in an elegant and concise way. They applied four different asynchronous updating schemes including random, uniform, and two state-driven Poisson updating schemes, and compared the effect of different activation regimes (i.e. the timing of activation).

With the development of the Information and Internet technology, asynchronization prevails in online and offline interactions. According to eMarketer Report (2016), about half of the population now can receive information and exchange opinions with others in an online environment (e.g. the Internet), while the other preferably search and share information offline (e.g. face to face). The Internet technologies (e.g. Facebook, Myspace, etc.) enable online agents to spread and share information in a more rapid way than offline agents (Bakshy et al. 2012; Song and Yan, 2012; Zhao et al. 2011). For the above reasons, in this paper we consider online and offline as two subsystems in opinion dynamics, and assume that there is an asynchronization when agents in these two subsystems update their opinions. Then, based on the HK bounded confidence model, we investigate the opinion dynamics with asynchronous interactions between online and offline agents. We focus on how asynchronization in online and offline interactions affects the dynamics of opinion formation.

Through extensive agent-based simulations and analyses, we unveil that asynchronization in online and offline interactions has a strong impact on the dynamics of opinion formation. Specifically, asynchronization lengthens the steady-state time of opinion evolution, and leads to the absorption phenomena between the online and offline subsystems.

The remainder of this paper is as follows. Section 2 introduces the HK bounded confidence model. Section 3 then proposes the asynchronous opinion dynamics model with online and offline interactions in the framework of bounded confidence. Next, Section 4 discusses the influences of asynchronism and the size of the online subsystem in the proposed model. Finally, Section 5 presents the concluding remarks.

The Hegselmann & Krause Bounded Confidence Model

In this section, we briefly introduce the HK bounded confidence model. Since the DW model and the HK model are rather similar, if we adopt the DW model as the basic model, a similar asynchronous opinion dynamics model will be conducted.

Let $A=\{1,2,\dots,N\}$ be a set of the agents. Let $x_i^t\in [0,1]$ be the opinion of agent $i$ at time $t$, and thus $X^t=(x_1^t,\dots,x_i^t,\dots,x_N^t)^T$ be the opinion profile at time $t$. Let $\epsilon$ be the homogeneous confidence level of the agents.

The process of the HK model consists of three steps. The first is to determine the confidence set. The confidence set $I(i,X^t)$ of the agent $i$ at time $t$ is determined as:

$$I(i,X^t)=\Bigl\{ j | \Big\lvert x_i^t - x_j^t \Big\rvert \leq \epsilon \Bigr\}$$

(1)

Then, the second step is to calculate of the weights that one agent assigns to other agents. Let $w_{ij}^t$ be the weight of agent $i$ assigns to agent $j$ at time $t$, i.e.,

$$w_{ij}^t= \begin{cases}\frac{1}{\#I(i,X^t)}, &\hspace {-0.4cm} \quad j\in I(i,X^t)\\ 0, &\hspace {-0.4cm} \quad j\notin I(i,X^t)\end{cases}$$

(2)

where $\#I(i,X^t)$ denotes the number of agents in the confidence set $I(i,X^t)$

Finally, the third step is to determine the updated opinions for each agent. The updated opinion $x_i^{t+1}$ is modeled as a weighted arithmetic mean of opinions in the confidence set, i.e.,

$$x_i^{t+1}=\sum_{j=1}^N w_{ij}^t x_j^t$$

(3)

The Asynchronous Opinion Dynamics Model in Online and Offline Interactions

In this section, we propose the asynchronous opinion dynamics model in online and offline interactions based on the HK bounded confidence model. In the same way as the HK model in Section 2, $A=\{1,2,\dots,N\}$ be a set of agents, $x_i^t\in [0,1]$ be the opinion of agent $i$ at time $t$, and $\epsilon$ be the homogeneous confidence level of the agents.

In the proposed model, agents are divided into two types: the online and the offline agents. All online agents constitute the online subsystem and all offline agents constitute the offline subsystem. For the sake of simplicity, let $A^{on}$ be the set of online agents and $A^{off}$ be the set of offline agents, where $A^{on}\cup A^{off}=A$ and $A^{on}\cap A^{off}=\emptyset$.

Based on existing studies (Bakshy et al. 2012; Song and Yan 2012; Zhao et al. 2011), we assume that the speed of updating opinions for the online agents is much faster than that for the offline agents, and let $T$ be the degree of asynchronization between the online and offline subsystems, where $T=1$ and $T\in N$. Then, let $T^{on}=\{0,1,2,\dots\}$ and $T^{off}=\{0,T,2T,\dots\}$ be two sets of discrete time, where $T^{off}\subseteq T^{on}$. When time $t\in T^{on}$ and $t\notin T^{off}$, only the online agents will update their opinions, and when $t\in T^{off}$, both the online and offline agents will update their opinions. And thus $T=1$ represents synchronization and $T≥2$ asynchronization. Obviously, the larger the $T$ value is, the more asynchronization between agents in online and offline subsystems.

Next, we propose the asynchronous opinion dynamics model with online and offline interactions in the framework of bounded confidence based on the following two cases:

Case A: $t+1\in T^{on}$ and $t+1\notin T^{off}$. In this case, for any agent $i$ in $A^{on}$, he/she only communicates with other online agents at time $t$. The confidence set $I^A(i,X^t)$ of the agent $i\in A^{on}$ is determined as:

$$I^A(i,X^t) = \Bigl\{ j | \Big \lvert x_i^t-x_j^t \Big \rvert \leq \epsilon, \, j \in A^{on} \Bigr\}$$ (4)
Then, the weight $w_{ij}^t$ of agent $i$ assigns to agent $j$ at time $t$ can be calculated as:

$$w_{ij}^t= \begin{cases} \frac{1}{\#I^A(i,X^t)}, & j\in I^A(i,X^t)\\ 0, & j\notin I^A(i,X^t) \end{cases}$$ (5)
In addition, any agent $i\in A^{off}$, he/she does not communicate with other agents at time $t$ and thus he/she will not update his/her opinion at time $t+1$, i.e. $x_i^{t+1}=x_i^t$. Above all, in this case, the updated opinion $x_i^{t+1}$ is calculated as:

$$x_i^{t+1}= \begin{cases} \sum_{j=1}^N w_{ij}^t x_j^t, & i\in A^{on}\\ x_i^t, & i\in A^{off} \end{cases}$$ (6)

Case B: $t+1\in T^{on}$ and $t+1\in T^{off}$. In this case, the agent $i\in A$ can communicate with both the online and offline agents at time $t$. Thus, the confidence set $I^B(i,X^t)$ is determined as:

$$I^B(i,X^t)=\Bigl\{j|\Big\lvert x_i^t-x_j^t\Big\rvert\leq\epsilon,\,j\in A \Bigr\}$$

(7)

Then, the weight $w_{ij}^t$ of agent $i$ assigns to agent $j$ at time $t$ is determined as:

$$w_{ij}^t= \begin{cases} \frac{1}{\#I^B(i,X^t)}, & j\in I^B(i,X^t)\\ 0, & j\notin I^B(i,X^t) \end{cases}$$

(8)

In this case, the updated opinion $x_i^{t+1}$ is calculated as:

$$x_i^{t+1}=\sum_{j=1}^N w_{ij}^t x_j^t$$

(9)

Based on Cases A and B, for any agent $i$ at time $t+1\in T^{on}$, the updated opinion $x_i^{t+1}$ is calculated as:

$$x_i^{t+1}= \begin{cases} \sum_{j=1}^N w_{ij}^t x_j^t, & i\in A^{on},\,t+1\notin T^{off}\\ x_i^t, & i\in A^{off},\,t+1\notin T^{off}\\ \sum_{j=1}^N w_{ij}^t x_j^t, & t+1\in T^{off}\end{cases}$$

(10)

where $w_{ij}^t$ is determined by Equations 4 and 5 in the case of $i\in A^{on}$ and $t+1\notin T^{off}$, or is determined by Equations 7 and 8 in the case of $i\in A$ and $t+1\in T^{off}$

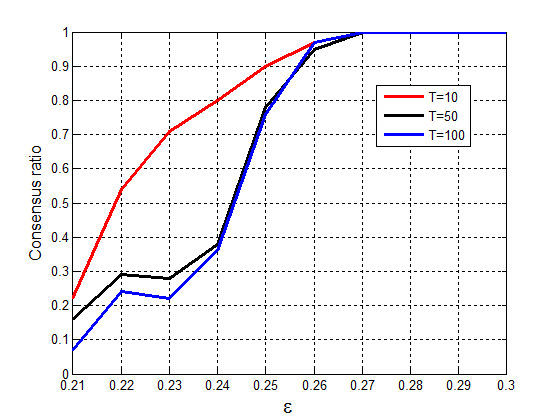
Similar to the HK model, the confidence level $\epsilon$ plays a key role in our model. We set $N$ = 1000, with half being online agents and the other half offline agents, and the initial opinions of all agents are uniformly and randomly distributed in [0,1]. We use Equation 10 to proceed with the evolution of opinions, and analyze the steady-state consensus ratio from 1000 independent realizations. As shown in Figure 1, the consensus ratio increases under different $T$ values, when the $\epsilon$ value increases. In Figure 1 we can clearly see that all agents can almost surely reach a consensus if the $\epsilon$ value is larger than 0.27 under different $T$ values.

**Figure 1**. The steady-state consensus ratio under different ε and T values from 1000 independent realizations.

The Influence of Asynchronism in the Opinion Formation

In this section, we focus on how asynchronization impacts the dynamics of opinion formation in online and offline contexts based on six criteria, the steady-state time, the number of opinion clusters, the number of pure online/offline opinion clusters and the absorption of the online /offline subsystem.

The steady-state time $T^*$ is defined as the minimum time it takes all agents' opinions to reach a stable state. The results regarding the steady-state time $T^*$ are included in Appendix A.
The opinion clusters appear when the steady-state is finally reached in opinion dynamics. The number of opinion clusters $S_{NC}$ is defined as the number of different opinion clusters among the agents in the stable state. Larger $S_{NC}$ values indicate more different opinions among the agents in the stable state. In particular, $S_{NC} =1$ indicates all agents reach a consensus finally.
The pure online opinion cluster is defined as an opinion cluster in which all agents are online agents, and the pure offline opinion cluster is defined as an opinion cluster in which all agents are offline agents. $S_{NPC}^{on}$ and $S_{NPC}^{off}$ denote the number of pure online opinion clusters and pure offline opinion clusters in the stable state, respectively.
The absorption of the online subsystem is defined as the capacity that the online subsystem attracts the offline agents, and the absorption of the offline subsystem is defined as the capacity that the offline subsystem attracts the online agents. In this paper, $L^{on}$ and $L^{off}$ are the indexes to measure the absorption of the online subsystem and the offline subsystem in the stable state, respectively. The formal definitions $L^{on}$ and $L^{off}$ are in Sections 4.10 and 4.11.

Let $p=\# A^{on} / \# A$ be the percentage of the online agents in all agents, denoting the size of the online subsystem. Without loss of generality, we assume that the former $N \times p$ agents (i.e., $i\in \{1,2,\dots,N\times p\}$) are the online agents and the latter $N\times (1-p)$ agents (i.e., $i\in \{N\times p+1,N\times p+2,\dots,N\}$) are offline agents. We set $N=1000$, the initial opinions of all agents are uniformly and randomly distributed in $[0,1]$. In addition, the homogeneous confidence level of the agents $\epsilon$ is selected in $[0, 0.3]$. Then, using Equation 10 proceeds with the evolution of opinions, obtaining the average $T^*$, $S_{NC}$, $S_{NPC}^{on}$, $S_{NPC}^{off}$, $L^{on}$ and $L^{off}$ values under different $T$, $p$ and $\epsilon$ values from 1000 independent realizations.

In the simulation, when $\|X^{t+1}-X^t\|\leq\delta$, we consider that the opinions of all agents reach the stable state, where $\|X\|=\max_{1\leq i\leq n}{|x_i|}$, and we set $\delta=10^{-3}$. Notice that a different norm of the vector $X$, such as $\|X\|=\sum_{i=1}^n|x_i|$, does not influence the main results in this paper. Meanwhile, let $x_i,x_j$ be the opinions of agents $i,j$ when the opinions reach the stable state. We assign the agents $i,j$ to a same cluster when $|x_i-x_j|<d$, and we set $d=10^{-2}$ (the pseudo-code of calculating opinion clusters is included in Appendix B).

Although we only represent the results when $T\in [1,100]$ and $N=1000$ in the paper, the results are similar when setting $T>100$ and different $N$ values (e.g., $N$ =500, 2000 and 3000).

The number of opinion clusters

Figure 2 illustrates how the number of opinion clusters changes along with the confidence level and the degree of asynchronization. Increasing the confidence level yields an increase in communication among the agents, this translates to a decrease of the number of opinion clusters. Meanwhile, the number of opinion clusters increases as $T$ increases from $T=1$ to $T=10$, and such an effect is more evident for the large size of online agents ($p$=80%) and for low confidence levels. The asynchronization delays the update time of offline agents, and thus the agents will form more opinion clusters because of fewer communications between the online and offline agents. However, with further increments of $T$, the evolution of online agents’ opinions will rapidly reach a stable state among them before the offline agents start to update opinions, which stops the increase of the number of opinion clusters.

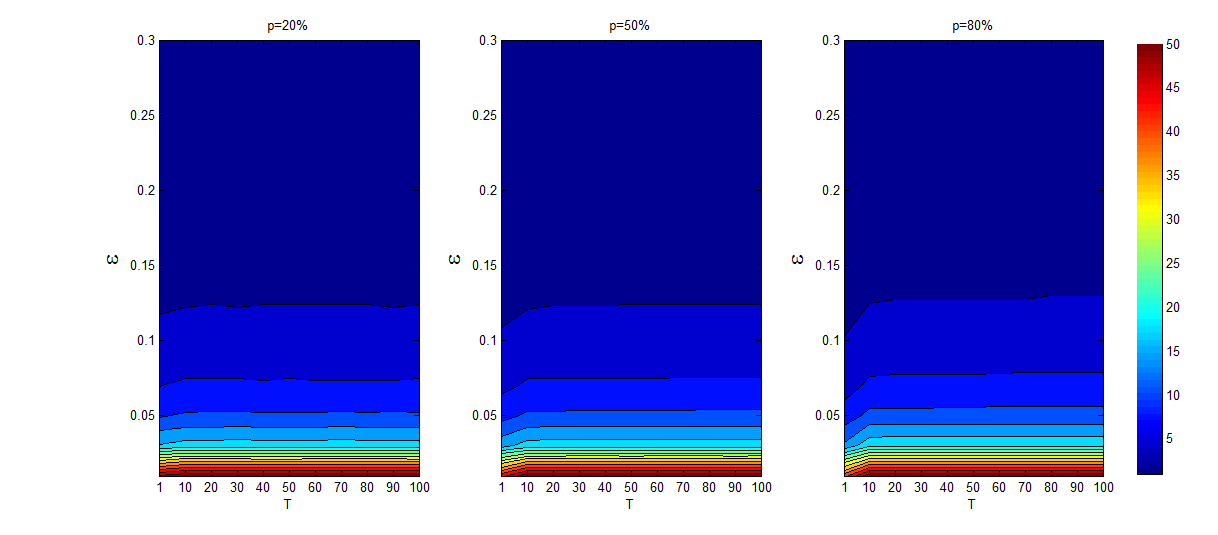
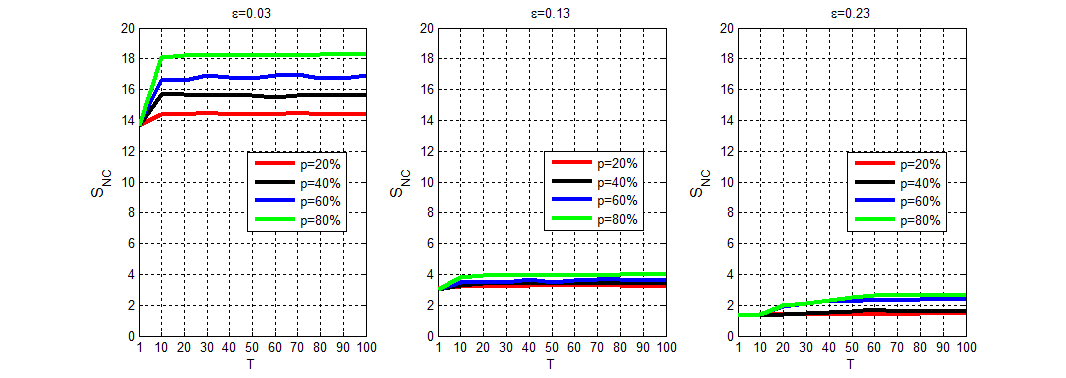
**Figure 2**. The average *S_NC* values under different T and ε values from 1000 independent realizations, where T∈[1,100].

Figure 3 further helps understanding the impact of the size of online agents on the number of opinion clusters. Figure 3 clearly indicates that a large size of online agents leads to a large number of opinion clusters, and such an effect is more evident for $T=10$. On the one hand, online agents cluster faster than offline agents, with online agents rapidly reaching a steady-state in general when $T=10$, and thus the communications between online and offline agents barely change when $T=10$. On the other hand, when the size of offline agents is smaller, the offline agents will have fewer communications to form more opinion clusters. Furthermore, low confidence levels clearly enhance these effects.

**Figure 3**. the average *S_NC* values under different T and p values from 1000 independent realizations, where T∈[1,100].

The number of pure opinion clusters

A pure offline cluster can be observed easily. For a fixed $\epsilon\leq 0.13$, the number of pure offline clusters increases from $T=1$ to $T=10$ (observe more details in Figure 5) and nearly stops increasing when the degree of asynchronization exceeds 20 as per Figure 4. The number of pure offline clusters increases from $T=1$ to $T=10$ because of fewer communications between online and offline agents. However, as $T$ increases above this threshold, it is observed that the online agents rapidly reach a steady-state among them, which stops the increase in the number of pure offline clusters. When $\epsilon>0.13$, we barely observe pure offline clusters except a small area in the upper right-hand corner of the third subfigure of Figure 4.

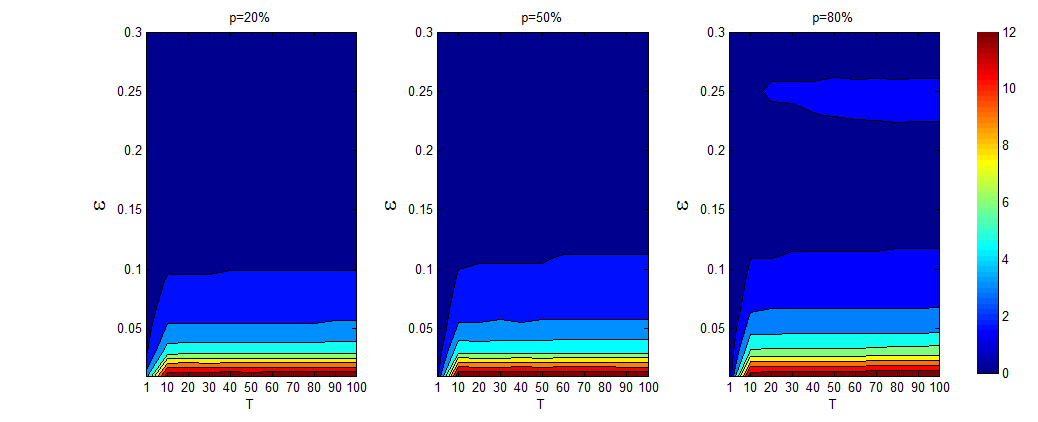
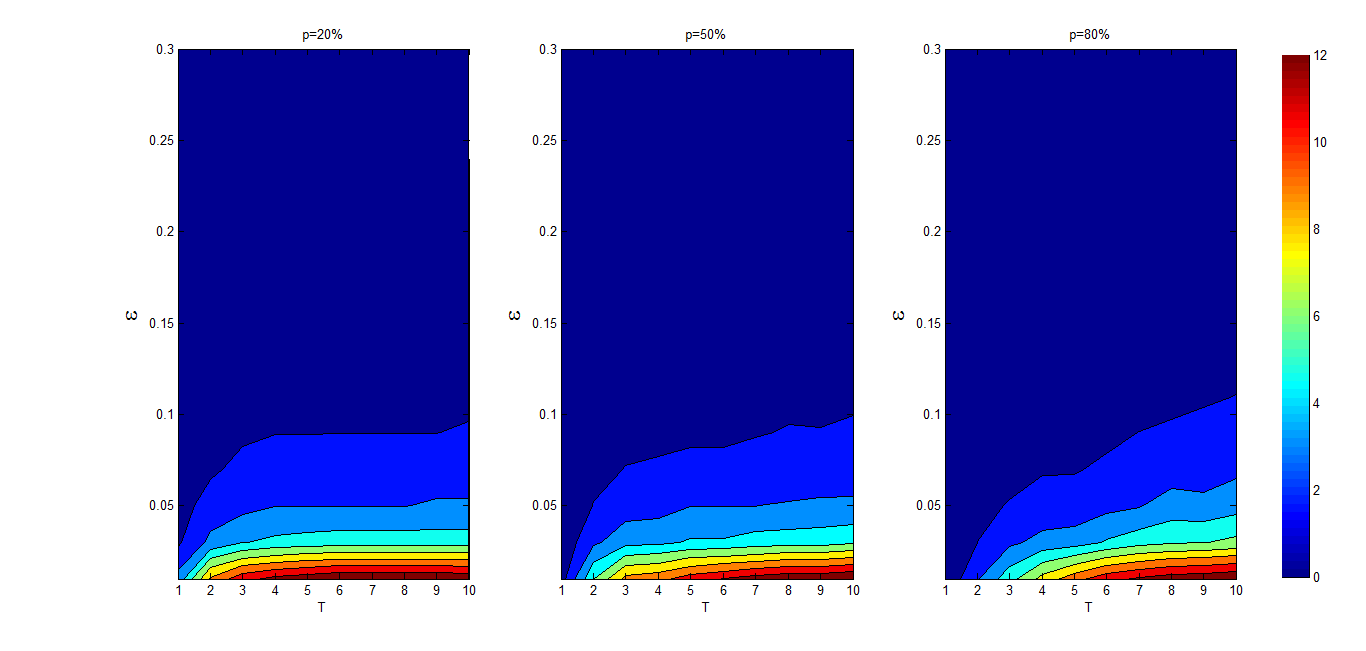
**Figure 4**. The average *S^off_NPC* values under different T and ε values from 1000 independent realizations, where T∈[1,100].

**Figure 5**. The average *S^off_NPC* values under different T and ε values from 1000 independent realizations, where T∈[1,10].

Figure 6 further helps understanding the impact of the size of online agents on the number of pure offline clusters. Indeed, Figure 6 shows that a large size of online agents leads to a large number of pure offline clusters, and such an effect is more evident for $T≥10$ as explained above. Furthermore, low confidence levels clearly enhance these effects.

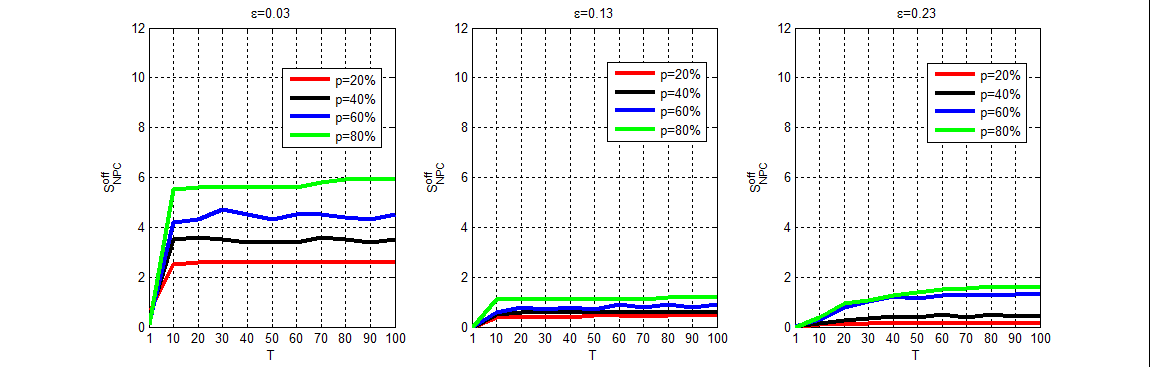
**Figure 6**. The average *S^off_NPC* values under different T and p values from 1000 independent realizations, where T∈[1,100].

However, we find that pure online clusters are hardly observed in the simulation, and this phenomenon implies that online clusters can always attract a certain number of offline agents. Next, we investigate the absorption of the online and offline subsystems to further study the interactions between them.

The absorptions of the online and offline subsystem

Assume that there are $z$ opinion clusters in the stable state, denoted as $c_1,c_2,\dots,c_z$. Let $l_i^{on}$ and $l_i^{off}$ denote the number of online agents and the number of offline agents in opinion cluster $c_i$, respectively. If $l_i^{on}>l_i^{off}$ then $c_i$ is referred to as an online opinion cluster, while if $l_i^{on}<l_i^{off}$ then $c_i$ is referred to as an offline opinion cluster.

In the following, we define $L^{on}$ and $L^{off}$ to measure the absorption of the online subsystem and the offline subsystem, respectively.

$$L^{on}=\frac{\sum_{i=1}^z l_i^{off} \Xi(l_i^{on}-l_i^{off})}{N(1-p)}\text{,}$$

(11)

$$L^{off}=\frac{\sum_{i=1}^z l_i^{on} \Xi(l_i^{off}-l_i^{on})}{Np}\text{,}$$

(12)

Where $\begin{cases}\Xi(x)=1,x>0\\ \Xi(x)=0,x\leq 0 \end{cases}$ and $z$=2. When $z$=1, i.e., all agents reach a consensus, $L^{on}$ and $L^{off}$ are both set by 0.5. Clearly it is $L^{on},L^{off}\in [0,1]$. $L^{off}$ measures the ratio of the offline agents that are absorbed in online opinion clusters, while $L^on$ measures the ratio of the online agents that are absorbed in offline opinion clusters. The larger the value of $L^{on}$ ($L^{off}$), the stronger the absorption of the online subsystem (the offline subsystem).

Figures 7 and 8 illustrate how the absorption of the online subsystem and the absorption of the offline subsystem change along with size of online subsystem and the degree of asynchronization, respectively. When the size of the online subsystem increases, the absorption of the online subsystem becomes strong, while the absorption of the offline subsystem becomes weak. Meanwhile, the impact of $T$ on $L^{on}$ and $L^{off}$ depend on $p$ and $\epsilon$. For low confidence levels (e.g., $\epsilon>=0.03,0.13$), when $T$ increases, $L^{on}$ increases and $L^{off}$ decreases for $p<0.5$, while their direction reverse for $p>0.5$. However, such an effect is not evident for large confidence levels (e.g., $\epsilon=0.23$) due to the numerous communications among agents that are generated in these cases.

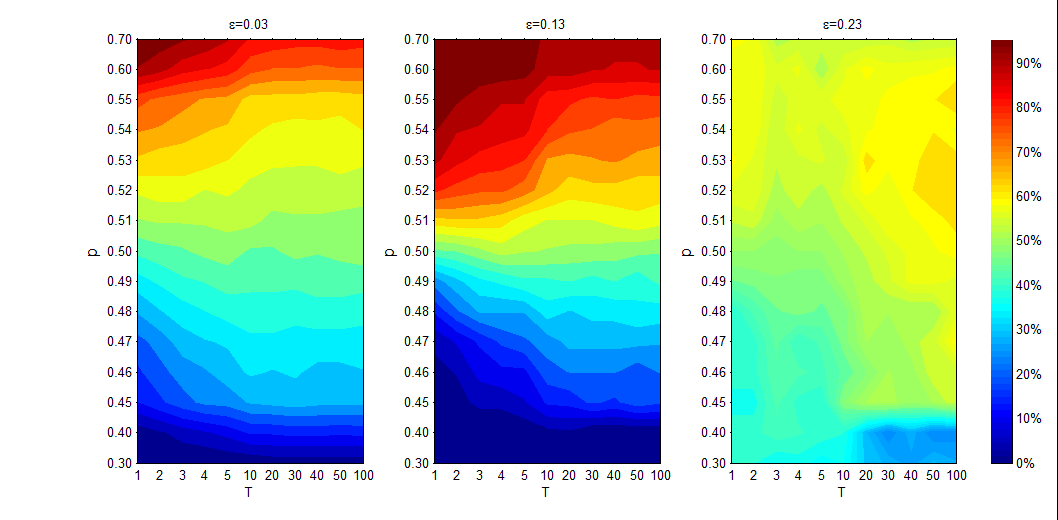
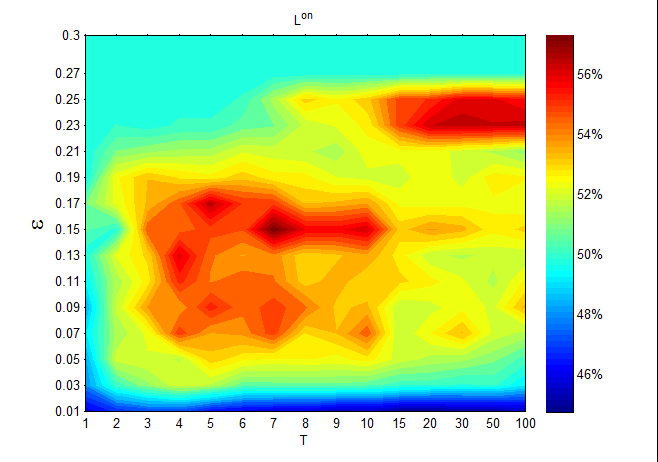
**Figure 7**. The average value of *L^on* under different T, p and ε values from 1000 independent realizations, where T∈[1,100].

**Figure 8**. The average value of *L^off* under different T, p and ε values from 1000 independent realizations, where T∈[1,100].

According to eMarketer Report (2016), in the world about half of the population are online agents, consequently we pay more attention on the case of $p=0.5$ in the following Figures 9-11. $L^{on}$ highlights the centre area of Figure 9. This observation can be explained as follows. When $T$ is small, it is difficult for the online agents to form some online opinion clusters; when $T$ is large, the online agents will rapidly reach a stable state and thus the number of offline agents that are influenced by the online agents will decrease accordingly. Meanwhile, if the confidence level $\epsilon$ is small, the online agents only communicate with a very limited number of the offline agents, and if the confidence level is large, the offline agents can simultaneously attract strongly the online agents. So, when $\epsilon$ and $T$ are both in the middle size, the online subsystem shows a stronger absorption capacity.

Meanwhile, $L^{on}$ highlights the upper right-hand corner of Figure 9. This observation can be explained as follows. When the confidence level is large ($\epsilon=0.23$) and $T$ is small ($T≤10$), all agents can always reach a consensus, and thus $L^{on}$ is 0.5. However, with further increments of $T$, we find that all agents will be gradually divided into two opinion clusters: one is an online opinion cluster and the other one is an offline opinion cluster, with the number of offline agents in the online opinion cluster being high. So, the online subsystem shows a stronger absorption capacity on the upper right corner of Figures 9.

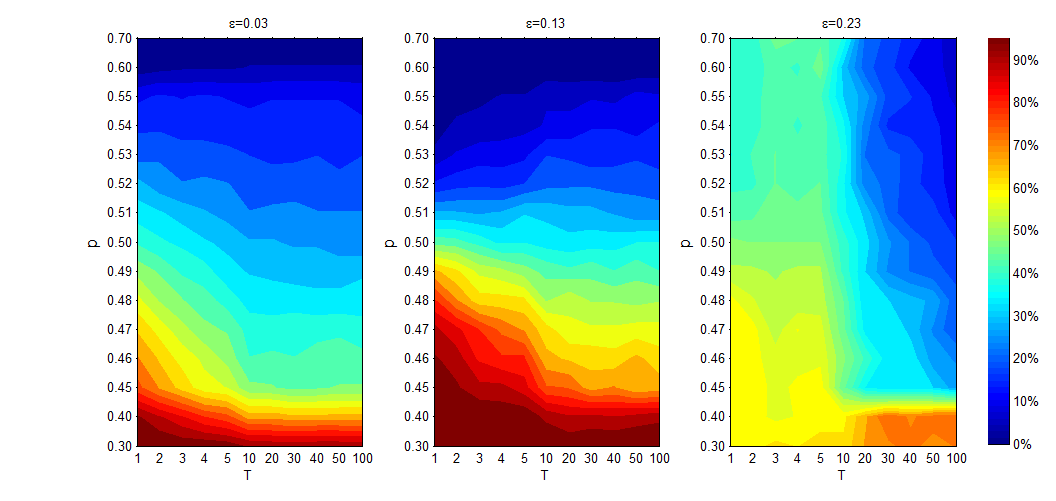
**Figure 9**. The average *L^on* values under different T and ε values from 1000 independent realizations, where T∈[1,100].

Figures 10 shows that $L^{off}$ starts decreasing, and then stabilizes as $T$ increases. The main reason for this observation is that the interaction between the two subsystems decreases as $T$ increases, which leads to a decrease of $L^{off}$. With further increments of $T$, the online agents will reach a stable state before the offline agents start to update opinions. Thus, the interaction between the two subsystems barely changes, and then $L^{off}$ stabilizes.

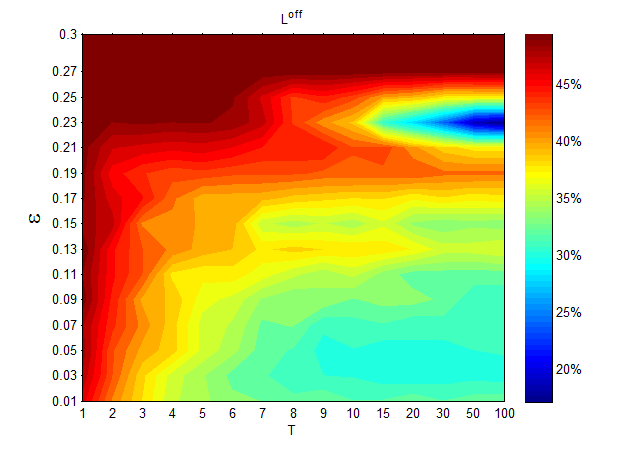
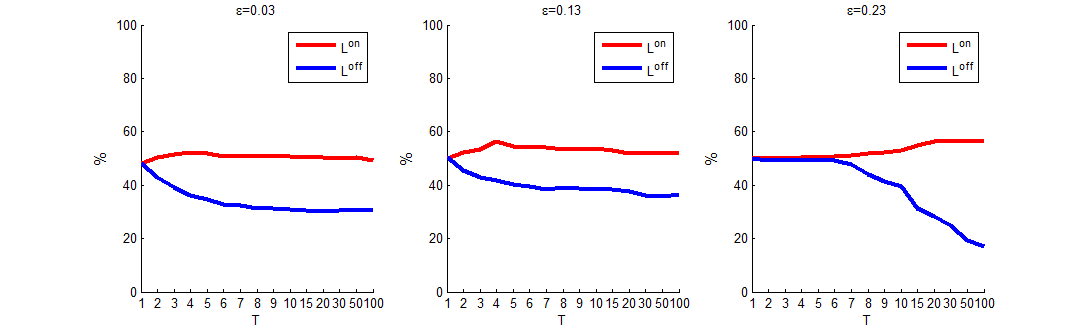
**Figure 10**. The average *L^off* values under different T and ε values from 1000 independent realizations, where T∈[1,100].

On the one hand, as per Figures 9 and 10, the online subsystem has a stronger absorption capacity than the offline subsystem; the online subsystem absorbs approximately 40% ~ 60% of the offline agents, while the offline subsystem absorbs approximately 15% ~ 50% of the online agents. On the other hand, as per Figure 11, the value of $L^{on}$ is always larger than the value of $L^{off}$ for different given confidence levels.

**Figure 11**. The average *L^on* values vs. the average *L^off* values from 1000 independent realizations, where T∈[1,100].

Conclusions

In this paper, we propose asynchronous opinion dynamics with online and offline interactions in a bounded confidence model. In the proposed model, the asynchronous updating mechanisms between the online and offline agents are analyzed in detail.

We unfold that the asynchronization strongly impacts the steady-state time, the number of opinion clusters and the interaction between the online and offline agents, and that as the size of the online agent increases these effects are enhanced.

We show that online agents have a stronger absorption capacity than offline agents, which leads to the appearance of pure offline clusters. Thus, we suggest that governments should provide more supports to promote interactions with some offline agents; otherwise, some of the offline agents could end up being isolated from society.

With the development of Information and Internet technology, asynchronization between online and offline agents is a very popular phenomenon in the evolution of real-life public opinions. In order to make our research more realistic and reliable, we plan to develop further studies to improve the understanding of asynchronization in opinion dynamics in other relevant models, and to extend the study in a complex network context.

Acknowledgements

We would like to acknowledge the financial support of grants (Nos. 71571124 and 71601133) from NSF of China.

Appendix

A. The steady-state time

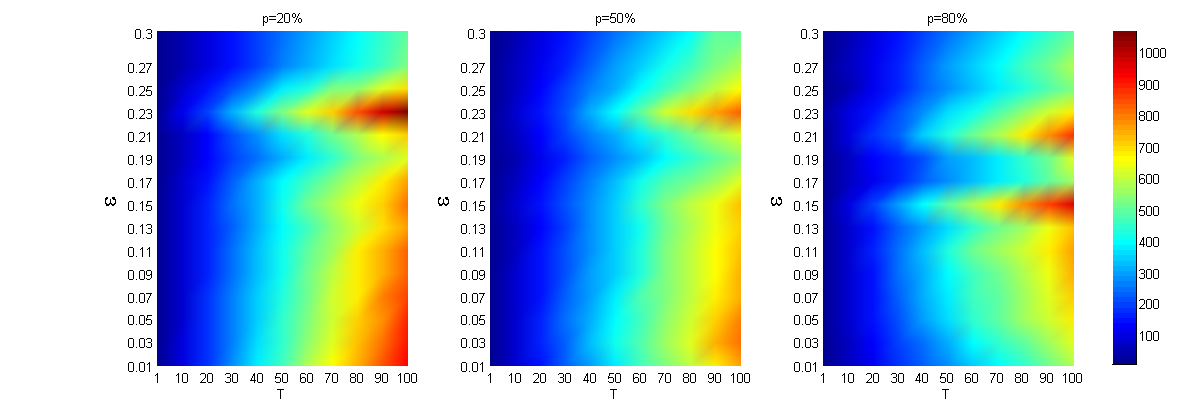
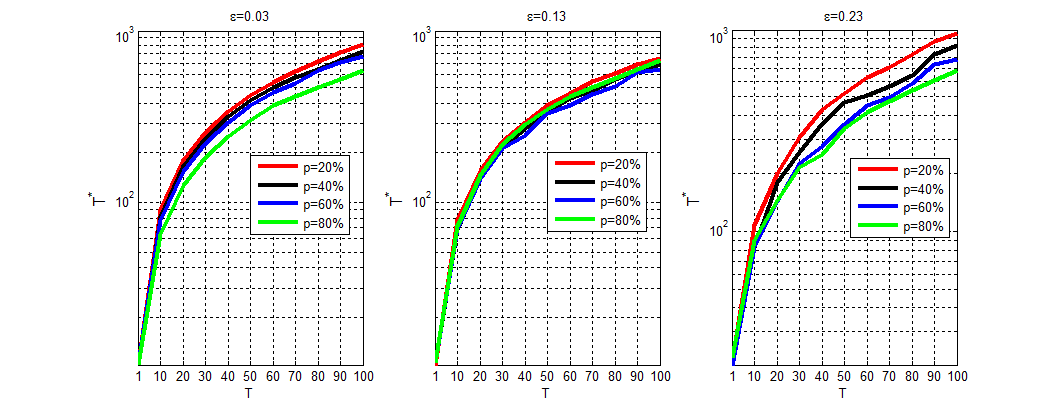
Figure 12 reveals the impact of $T$ and $\epsilon$ on the steady-state time $T^*$. As $T$ increases, the steady-state time $T^*$ increases under the different $\epsilon$ values. Compared with synchronization (i.e. $T=1$), the offline agents update their opinions more slowly than the online agents, and thus the evolution of opinions needs a longer time to reach a stable state. Particularly, the difference of the steady-state time between the synchronization case and the asynchronization case with large $T$ is very obvious.

A clue can be found in Figure 12 showing the relationship between the size of the online subsystem and the steady-state time: The smaller the online subsystem is, i.e. the smaller $p$ is, the longer it took in time for the stabilization of opinions when $\epsilon\leq 0.11$. However, this observation cannot always be obtained when $\epsilon>0.11$. We can clearly see this thread from Figure 13: When the value of $\epsilon$ is small $\epsilon=0.33$, the steady-state time decreases when the size of the online subsystem increases, while the result does not hold when $\epsilon=0.13$. As shown in the middle subgraphs of Figure 13, it took more time for the stabilization of opinions when $p$=80% than for $p$=60%.

The main reason for this observation is that the steady-state time $T^*$ is simultaneously affected by $p$ and $\epsilon$. When $\epsilon$ is small $\epsilon\leq 0.11$, the steady-state time $T^*$ is mainly affected by $p$, and we find that there is the above regularity between the size of the online subsystem $p$ and the steady-state time $T^*$. However, as the value of $\epsilon$ increases, the influence of $\epsilon$ on the steady-state time $T$* grows, which leads that there is not an obvious regularity between $p$ and $T^*$.

**Figure 12**. The average T* values under different T and ε values from 1000 independent realizations, where T∈[1,100].

**Figure 13**. The average T* values different T and p values from 1000 independent realizations, where T∈[1,100].

B. The pseudo-code of calculating opinion clusters

References

ALIZADEH, M., & Cioffi-Revilla, C. (2015). Activation regimes in opinion dynamics: comparing asynchronous updating schemes. Journal of Artificial Societies and Social Simulation, 18(3), 8: https://www.jasss.org/18/3/8.html. [doi:10.18564/jasss.2733]

BAKSHY, E., Rosenn, I., Marlow, C., & Adamic , L. (2012). The role of social networks in information diffusion. Proceedings of the 21st international conference on World Wide Web. ACM, 519-528.

BERGER, R.L. (1981). A necessary and sufficient condition for reaching a consensus using Degroot’s method. Journal of the American Statistical Association, 76, 415-418. [doi:10.1080/01621459.1981.10477662]

BERTSEKAS, D. P., & Tsitsiklis, J. N. (1989). Parallel and distributed computation: numerical methods. Englewood Cliffs, NJ: Prentice hall.

CERAGIOLI, F., & Frasca, P. (2012). Continuous and discontinuous opinion dynamics with bounded confidence. Nonlinear Analysis: Real World Applications, 13(3), 1239–1251. [doi:10.1016/j.nonrwa.2011.10.002]

CHEN X., Zhang H.J., & Dong Y.C. (2015). The fusion process with heterogeneous preference structures in group decision making: A survey. Information Fusion, 24,72-83.

DEFFUANT, G., Neau, D., Amblard, F., & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems 3(01n04), 87-98. [doi:10.1142/S0219525900000078]

DEGROOT, M.H. (1974). Reaching a consensus. Journal of the American Statistical Association, 69, 118-121.

DONG, Y.C., Chen, X., Liang, H.M., & Li, C.C. (2016). Dynamics of linguistic opinions formation in bounded confidence model. Information Fusion 32, 52-61. [doi:10.1016/j.inffus.2016.03.001]

DONG, Y.C., & Zhang,H.J. (2014). Multiperson decision making with different preference representation structures: A direct consensus framework and its properties. Knowledge-based Systems, 58, 45-57.

FORTUNATO, S., Latora, V., Pluchino, A., & Rapisarda, A. (2005). Vector opinion dynamics in a bounded confidence consensus model. International Journal of Modern Physics C, 16(10), 1535-1551. [doi:10.1142/S0129183105008126]

FRENCH, J.R.P. (1956). A formal theory of social power. Psychological Review, 63, 181-194.

FRIEDKIN, N.E., & Johnsen, E.C. (1990). Social influence and opinions.Journal of Mathematical Sociology, 15, 193-205. [doi:10.1080/0022250X.1990.9990069]

FROMMER, A., & Szyld, D. B. (2000). On asynchronous iterations. Journal of Computational and Applied Mathematics, 123, 201-216.

HEGSELMANN, R., & Krause, U. (2002). Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2: https://www.jasss.org/5/3/2.html.

KOZYAKIN, V. S. (2003). Asynchronous systems: a short survey and problems. Preprint, 1-19.

LIANG, H.M., Dong, Y.C., & Li, C.C. (2016). Dynamics of uncertain opinion formation: An agent-based simulation. Journal of Artificial Societies and Social Simulation, 19(4), 1: https://www.jasss.org/9/4/1.html. [doi:10.18564/jasss.3111]

LORENZ, J. (2006). Consensus strikes back in the Hegselmann-Krause model of continuous opinion dynamics under bounded confidence. Journal of Artificial Societies and Social Simulation, 9(1), 8: https://www.jasss.org/9/1/8.html.

MATHIAS, J.D., Huet, S., & Deffuant, G. (2016). Bounded Confidence Model with Fixed Uncertainties and Extremists: The Opinions Can Keep Fluctuating Indefinitely. Journal of Artificial Societies and Social Simulation, 19(1), 6: https://www.jasss.org/19/1/6.html. [doi:10.18564/jasss.2967]

MORARESCU, I. C., & Girard, A. (2011). Opinion dynamics with decaying confidence: Application to community detection in graphs.IEEE Transactions on Automatic Control, 56(8), 1862–1873.

SONG, X.L., & Yan, X.B. (2012). Influencing factors of emergency information spreading in online social networks: A simulation approach.Journal of Homeland Security and Emergency Management, 9(1), 183b. [doi:10.1515/1547-7355.1979]

URBIG, D., Lorenz, J., & Herzberg, H. (2008). Opinion dynamics: The effect of the number of peers met at once. Journal of Artificial Societies and Social Simulation, 11(2), 4: https://www.jasss.org/11/2/4.html.

WEISBUCH, G. (2004). Bounded confidence and social networks. The European Physical Journal B(E.P.J.B)-Condensed Matter and Complex Systems, 38, 339-343. [doi:10.1140/epjb/e2004-00126-9]

WORLDWIDE Internet and Mobile Users: eMarketer's Updated Estimates and Forecast for 2015–2020 (eMarketer Report). Published October 11, 2016: https://www.emarketer.com/Report/Worldwide-Internet-Mobile-Users-eMarketers-Updated-Estimates-Forecast-20152020/2001897.

ZHAO, W. X., Jiang, J., Weng, J. S., He, J., Lim, E. P., Yan, H.F., & Li, X.M. (2011). Comparing twitter and traditional media using topic models. European Conference on Information Retrieval. Springer Berlin Heidelberg.