An Agent-Based Model of Motor Insurance Customer Behaviour in the UK with Word of Mouth

,
and
Bayes Business School, City, University of London, United Kingdom
Journal of Artificial
Societies and Social Simulation 25 (2) 2
<https://www.jasss.org/25/2/2.html>
DOI: 10.18564/jasss.4768
Received: 26-Aug-2021 Accepted: 24-Jan-2022 Published: 31-Mar-2022
Abstract
Attracting and retaining loyal customers is a key driver of insurance profit. An important factor is the customers' opinion of an insurer's service quality. If a customer has a bad experience with an insurer, they will be less likely to buy from them again. Word-of-mouth networks allow information to spread between customers. In this paper we build an agent-based model with two types of agents: customers and insurers. Insurers are price-takers who choose how much to spend on their service quality, and customers evaluate insurers based on premium, brand preference, and their perceived service quality. Customers are also connected in a small-world network and may share their opinions with their network. We find that the existence of the network acts as a persistent memory, causing a systemic bias whereby an insurer's early reputation achieved by random chance tends to persist and leads to unequal market shares. This occurs even when the transmission of information is very low. This suggests that newer insurers might benefit more from a higher service quality as they build their reputation. Insurers with a higher service quality earn more profit, even when the customer preference for better service quality is small. The UK regulator is intending to ban the practice of charging new customers less than renewing customers. When the model is run with this scenario, the retention rates increase substantially and there is less movement away from insurers with a good initial reputation. This increases the skewness in market concentrations, but there is a greater incentive for good service quality.Introduction
Insurance is a service whereby providers offer compensation payouts if the customer suffers a loss due to a specified type of event. In many countries, some types of insurance are mandatory: for example, all motorists in the UK must have motor insurance against legal responsibility for damage to another motorist’s person or property. Insurance is a substantial part of the financial services industry and an important part of social fabric.
It is common for general (i.e., non-life) insurance contracts to cover a fixed term, usually one year. At the end of the term, customers receive a renewal offer from their current insurance providers. Since searching for new quotes costs both time and effort, many customers choose to accept their renewal price without searching. UK motor insurance customers consider the cost of searching for a new insurer to be worth \(15\%\) of the average cost of their policy (FCA 2020). It costs insurers less to retain an existing customer than to attract and process a new one, and insurance is a highly competitive industry. Attracting and then retaining loyal customers is therefore often a better strategy than competing on price alone. It is common practice for insurers to offer a discount for new customers, often pricing below the odds, then rely on loyalty and gradually increase the price. In essence, loyal customers are used to cross-subsidize new customers (FCA 2020).
The probability of renewal is commonly modelled as a logit relationship, and existing literature has employed various techniques to identify which customers are likely to be loyal. Smith et al. (2000) compares the performance of logistic regression, decision trees, and a neural net in classifying and predicting the loyalty of motor insurance customers. Günther et al. (2014) builds on the logit regression model, using generalised additive models to allow for non-linear relationships. Zhang et al. (2017) combines a neural net with a generalised linear model to take advantages of the strengths of both approaches.
Customer service is considered an important factor in customer retention in many industries, and this link has been confirmed in a number of empirical case studies in insurance (Ansari & Riasi 2016; Ghodrati & Taghizad 2014; Tsoukatos & Rand 2006). These papers indicate that though price remains the main factor in customer choice, customer service is a significant part of customer decision making. Customers are also highly influenced by word-of-mouth recommendations from friends (Ghodrati & Taghizad 2014; Tsoukatos & Rand 2006). Berger (1988) investigates this using a model where insurance customers remain with a firm unless they have a bad experience, which happens infrequently as claims are also infrequent. When they decide to switch, they choose a new insurer when a friend makes a recommendation. Interestingly, as the rate of recommendation transmissions is increased, the number of dissatisfied customers decreases but the average quality decreases. This is because a higher number of dissatisfied customers switch providers, including to lower quality firms. Because customers usually do not have a customer experience, the low quality is not often discovered, and so many of these customers felt satisfied. However, this paper does not include an allowance for pricing considerations or other customer preferences, and does not model the network explicitly.
Berger et al. (1989) bases customer decisions on price as well as service. In this model, customers have imperfect information and only gradually discover the available prices through word-of-mouth. Customers favour renewals unless they believe there is a sufficiently big price differential, and disatisfied customers requires a lower price gain to be willing to switch. By fitting this model to real-world data, the authors estimate that customers have a high speed of information transmission, but a high reluctance to switch. This paper does not explicitly model the network, choosing instead to use a formula for the rate of information spread. Since this paper was written, it has become easier for customers to get hold of information, and for social networks to allow the transmission of word-of-mouth information.
Conventional analytical approaches may be insufficient to capture network effects, as some features are emergent properties of non-linear interactions. Agent-based models (ABMs) have been used within sociology to model the spread of market innovations and social opinions (Bianchi & Squazzoni 2015; Squazzoni 2012). Kowalska-Styczeń & Sznajd-Weron (2016) use an ABM to examine the effect of different word-of-mouth patterns on the resulting market shares. Goldenberg et al. (2001) used a celluar approach to simulate ‘strong’ ties within a group and ‘weak’ ties between cells, finding that though strong ties have higher influence within groups, weak ties are as important as strong as they are responsible for new word-of-mouth information into the groups.
The general insurance market features interacting heterogeneous agents making decisions over time to maximise some reward function based on past experience. This would seem to be a promising fit for an agent-based modelling approach (Mills 2010; Palin et al. 2008; Parodi 2012). There are currently very few examples of ABM literature in the field of insurance, though the possibilities of ABMs have attracted the interest of several actuarial practitioners.
Crabb & Shapiro (1996) builds a simulation game with the aim of educating students by allowing them to set the strategy of a motor insurance company and compete against other agents. Insurance World 2 (Gionta 2000) is a simulation built by the AI analysis company Complexica for a consortium of insurance and reinsurance companies to examine the consequences of different strategies in a catastrophe reinsurance market. Alkemper & Mango (2005) build an ABM of a property-casualty reinsurance market where capital requirements act as a capacity constraint on supply and the price is then calculated from a demand-supply curve. This simple setup produces price cycles from the competitive interactions. However, it is not possible to obtain a detailed description of these models and their parameterisation.
Dubbelboer et al. (2017) implements an ABM focussed on flood risk management with an insurance component. This model is used to explore scenarios of public and private flood risk cover within a London borough and the subsequent effect on homeowners. This paper focuses mainly on the housing market, including homeowner and developer agents, and a government flood reinsurance. There is no insurance market or competitive aspect to the insurance, which is provided by a single insurer agent which prices its business purely on the level of risk.
Owadally et al. (2018) uses an ABM of an insurance market to investigate possible mechanisms for the cyclical behaviour exhibited by real-world insurance premiums. This model contains two types of agents: insurers and customers. Insurers adjust their initial risk-based premium according to an estimation of the current elasticity of demand. Customers select their preferred insurers based on a combination of the cost and their own preference for particular brand or product features. This ABM was found to produce cycles similar to those seen in the real-world as an endogenous feature of the competitive mechanism. Owadally et al. (2019) further extends this model with a framework aimed at assisting regulators in monitoring and responding to cycles by running simulations of various regulation and brand strategy scenarios parameterised with the current market position and introducing extensive time-series analysis of the outputs. These models are mainly concerned with the premium behaviour of insurers, and do not explore the impact of insurer quality or the network effects of social influence on customer decisions. However, these papers are notable in the field of insurance ABMs for introducing a simple yet credible model of both consumer and insurer behaviour within a competitive system, and producing outputs which are validated against historical real-world market level premium and loss data.
Heinrich et al. (2021) use ABMs to investigate systemic risk within catastrophe insurance and reinsurance markets. The overwhelming majority of insurers within these markets purchase data about the estimated risk of these events from the same same three providers. This paper simulates a catastrophe insurance and reinsurance market and examines the effects of different scenarios of varying diversity of information where the available catastrophe models each underestimate a particular type of loss. They find that lower model diversity increases the rate of bankruptcies and decreases the overall levels of market capital, implying a possible source of systemic risk within the real-world catastrophe insurance markets.
The examples mentioned so far are focussed on the insurers or regulation rather than on customer renewal and insurer selection. Boucek & Conway (2003) suggests a model where customers will renew with an insurer if their new premium has decreased or increased by only a small amount, and become more likely to seek further quotes the more their premium has increased. Customers are heterogeneous and possess various factors which insurers might use to assess their risk; e.g. age, gender, level of education. This model does not include other factors such as satisfaction with service, though the author does note its potential importance. The paper also mentioned the need for industry data and does not parameterise the model, though it does demonstrate some example scenarios. Ulbinaite & Le Moullec (2010) proposed a similar ABM for life insurance customer behaviour, though again this model is described in theory but neither parameterised nor implemented. In this paper, purchase decision is two stage: firstly, the customer decides whether to purchase insurance at all, based on a linear combination of various factors which influence their perception of the value of the insurance versus its affordability. In the second stage, customers decide which insurer to purchase from based on their opinion of the quality of the insurer. Though this paper includes interaction with social networks as a factor in customer decision, it does not specify how this interaction would be calculated or how such a network would be modelled.
In this paper, we will use an ABM to simulate a word-of-mouth network within an insurance network where customer choices are influenced by their opinion of customer service quality, and parameterise the model with data from the UK motor insurance market. We will use this model to examine some of the systemic effects of the network on patterns of customer behaviour, and investigate possible implications of a proposed change in UK insurance regulation. By modelling the network explicitly, we can explore the impact of realistic network dynamics and in particular the repeated feedback of word-of-mouth information back into the network. This allows us to explore systemic effects not captured in early models such as those of Berger (1988) or Berger et al. (1989).
We find that the existence of the network acts as a persistent memory, causing a systemic bias whereby an insurer’s early reputation achieved by random chance tends to persist and leads to market concentration with a few insurers holding large market shares. We demonstrate that it only takes a very low rate of word-of-mouth transmission for this effect to significantly impact market-wide customer decision-making. In a market where insurers are of varying quality, we discover that higher quality insurers make a higher profit despite offering higher prices. This occurs when customers have only a weak preference for better service quality. Finally, we explore the impact of a new regulation change and discover that this may lead to lower competition and an increasingly skewed market concentration, but potentially also incentivise higher service quality.
Based on these findings, we can conclude that the potential impact of the word-of-mouth network on customer decision-making and the resulting systemic biases is a significant one. These findings should be considered by both insurers considering strategies for attracting and retaining customers, and regulators who are assessing possible impacts of a change in the regulation of insurance pricing practices.
Model
Overview
The aim of this model is to explore patterns of insurance customer choices arising from the existence of a word-of-mouth mechanism. As such, the design focuses on features observed by the customers. The model therefore does not attempt to replicate the internal workings or processes affecting the strategic decision-making processes of the insurance companies such as reinsurance or credit risk. We also assume that there is no claims fraud and that policies have similar cover such that all insurers will sample from the same claims distribution.
The ABM contains two types of agents: insurers and customers. These act within the environment of a motor insurance market. At each simulation, the model undergoes the following steps:
- Network generation: At the start of the simulation, the model generates a small world network of social links between the customers, and randomly assigns each customer to an initial insurer (2.30).
- Insurer spending: Insurers choose how much to spend per customer on their level of customer service up to some maximum level (2.16). The more they spend, the greater the chance that any given customer interaction will be a positive and not a negative experience for the customer (2.21).
- Insurer premium: As this model does not focus on insurer premium strategy, the market premium is set exogenously and follows a simple cyclical pattern similar to those found in existing research (Fenn & Vencappa 2005) fitted to empirical data, with a stochastic error term (2.9). Insurers will also add a margin to cover their spending cost and profit markup (2.17). Prices for new customers are discounted relative to prices for renewing customers (2.19).
- Customer purchases: Customers decide whether to renew based on a logit probability function (Günther et al. 2014) based on the change in cost over the previous year (2.36). This is parameterised to give an average chance of renewal that matches empirical data. If they do not renew, they will purchase from the insurer that offers them the lowest total cost (2.37).
- Claims: Loss events - e.g. theft or traffic accidents - are modelled probabilistically using a Poisson frequency and Gamma severity (2.39). If a customer experiences a loss, they make an insurance claim. Their interaction with their insurer’s customer service which may generate a good or bad experience with probability based on the amount spent on customer service. (2.21)
- Customer word-of-mouth information sharing: Customer service experiences tend to perpetuate across networks as customers tell their friends of their experiences or experiences they’ve heard about (2.42). The influence of these opinions is calculated using a method similar to many opinion dynamic models (Deffuant et al. 2002) ( 2.46 - 2.52).
- Customer cost calculations: The customers re-assess insurers based on a cost function. Similar to Owadally et al. (2018), this is not just based on pure price. There is an allowance for preferences, and a cost factor based on a customer satisfaction assessment of each insurer (2.33).
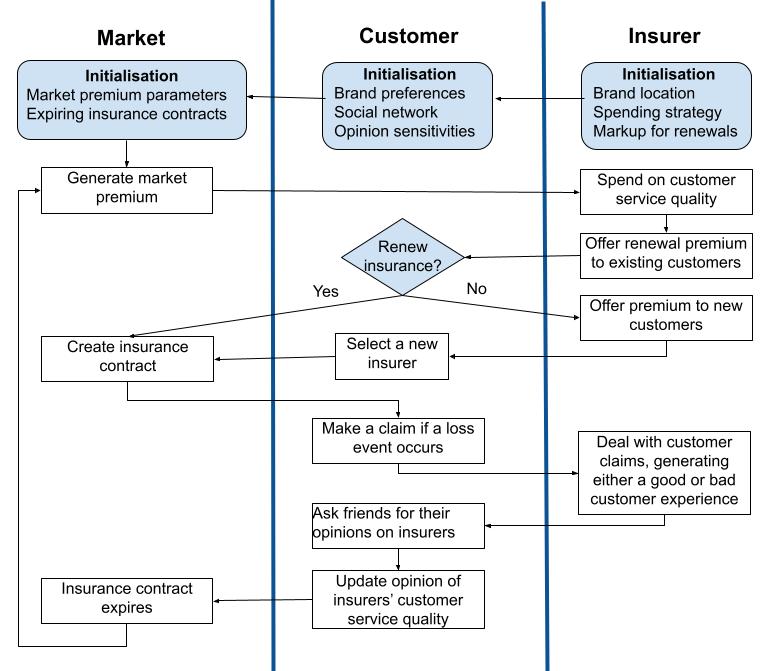
Figure 1 is a swimlane diagram representing the flow of processes in the model and which agent or environment is responsible for each step. The calculations carried out at each step are described in more detail below, followed by an explanation of the data and model parameterisation.
Figure 2 shows the pseudocode for the initialisation at the start of the simulation, and Figure 3 demonstrates the pseudocode for a timestep. The parameter notation has been kept consistent with the model descriptions below. The pseudocode for the functions referenced are shown alongside the relevant sections. Additionally, the code has been made available on CoMSES (England et al. 2021).


Market
Description
In this model, agents interact within the environment of an insurance market. The market contains two types of agents: insurers and customers. Each timestep, all customers will create an insurance contract with one insurer.
The model is based on the UK motor insurance market. In the UK, it is mandatory for all motorists to purchase motor insurance, so demand is stable. It is therefore reasonable to assume that all customers will purchase an insurance contract each timestep. There are no exits or entrants in the model.
The expiration of the insurance contracts at the start of each timestep triggers the customer agents to seek premium quotes and select an insurer with which to form a new contract. The premium quotes are described further in paragraphs 2.17 and 2.19, and the customers’ insurer selection process in paragraphs 2.33 to 2.37.
As this model does not focus on premium behaviour, the model does not attempt to replicate the individual insurer strategy that would produce the patterns seen in competitive premium rates. Instead, the market premium is assumed to follow an exogenous stochastic process. The insurers are assumed to be price takers, and they use the market premium as a basis for selecting their own premium to offer to existing and new customers.
Inputs and Initialisation
- \(n_C\): The number of customer agents seeking to purchase insurance.
- \(n_I\): The number of insurer agents operating in the marketplace.
- \(\overline{P}_{-1}\): The market premium (price per customer) in the year prior to the first time step.
- \(\overline{P}_{-2}\): The market premium in the year two years prior to the first time step.
- \(\theta_{0}\): The constant term in the market premium calculation.
- \(\theta_{1}\): The dependency of the current market premium on the previous year’s market premium.
- \(\theta_{2}\): The dependency of the current market premium on the market premium two years previously.
- \(\sigma_{M}\): The stochastic variance of the market premium around its expected value.
Calculations
Setting the market premium rate. It is common to model insurance market premium as an AR(2) process (Boyer & Owadally 2015; Cummins & Outreville 1987; Fenn & Vencappa 2005; Harrington & Niehaus 2000; Owadally et al. 2019, 2018). Using this formulation, the market insurance price per customer \(\overline{P}_{t}\) for timestep \(t\) is calculated exogenously according to Equation 1 below.
| \[ \begin{split} & \overline{P}_{t}=\theta_{0}+\theta_{1}\overline{P}_{t-1}+\theta_{2}\overline{P}_{t-2}+\epsilon_{t} \\ & \mbox{where } \epsilon_{t}\sim N\left(0,\sigma_{M} \right) \end{split}\] | \[(1)\] |
Outputs
- \(\overline{P}_{t}\): The (exogeneous) market premium in timestep \(t\), calculated according to Equation 1.
- \(\overline{\Pi}_{t}\): The market profit in timestep \(t\). This is the sum of the profits made by the insurer agents in time \(t\).
- \(\overline{R}_{t}\): The market renewal rate in timestep \(t\). This is calculated as the proportion of customers in time \(t\) who choose to renew their insurance contract with their existing insurer.
Insurers
Description
The insurer agents provide motor insurance cover for loss events experienced by their customers, such as theft or damage caused by a car accident. As their aim is to make a profit, insurers will usually charge customers more than the expected value of their losses. Because they have pooled the risks from many customers, the relative volatility of an insurer’s total loss is less than that of an individual customer.
Insurers are modelled as price takers, setting their premium according to the prevailing market premium. They also charge a margin for their expenses, and an additional margin for profit. To entice new customers, insurers remove the extra profit margin for new quotes, effectively using the renewals of existing customers to subsidise new customers.
When a customer makes a claim, they interact with the insurer’s customer service department. This interaction can be either a good or bad experience for the customer, and this outcome will directly alter the customer’s opinion of the insurer. The more money the insurer has chosen to spend on their customer service quality, the higher the probability that this interaction will be a positive experience for the customer.
Inputs and Initialisations
The insurer agents are indexed by \(i\).
- \(E\): The maximum effective insurer spend per customer on customer service quality.
- \(E_{i}\): The amount spent by insurer \(i\) per customer on customer service quality at the start of each timestep.
- \(R\): The profit markup factor applied to existing customers renewing their insurance contracts.
- \(T\): The maximum time over which the renewing markup factor applied to existing customers is increased.
Similarly to Owadally et al. (2018), the insurers are also spaced out evenly across a 1-dimensional abstract preference space in a random order. This represents differences in branding or product design features. As in the Owadally et al. (2018) model, this space is circular so that the value bounds have zero distance between them. The location on this space is valued between \([0,2)\). This has been scaled so that the distance between any two points must lie within \(\left[0,1\right]\). The location assigned to an insurer \(i\) is denoted \(L_{I,i}\).
Insurer \(i\) spends an amount \(E_{i}\) on customer service quality per customer at the start of each timestep \(t\). The higher this spend, the better the quality of customer service. It is assumed that there is an upper bound past which extra spending will have little effect on the outcome of customer service interactions; this is the maximum spend \(E\).
In the real world, insurers might choose to vary this spend, though we might expect that a particular brand would not generally wish to vary this by a large amount every year. In this ABM, the focus is on customer behaviour rather than insurer strategy, so each insurer \(i\) is assigned a single value which they spend every year.
Calculations
Setting the price of insurance for new customers.Insurers are modelled as price takers, so they base their premium on the market premium. They also add an expense margin to cover the cost of their customer service expenditure. Thus, the base premium charged to a new customer by insurer \(i\) in time step \(t\) is set according to Equation 2. Consequently insurers trade-off between attracting customers with a lower premium or with a higher service quality.
| \[ P_{it}=\overline{P}_{t}+E_{i}\] | \[(2)\] |
Offering renewal price to existing customers. It is common practice for insurers to entice new customers with a lower initial premium before then increasing the premium gradually on renewal to make a profit (FCA 2020). The FCA report into insurer pricing practices (FCA 2020) shows that most of the increase in prices for renewing customer take place over the first few years.
To mimic this increasing markup, \(P_{ijt}\), the premium offered by insurer \(i\) to an existing customer \(j\) at time step \(t\), is calculated according to Equation 3 where \(T_{ijt}\) is the number of consecutive years that customer \(j\) has been a customer of insurer \(i\) at the start of time \(t\). \(R\) is the renewal markup applied to the base premium cost.
| \[ P_{ijt}={P}_{it}(1+R)^{Min\left(T_{ijt},T\right)}\] | \[(3)\] |
Note that Equation 3 simplifies to Equation 2 for new customers since \(T_{ijt}=0\) for new customers. We can therefore use the signifier \(P_{ijt}\) to indicate the premium offered by insurer \(i\) for both new and renewing customers.
Dealing with customer claims. When a customer experiences a loss, they interact with their insurer’s customer services. The probability \(p_{i}\) of having a good experience will depend on how much the insurer chooses to spend on their customer service, up to the maximum amount. This probability is given by Equation 4.
| \[ p_{i}=\frac{Min\left(E_{i},E\right)}{E}\] | \[(4)\] |
Figure 4 shows the pseudocode for the claims process. Each customer generates a loss frequency and severity from a Poisson-Gamma aggregate distribution. For each claim event, the customer records either a positive or negative outcome from their selected insurer.

Outputs
- \(\Pi_{it}\): The profit made by insurer \(i\) in timestep \(t\). This is equal to the total premium in minus the claims paid out and minus the total expenditure on customer service quality per customer.
- \(R_{it}\): The market renewal rate in time step \(t\). This is calculated as the proportion of existing customers of insurer \(i\) who chose to renew their insurance contract in timestep \(t\).
- \(m_{n,it}\): Number of insurance contracts that insurer \(i\) sold to new customers in timestep \(t\).
- \(m_{s,it}\): Total number of insurance contract sales made by insurer \(i\) in timestep \(t\).
- \(m_{-,it}\): Number of negative customer service experiences experienced by customers of insurer \(i\) in timestep \(t\).
- \(m_{+,it}\): Number of positive customer service encounters experienced by customers of insurer \(i\) in timestep \(t\).
- \(z_{it}\): Average output of customer service encounters experienced by customers of insurers \(i\) in timestep \(t\). Calculated as \(z_{it}=\frac{m_{+,it}-m_{-,it}}{m_{+,it}+m_{-,it}}\) (or set as \(0\) if there were no customer service interactions).
Customers
Description
Customer agents seek to purchase a motor insurance contract from an insurer agent. Each year, they decide whether to renew their existing contract with the same insurer. The greater the increase in the perceived cost of the contract, the lower the probability that they will decide to renew. If they choose not to renew their contract, they seek quotes from all available insurers, and select the provider with the lowest perceived cost.
A customer’s assessment of perceived cost is not just based on premium, but also includes an adjustment for branding and product preferences, and an adjustment for their opinion of an insurer’s customer service quality.
During the ensuing year, a customer might experience event, such as a traffic accident or theft. If this occurs, the customer makes a claim from their insurer by interacting with their customer service. This experience could be a positive or a negative interaction for the customer. Additionally, customers may ask each contact on their social network for their opinion on each insurer. This gossip is interpreted as extra information about customer service quality.
The customers update their opinion on each insurer in light of new information, either from their friends or based on their own experiences, though they give more weight to their own experiences. This will be used as their basis for selecting an insurer in the following year. In turn, they will also use it to spread word-of-mouth information to their friends during the course of the following year. Thus, opinions will spread through friendship groups.
Inputs and Initialisations
The customer agents are indexed by \(j\).
- \(n_{K}\): Average number of links each customer has on their social network.
- \(\beta\): Probability of re-wiring used to construct the social network.
- \(a\): Sensitivity of renewal probability to change in cost.
- \(b\): Baseline renewal probability parameter.
- \(k_{Q}\): Sensitivity of customers’ cost assessment to insurer customer service quality
- \(k_{D}\): Sensitivity of customers’ cost assessment to insurer branding.
- \(\varphi\): Rate at which old information about insurers is forgotten as customers place more emphasis on recent information.
- \(k_{W}\): Influence of social network on customers’ opinion of insurer service quality.
- \(\mu_{f}\): A customer’s average number of claims per year.
- \(\mu_{s}\): Average size of an individual customer claim.
- \(\sigma_{s}\): Standard deviation of the size of an individual customer claim.
- \(p_{W}\): Probability of a customer obtaining word-of-mouth information from a friend who has information about an insurer.
To represent a social network, the Watts-Strogatz algorithm is used to generate a ‘small world’ network between the customers (Watts & Strogatz 1998) at initialisation. This algorithm generates clustered groups with enough links between the clusters to create a small path size, and is commonly used to model real-world social networks. We note that although this algorithm produces the small path size and high level of clustering seen in real-world networks, it does not produce a very varied degree distribution. In real-world social networks, it is common for a small number of agents to be very well connected and have a large amount of influence over the network (Garcia et al. 2017).
The network could instead be modelled using a preferential attachment model such as the Barabási-Albert algorithm (Barabási & Albert 1999), which generates a scale-free network with a few extremely well-connected hubs. However, this algorithm does not generate the high levels of clustering seen in real-world social networks. Further work could be done to examine the impact of using different types of networks.
The algorithm is implemented using the following steps:
- Each customer \(j\) is linked to their \(n_{K}\) nearest neighbours, \(n_{K}/2\) on each side, wrapping around to the start of the list at the end. This results in a regular ring-shaped network, with a total of \(n_{K}\) links per customer.
- For every customer \(j\), each \(n_{K}/2\) right-hand links \((j,k)\) are rewired with a probability \(\beta\). The new link \((j,k^{*})\) must not replicate an existing link. Additionally, a customer cannot be linked to itself.
As with the insurer agents, customers are randomly spaced along the preference space. The location assigned to a customer \(j\) is denoted \(L_{C,j}\). By the definition of the preference space (see Section 2.13), the shortest distance \(D_{ij}\) between customer \(j\) and insurer \(i\) is calculated according to Equation 5 below:
| \[ D_{ij}= Min\left(\left| L_{I,i} - L_{C,j}\right|,2-\left| L_{I,i} - L_{C,j}\right|\right)\] | \[(5)\] |
The variable \(Q_{ij0}\) represents customer \(j\)’s estimate of insurer \(i\)’s quality of service at time \(t=0\). At initialisation, these values are all set to \(0\), representing a neutral opinion.
Calculations
Assessing the cost of insurance. Similarly to the method used by Owadally et al. (2018) and Owadally et al. (2019), customers assess the cost of an insurance policy using not just the premium \(P_{ijt}\), but additional factors which matter to them. This total cost can be regarded as a disutility function.
Owadally et al. (2018) and Owadally et al. (2019) included the distance in a preference location space, calculated in a similar fashion to the distance \(D_{ij}\). This model also includes an allowance for service quality. Specifically, a customer \(j\) evaluates the cost of an insurance policy offered by insurer \(i\) at time \(t\) as a linear combination of: (a) the quoted premium \(P_{ijt}\) (b) the customer’s current (subjective) estimate of insurer \(i\)’s quality of service \(Q_{ijt}\) (described further in Equation 12 below) and (c) the preference cost \(D_{ij}\) the customer has for the insurer based on their relative positions in the preference landscape. This is captured in Equation 6 below:
| \[ C_{ijt}=P_{ijt} -k_{Q}Q_{ijt}+k_{D}D_{ij}\] | \[(6)\] |
Deciding whether to renew. Searching and comparing insurer premium quotes carries with it a cost in time and energy. Customers therefore commonly prefer to renew unless they believe they can obtain a significant decrease in cost by searching elsewhere (FCA 2020).
The decision whether or not renew an existing insurance contract is modelled as a probability. The value of this probability depends on the perceived change in the value of the contract. This probability is modelled using a logit function, which is a common choice (Günther et al. 2014). The probability of renewal \(r_{jt}\) for customer \(j\) at time \(t\) according to Equation 7 where \(\delta C_{ijt}=\frac{C_{ijt}-C_{ijt-1}}{C_{ijt-1}}\) is the rate of increase in customer \(j\)’s estimated cost of their renewed insurance contract with insurer \(i\) at time \(t\) (see Equation 6).
| \[ r_{jt}\;=\;1\left/\left(1+e^{a \delta C_{ijt} + b}\right)\right.\] | \[(7)\] |
Selecting a new insurer. If a customer decides not to renew their existing contract, they will seek premium quotes from all insurers in the market and calculate the total cost \(C_{ijt}\) for all insurers. This cost is calculated as in Equation 6 and includes allowances for brand preference and estimated quality of service. The customer will then aim to minimise their disutility by purchasing from the insurer with the lowest total cost. If the lowest cost corresponds with their existing insurer and renewal price, then they will decide to renew after all. If there are multiple possible insurers offering the lowest cost, they select one of these insurers at random.
Figure 5 shows the pseudocode used to carry out the insurer selection. First, the customer agent calculates the total renewal cost and probability of renewal, and then decides whether to renew and return their existing insurer. Otherwise, they calculate the total cost for each insurer in turn, and select the lowest available option.

Making a claim. If a customer suffers a loss event which is covered by the insurance contract, they will make a claim from their insurer. The frequency of these claims are modelled using a Poisson distribution, and the size is modelled using a Gamma distribution. These are common distributions used to model insurance claims (Jørgensen & Paes De Souza 1994).
When a customer makes a claim, they interact with their insurer’s customer service department. Consider a pair \((i,j)\) consisting of customer \(j\) and insurer \(i\). Define:
| \[\begin{aligned} s_{kt}\;=\;&\mbox{the outcome of the $k^{th}$ service experienced by customer} \\ &\mbox{$j$ interacting directly with insurer $i$ in the year $(t-1,t)$}\end{aligned}\] | \[(8)\] |
The value of each interaction \(s_{kt}\) is \(+1\) if the customer had a positive experience, and \(-1\) if the interaction was negative. Note that a customer can only collect more experiences with a particular insurer in time \(t\) if it has an insurance contract with them.
Word of mouth from the social network. Consider a pair of customers, \(j\) and \(j'\), who are linked by the social network generated at the start of the simulation. During a year, there is a probability \(p_{W}\) that customer \(j\) will share \(Q_{ijt}\), their current opinion of insurer \(i\), with their friend \(j'\). Similarly, \(j'\) will share their own opinion \(Q_{ij't}\) with the same probability. The word-of-mouth opinions act as another source of information for customer \(j\).
As with the service experiences, we can simplify the notation for a pair \((i,j)\) consisting of an insurer \(i\) and customer \(j\). Define:
| \[\begin{aligned} w_{kt}\;=\;&\mbox{the value of the $k^{th}$ word-of-mouth opinion received by customer} \\ &\mbox{$j$ interacting indirectly with insurer $i$ in the year $(t-1,t)$}\end{aligned}\] | \[(9)\] |
Note that if a customer has no opinion about an insurer because they have received no word-of-mouth information and also have had no direct experiences themselves (as will be the case at the start of the first time step), they will not pass on any information.
Figure 6 shows the pseudocode run by each customer agent in order to obtain and record word-of-mouth information during a timestep.

Opinion of insurer quality. As before, consider a pair \((i,j)\) consisting of an insurer \(i\) and customer \(j\). In any given year \((t-1,t)\), \(j\) receives information about \(i\) from a finite number of direct and indirect interactions. It is convenient to collect them in two vectors of finite length:
| \[\boldsymbol{s}_{t}=\left\lbrace s_{1t},s_{2t},s_{3t},...\right\rbrace^{'}\] | \[(10)\] |
| \[\boldsymbol{w}_{t}= \left\lbrace w_{1t},w_{2t},w_{3t},...\right\rbrace^{'}\] | \[(11)\] |
We define two vector functions, \(d:\mathbb{R}^{k}\mapsto\mathbb{R}\) and \(a: \mathbb{R}^{k}\mapsto\mathbb{R}\) for some \(k\in\mathbb{N}\). The former describes the length of a vector, and the latter the sum of all the elements of a vector. Consequently, \(d(\boldsymbol{s}_{t})\) is the number of direct claims interactions that customer \(j\) has in relation to insurer \(i\) in year \((t-1,t)\) and \(a(\boldsymbol{s}_{t})\) is the sum total of the outcome of these interactions. If customer \(j\) has no direct experiences with insurer \(i\) in year \((t-1,t)\), then \(\boldsymbol{s}_{t}\) is empty, and we assume that \(d(\boldsymbol{s}_{t})=a(\boldsymbol{s}_{t})=0\). Likewise for \(\boldsymbol{w}_{t}\) if the customer receives no word-of-mouth information about this insurer during the year.
It is a common assumption that agents in a dynamic market will weight newer information more highly than old information (Sutton & Barto 2018). This is consistent with the fading of human memory and a sensible approach when parameters and conditions may change over time. Though the insurer agents in this model maintain a constant customer service quality, insurers in the real market may enact dynamic strategies. It is therefore reasonable to weight each piece of information according to a memory factor \(\varphi^{t-\tau}\) where \(t\) is the current time and \(\tau\) is the time at which the information was received and \(0<\varphi<1\). The closer \(\varphi\) is to \(0\), the less weight the agents will place on older information.
It is also usual for humans to weight their own experience more highly than the opinions of others. For example, agents in opinion dynamic models take their own opinions as a starting point and move in the direction of other opinions during interactions with other agents with a weight proportional to the agents’ affinities for each other (Deffuant et al. 2002). Similarly, we will place a higher weight on an insurer’s own experiences \(\boldsymbol{s}_{t}\) than on the indirect information \(\boldsymbol{w}_{t}\).
By weighting each piece of information as described at the end of each time period, customer \(j\) updates their opinion \(Q_{ijt}\) of insurer \(i\)’s quality of service according to the Equation 12 below:
| \[ Q_{ijt}=\frac{\left(1-k_{W}\right)\sum_{\tau=1}^{t}\varphi^{t-\tau}a(\boldsymbol{s}_{\tau}) + k_{W}\sum_{\tau=1}^{t}\varphi^{t-\tau}a(\boldsymbol{w}_{\tau})}{\left(1-k_{W}\right)\sum_{\tau=1}^{t}\varphi^{t-\tau}d(\boldsymbol{s}_{\tau}) + k_{W}\sum_{\tau=1}^{t}\varphi^{t-\tau}d(\boldsymbol{w}_{\tau})}\] | \[(12)\] |
At \(t=0\), \(Q_{ij0}=0\); i.e. all customers begin with a neutral opinion of all insurers until one of them makes a claim and has either a good or bad experience. As each customer will pass on their \(Q_{ijt}\) values by word-of-mouth, information is passed around clusters of friends and will be assimilated into their own estimates at the end of the timestep. Note that as \(Q_{ijt}\) is ultimately a weighted average of claim interaction experience outcomes, it is bounded \((-1,+1)\).
Figure 7 shows the pseudocode of a customer agent updating their opinion. Note that instead of re-calculating the complete sum of all information each time, \(Q_{ijt}\) can be calculated as an update to the existing value \(Q_{ijt-1}\) by keeping track of the totals used in both the numerator and denominator. The pseudocode demonstrates this update and subsequent calculation for each insurer \(i\).

Outputs
- \(S_{ijt}\): Customer \(j\)’s opinion of insurer \(i\) at the start of time \(t\) based only on their own experiences. This is defined by:
\[S_{ijt}=\frac{\sum_{\tau=1}^{t}\varphi^{t-\tau}a(\boldsymbol{s}_{\tau})}{\sum_{\tau=1}^{t}\varphi^{t-\tau}d(\boldsymbol{s}_{\tau})}\] \[(13)\] - \(W_{ijt}\): Customer \(j\)’s opinion of insurer \(i\) at the start of time \(t\) based only on the word-of-mouth information received from their social network. This is defined by:
\[W_{ijt}=\frac{\sum_{\tau=1}^{t}\varphi^{t-\tau}a(\boldsymbol{w}_{\tau})}{\sum_{\tau=1}^{t}\varphi^{t-\tau}d(\boldsymbol{w}_{\tau})}\] \[(14)\] - \(Q_{ijt}\): Customer \(j\)’s overall opinion of insurer \(i\) at the start of time \(t\) based on a mixture of their own experiences and word-of-mouth information.
- \(Q_{jt}\): Customer satisfaction. This is customer \(j\)’s opinion of their current insurer at time \(t\).
- \(\delta_{jt}\): An indicator variable which is equal to \(1\) if customer \(j\) decided to renew at time \(t\), and 0 otherwise.
Data, Parameterisation and Validation
Data
This model is based where possible on data from the UK motor insurance market. However, in some places this data was not available, and US motor data has been used as a proxy. These data sources are listed here.
- The FCA report into insurer pricing practices (FCA 2020) is used as a data source regarding renewal behaviour. This report includes information about how insurance prices for existing customers seeking a renewal compare with the prices quoted for new customers, and the likelihood that customers choose to renew their existing contracts. It also mentions a proposed regulatory change, which is used here as an alternative scenario.
- The market level data of premium and losses is taken from a summary of EIOPA Solvency I submissions (EIOPA 2016). This data is for the years 2006-2015.
- To adjust these values to a comparable level, CPI data is used to inflate the historical values. Note that as the data is in Euros, the European CPI data is used (King 2021).
- Summary statistics from a dataset of facebook social circles collected by Stanford (Leskovec & Krevl 2014) are used to parameterise the word-of-mouth-network.
- A set of statistical data of US insurance companies’ historical advertising spending has been taken from Statista (Statista 2020a), a market and consumer data company.
- Statista was also used to obtain data on the market share of the top ten insurers in the UK motor insurance market (Statista 2020b).
- Data from the Insurance Information Institute about how often customers tend to make insurance claims per year (Insurance Information Institute 2019).
- This was supplemented by the Allstate claims information available on Kaggle (2016), which provided information about the shape of the severity distribution of motor claims (note: this is US data but was used as a proxy for the variation of claims).
- Information about the number of motorists in the UK was taken from the Society of Motor Manufacturers & Traders (The Society of Motor Manufacturers and Traders Limited 2020).
Parameterisation
Market parameters
Simulating 35 million customers as individual agents would require a prohibitive amount of computing power. However, the network will have a similar clustering co-efficient if it is sufficiently large to satisfy \(n_{c}>>n_{K}\) (Barrat & Weigt 2000), and remain connected if \(n_{K}>>\ln{n_{c}}>>1\) (Watts & Strogatz 1998). Based on this requirement, the number of customers \(n_{c}\) is set at \(10,000\).
Owadally et al. (2019) use \(20\) insurer agents, noting that the top twenty insurers hold a significant majority of the market share in the UK motor insurance market and is a reasonable number for producing computationally tractable yet realistic simulation dynamics. Similarly, the number of insurers \(n_{I}\) is set to \(20\).
As \(n_{C}\) does not represent the actual number of individual customers, we choose to rescale the inflation adjusted market data from Europa so that the average loss per representative customer agent is \(100\). An AR(2) curve is fitted to the rescaled market premium to find the values of \(\theta_{0}\), \(\theta_{1}\), and \(\theta_{2}\). The parameter \(\sigma_{M}\) is set as an unbiased estimate of the standard deviation of the residuals. Finally, the \(P_{-1}\) and \(P_{-2}\) are set as the last two available rescaled market premium values.
Insurer parameters
The maximum effective spending level is based on the largest level of spend on advertising per premium in a set of statistical data of US insurance companies (Statista 2020a). This gives a maximum service spend of approximately \(5\%\) of the expected premium level per premium.
As herding behaviour is common in markets, the base model assumes homogeneous service quality where all insurers spend the same amount per customer on customer service. Later the model is run with heterogeneous markets where insurers are assigned differing levels of service spend. The base model uses a value of \(E_{i}=0.8\). This indicates that most insurance interactions are generally positive, but insurers are not perfect and about 1 in 5 experiences are negative.
The FCA report into insurer pricing practices (FCA 2020) indicates that most of the increase in prices for renewing customer take place over the first 5 years, so we will set maximum term of markup increase \(T=5\). Additionally, the FCA report indicates that that the total average increase over that time is \(30\%\) of the customer premium, giving us an annual increase of \(R\) approximately \(5\%\).
Customer parameters
Approximately one in two people in the UK own a registered car (The Society of Motor Manufacturers and Traders Limited 2020). Additionally, studies demonstrate that the median number of social links per person is approximately 231 (McCarty et al. 2001). Based on these data, the average number of links per customer \(n_{K}\) is set at \(100\).
For a Watts-Strogatz network, the global clustering coefficient is approximately equal to \(\frac{3(n_{K}-2)}{2(2n_{K}-1)}\left(1-\beta\right)^{3}\) for large \(n_{c}\). Stanford examined various online social networks and found a global clustering coefficient of approximately \(0.2647\) (Leskovec & Krevl 2014). Based on this value and the chosen value of the parameter \(n_{K}\) the probability of rewiring \(\beta\) is set at \(0.3\).
For renewal behaviour, the parameters \(a\) and \(b\) are calibrated using two reference points. The average retention rate for the UK motor insurance market is approximately \(50\%\) (FCA 2020), so the standard renewal increase of \(5\%\) is assumed to correspond with a renewal probability of \(50\%\). For the second reference point, note that this report also tells us that customers consider the cost of searching for a new insurer to be worth £\(42\), or \(15\%\) of the average cost of an insurance policy. Based on this piece of data, the probability of renewal if the cost increases by \(15\%\) is set at half the usual rate, or \(25\%\).
The average claims frequency per customer \(\mu_{f}\) will dictate how many times a customer will interact with an insurer’s service quality and thus is an important parameter. This is set based on data from the Insurance Information Institute (Insurance Information Institute 2019). The average severity \(\mu_{s}\) is then calculated such that the total average loss per customer is \(100\) to match the market rescaling. Finally, to find a coefficient of variation, a distribution is fitted to the Allstate claims information available on Kaggle (2016); this determines the parameter \(\sigma_{S}\). These pieces of information are then used to parameterise a Gamma severity distribution.
Behavioural parameters
The remaining parameters are behavioural and thus are difficult to parameterise based on data:
- \(k_{Q}\), the sensitivity of a customer to an insurer’s customer service quality
- \(k_{D}\), the sensitivity of a customer to an insurer’s brand
- \(k_W\), the relative influence of word-of-mouth versus direct experience
- \(\varphi\), the rate at which old information is forgotten
- \(p_{W}\), the probability of a customer passing on word-of-mouth about a particular insurer to a friend
These factors are given reasonable estimates for a base model based on judgement. As these are judgement based, the model is also run for different values of the sensitivity parameters to test the effect of different assumptions on the results.
Customer survey data suggests that, though service quality has a significant influence on customer decisions, price remains the largest factor (Ansari & Riasi 2016; Ghodrati & Taghizad 2014; Tsoukatos & Rand 2006). The sensitivity coefficients are therefore set according to a reasonable increase in insurance prices. This is calculated as a year’s renewal markup on a premium increase of two standard deviations. This places limits on these values as:
| \[0<k_{D}<k_{Q}<32.65\] | \[(15)\] |
\(k_{W}\) is set to \(20\%\). This means that a piece of information \(s_{kt}\) obtained from direct experience is given a weighting of \(80\%\) relative to the weighting \(20\%\) of an indirect piece of word-of-mouth information \(w_{kt}\). Thus, it would take contrary information from at least four friends to counterbalance an opinion based on one piece of direct experience.
\(\varphi\) is a memory factor. The higher the value of \(\varphi\), the greater the weight a customer places on older pieces of information. If \(\varphi=0\) then all estimates are based on the latest information only, and if \(\varphi=1\) the customer places equal weight on all pieced of information regardless of when they occurred. For the ‘base’ model, a value of \(\varphi=60\%\) is used. This means a given piece of information which is now five years old is given a weighting just less than \(10\%\) of that given to recent information.
\(p_{W}\) is set equal to \(5\%\). As the average number of links \(n_{K}\) is set to \(100\), this indicates than on average, customers will seek an opinion from \(5\) friends a year on a particular insurer.
Validation
In the real world, firm size often follows an uneven distribution, with a few insurers taking a significant proportion of the available market share (Gabaix 2009). This pattern can also be seen in the real world market share of the top 10 UK motor insurers (Statista 2020b). This data can therefore be used to validate the model by comparison with the modelled distribution of insurer share.
Preliminary regression tests indicate that the key parameter values which determine the shape of this distribution are the relative ratios of the customer cost sensitivity parameters \(k_{D}\) and \(k_{Q}\). Variations of the base model were run while this ratio was varied, and a ratio of \(\frac{k_{Q}}{k_{D}}=2.2\) was found to minimise the squared distance of the average simulated market shares and the empirical market data to within two significant figures.
To validate this output, we perform a Kolmogorov-Smirnoff test1 with the initial hypothesis
| \[\begin{aligned} H_{0} : & \mbox{ the real-world top 10 market shares are drawn from the same} \\ & \mbox{ distribution as the top 10 market shares in the model}\end{aligned}\] | \[(16)\] |
To apply this test, we compare the sample of ten real-world values with the distribution of market shares for the top 10 insurers across 300 simulations. The results are ignored for the first 20 timesteps as the model is still settling into equilibrium, and otherwise included for a further 80 timesteps, giving a total of 120,000 datapoints.
This gives us a test statistic of 0.231, at a p-value of 0.584. This is not enough to reject the initial hypothesis at even a strict 80% level. We thus accept that this model produces market share outputs which follow a similar distribution to those produced in the real-world.
From this validation exercise, \(k_{Q}\) is equal to \(2.2k_{D}\). From our earlier reasoning, this puts an upper bound on \(k_{D}\) of \(15\). For the base model, \(k_{D}=10\) and \(k_{Q}=22\).
Looking at the customer’s estimation of service quality (Equation 12), we might naively conclude that this is an unbiased estimate of the expected outcome of an interaction with an insurer in the event of a claim. As all word-of-mouth information is equal to a friend’s own opinion \(Q_{ijt-1}\), the value of \(Q_{ijt}\) is calculated as a weighted average of experiences (unless the customer has no information at all as yet).
However, the existence of the word-of-mouth network can lead to systemic bias. To see this, consider a simple example where there are two customers and two insurers. The value of \(k_{w}\) is \(20\%\), \(\varphi=60\%\), and both customers always pass information between them. To start with, the two customers have a neutral opinion; customer 1 selects insurer 1, and customer 2 selects insurer 2. Both customers have an \(80\%\) chance of good customer service, and \(20\%\) chance of bad customer service.
In the first time step, customer 1 makes a claim, and by chance experiences bad service. Customer 2 also makes a claim, but has a good experience. As a result, customer 1 decides not to renew. Their opinion of insurer 1 is now at \(-1\) based on their only information, so they select insurer 2 over insurer 1. The two friends then exchange word-of-mouth information. They now both hold an opinion of \(-1\) on insurer 1, and \(+1\) on insurer 2. After they have both been with insurer \(2\) for a further three years, customer 1 has a bad experience with insurer 2.
However, customer 1 and 2 have been exchanging word-of-mouth information every year, reinforcing their established opinion by repeating it between themselves. This new information means that customer 1’s opinion of insurer 2 is now:
| \[Q_{214}\;=\;\frac{0.8(-1) + 0.2(+1 +0.6 1 + 0.6^{2} 1)}{0.8+ 0.2(1 +0.6 + 0.6^{2})} \;=\; -0.34\] | \[(17)\] |
From this we can see that this is only a third as negative as their opinion of insurer 1. In this case, the gain in premium from becoming a new customer is not enough to offset the perceived decrease in quality, and customer 1 decides not to switch.
If both customers remain with insurer 2, then over time, they will amass enough information to get an accurate opinion. Although the initial opinion will be passed around as with insurer 1, the long term equilibrium state tends toward the true value as we would expect. This will solidify the perceived gap between insurer 2 and insurer 1, and it would be very rare and fleeting for either customer to ever again purchase from insurer 1.
The persistence of negative opinions through the word-of-mouth network and the rarity of obtaining corrective information causes a similar effect on a large scale in the model, causing a systemic bias in the estimated service quality. We thus see that the expected value of \(Q_{ijt}\) is in fact a little lower than the true value, unless the true value is either \(0\) or \(1\), in which case there is no variance in outcomes and all opinions are correct. The size of the bias will depend on the shape of the network and how efficiently information is spread through it.
Without this effect, we would expect that in a market where insurers are spending the same amount on customer service, they would take an equal share of the customers. However, this systemic effect can cause some opinions based on a small number of experiences to persist in the market, causing some insurers to be unfairly favoured over others. As a result, the market share follows a distribution, with some insurers taking a greater or lesser market share.
Scenarios
Base model
The model is implemented in C#. The inbuilt Random class was used to generate random numbers and is based on a modified version of Knuth’s subtractive random number generator algorithm (Knuth 1997). All models are run for \(100\) time steps, and \(300\) simulations. The starting seed is specified by an input file, and is used consistently across different sensitivity tests and scenarios, making these results directly comparable.
The parameters used in the base model are taken from the parameterisation and validation process described above and listed in Table 1.
| Parameter | Description | Value |
|---|---|---|
| \(n_{I}\) | No. of insurers | \(20\) |
| \(n_{C}\) | No. of customers | \(10,000\) |
| \(k\) | No. of links per customer | \(100\) |
| \(\beta\) | Rewiring probability in social network | \(30\%\) |
| \(\overline{P}_{-1}\) | Market premium in year -1 | \(91.85\) |
| \(\overline{P}_{-2}\) | Market premium in year -2 | \(89.28\) |
| \(\theta_{0}\) | Coefficient in AR(2) process for market premium | \(76.03\) |
| \(\theta_{1}\) | Coefficient in AR(2) process for market premium | \(0.6675\) |
| \(\theta_{2}\) | Coefficient in AR(2) process for market premium | \(-0.3580\) |
| \(\sigma_{M}\) | Stochastic variability for market premium | \(14.19\) |
| \(E\) | Max insurer spending on customer service per customer | \(5.83\) |
| \(E_{i}\) | Level of annual insurer spend on customer service per customer | 4.664 |
| \(R\) | Renewal markup | \(5\%\) |
| \(T\) | Max renewal term | \(5\) |
| \(a\) | Renewal probability scaling | \(10.986\) |
| \(b\) | Renewal probability shift | \(-0.5493\) |
| \(k_{Q}\) | Customer service sensitivity | \(22\) |
| \(k_{D}\) | Customer preference sensitivity | \(10\) |
| \(\varphi\) | Memory factor | \(60\%\) |
| \(k_{W}\) | Word-of-mouth influence factor | \(20\%\) |
| \(\mu_{f}\) | Average loss frequency per customer | \(13\%\) |
| \(\mu_{s}\) | Average loss severity | \(755.8\) |
| \(\sigma_{s}\) | Standard deviation of loss severity | \(730.1\) |
| \(p_{W}\) | Probability of word-of-mouth transmission | \(5\%\) |
Sensitivity tests
Additionally, several sensitivity tests are run to explore the effect of changing some of the key behavioural parameters. The range of these tests are described in Table 2.
| Parameter | Values |
|---|---|
| \(E_{i}/E\) | 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.9 |
| \(k_{Q}\) | 14, 16, 18, 20, 24, 26, 28, 30 |
| \(k_{D}\) | 6, 8, 12, 14, 16, 18, 20, 22 |
| \(k_{W}\) | 0.05, 0.1, 0.15, 0.25, 0.3, 0.35, 0.4, 0.45 |
| \(\varphi\) | 0.1, 0.2, 0.3, 0.4, 0.5, 0.7, 0.8, 0.9 |
| \(p_{W}\) | 0.02, 0.03, 0.04, 0.06, 0.07, 0.08, 0.09, 0.1 |
Heterogeneity of insurer spending
This model does not allow for insurer strategies around service quality spend. However, possible variations can be examined by running models with heterogeneous service quality. This is done by randomly assigning each insurer a constant value of \(E_{i}\) in increments of \(0.05E\). In order to get a large enough range of scenarios generated in this way, this model is run for \(1,000\) simulations.
Additionally, the heterogeneous model is run for varying values of \(k_{Q}\) as in the sensitivity tests.
Regulation change scenario
The FCA report (FCA 2020) also proposed an enforced change to insurer pricing whereby a customer who renews their policy must not be charged more than if they were a new customer. This scenario is also run in the model, and the results compared with those of the base model.
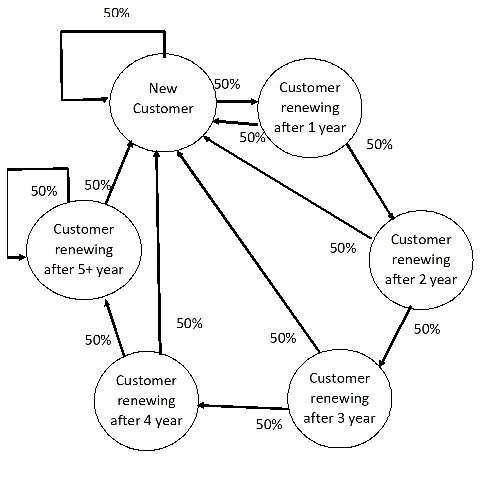
Without the expected discount for new customers, the insurers will increase their premium overall. To account for this, we model the customers’ renewal states as a Markov chain with a \(50\%\) chance of returning to \(0\) years from each state (see Figure 8). Multiplying these out by the appropriate renewal premium markup give us an expected overall premium of: \(\overline{P}_{t}\sum_{i=0}^{i=5}\frac{1}{2^{min(i+1,5)}}1.05^{min(i,5)}\). This gives an increase factor of \(5.05\%\).
Results
Base model
As described earlier, the market opinion of an insurer based on experiences in the first few years persists as it gets passed around friendship groups and reinforced each time a customer hears the same information from a friend. This phenomenon, alongside the comparative rarity of new experiences, makes it difficult for an insurer who had an unfortunate early record to attract enough new customers to override the low opinion.
Regression analyses are carried out on the simulated model outputs to elicit an understanding of the variables that drive its behaviour. Table 3 shows the results of a regression on the average outputs across each simulation versus the average quality of experiences in the first time step for each insurer. This table shows that as expected from the systemic bias described above, the initial performance is a significant factor with a high goodness of fit on an insurer’s subsequent reputation, market share, and renewal rate.
| Output \(y_{it}\) | Intercept \(\alpha_{0}\) | Slope \(\alpha_{1}\) | p-value | \(R^{2}\) |
|---|---|---|---|---|
| Insurer reputation \(Q_{ijt}\) | \(0.146\) | \(73.3\%\) | \(0\) | \(0.802\) |
| Insurer market share \(m_{s,it}/n_{c}\) | \(-18.4\%\) | \(39.1\%\) | \(0.000\) | \(0.611\) |
| Insurer renewal rate \(R_{it}\) | \(-25.5\%\) | \(108.4\%\) | \(0.000\) | \(0.385\) |
As we would expect, though the average retention rate is close to 50%, it varies throughout the simulation along with the change in market premium. When the premium is increasing, retention rates go down as customers see the increase and seek out new quotes. When it is decreasing, retention rates increase as even with a markup, the renewal premium is not a significant increase. This relationship can be seen in the results of a regression carried out on each individual timestep for each simulation of the base model. These results are shown in Table 4. As a result, insurers who maintain good service quality while premiums are rising may suffer a decline in renewal rates if they also pass that expense along to their customers, yet are unlikely to benefit if their reputation has already been well established.
| Intercept \(\alpha_{0}\) | Slope \(\alpha_{1}\) | p-Value | \(R^{2}\) |
|---|---|---|---|
| \(144.7\%\) | \(-0.876\%\) | \(0.000\) | \(0.239\) |
Sensitivity tests
Service spend
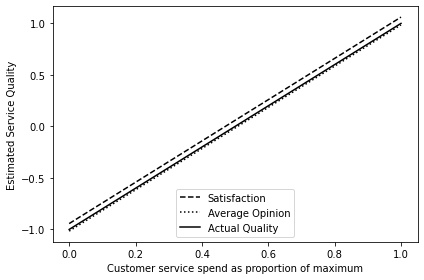
As we would expect, the main impact of increasing the insurer’s chosen customer service spend relative to the maximum spend is to increase the customer’s opinion of the insurers. This is because the higher the spend, the higher the insurers’ service quality. Table 5 shows the p-values and goodness of fit of this regression relationship for both the customer satisfaction — which is the customers’ opinion of their own insurer — and also for the average customer’s opinion of all insurers. From this table, we see evidence of the bias that causes the unequal market concentrations: the customer satisfaction regression line lies just above the true value, and the average opinion of all insurers lay below it. This can be seen in Figure 9.
Additionally, the retention rates show a greater variation as \(E_{i}\) is increased. This is because the main driver of retention rates is the change in premium, which increases along with service spend. As a result, insurers who maintain good service quality while premiums are rising may suffer a decline in renewal rates if they also pass that expense along to their customers, yet are unlikely to benefit if their reputation has already been well established.
| Output \(y_{k}\) | Intercept \(\alpha_{0}\) | Slope \(\alpha_{1}\) | p-value | \(R^{2}\) |
|---|---|---|---|---|
| Average of \(Q_{it}\) (Customer satisfaction) | -0.943 | 2.004 | 0.000 | 0.997 |
| Average of \(Q_{ijt}\) (Customer opinions of all insurers) | -0.1.016 | 2.001 | 0.000 | 0.975 |
| Standard deviation of \(\overline{R}_{t}\) (market renewal rate) | \(27.3\%\) | \(5.11\%\) | \(0.000\) | 0.383 |
Preference and service sensitivities
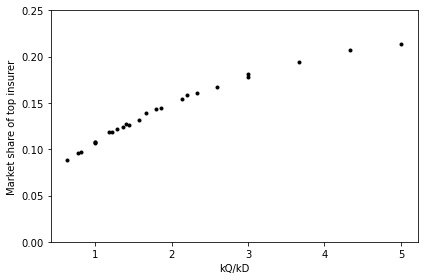
As discussed in the validation section, the main impact of these parameters is on the concentration of the market shares between the insurers. When \(k_{D}\) is high and \(k_{Q}\) is low, customers are more heavily influenced by their location on the brand preference space. Since the agents were evenly spread out among this space, this creates a market concentration close to even (i.e. \(5\%\) for each of the 20 insurers). The higher the value of the service sensitivity \(k_{Q}\) relative to the preference sensitivity \(k_{D}\), the more the customers’ choice of insurer is influenced by their opinion of an insurer’s customer service quality, leading to a more unequal market concentration (Figure 10). Table 6 demonstrates the results of a regression on the value of the market share of the top insurer respective to the ratio of these sensitivities, and shows that this is a significant relationship which gives a strong fit.
| Intercept \(\alpha_{0}\) | Slope \(\alpha_{1}\) | p-Value | \(R^{2}\) |
|---|---|---|---|
| \(8.21\%\) | \(3.02\%\) | \(0.000\) | \(0.675\) |
Influence factor and transmission rate
If either the influence factor \(k_{W}\) or the word-of-mouth transmission rate \(p_{W}\) is set to zero, then there is no transmission of word-of-mouth information. In that case, the market concentration becomes more evenly spread, giving a top market share of 5.5%. Additionally, the average customer opinion of an individual insurer is close to zero as most customers do not have any information about a particular insurer. However, it does not require a very high value before information reaches saturation and the consensus market opinion becomes close to the true value. This is seen in Figure 11.
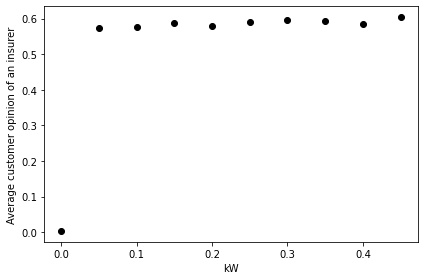
Table 7 displays the results of regression on the word-of-mouth influence factor \(k_W\) and on the word-of-mouth transmission rate \(p_W\). We see that although \(k_{W}\) and \(p_{W}\) are significant factors for both the top insurer’s market share and the customer satisfaction, the goodness of fit \(R^{2}\) is low. Additionally, the slope is quite shallow in comparison with the size of the parameter change. The regression model suggests that the top insurer’s market share varies between 13% and 18% for the \(k_{W}\) sensitivity tests, and the average customer satisfaction varies between 65% and 67%. For the \(p_{W}\) sensitivity tests, the top insurer’s market share varies between 14% and 18%, and the average customer satisfaction varies between 64% and 67%.
| Output \(y_{t}\) | Input \(x_{k}\) | Intercept \(\alpha_{0}\) | Slope \(\alpha_{1}\) | p-Value | \(R^{2}\) |
|---|---|---|---|---|---|
| Top insurer market share | \(k_{W}\) | \(12.6\%\) | \(12.7\%\) | \(0.000\) | \(0.279\) |
| Customer satisfaction | \(k_{W}\) | \(64.2\%\) | \(6.95\%\) | \(0.000\) | \(0.168\) |
| Top insurer market share | \(p_{W}\) | \(13.0\%\) | \(47.0\%\) | \(0.000\) | \(0.182\) |
| Customer satisfaction | \(p_{W}\) | \(63.2\%\) | \(42.0\%\) | \(0.000\) | \(0.228\) |
Memory factor
Without the word-of-mouth network, we would expect that a low memory factor \(\varphi\) would lead to a more equal market share as old experiences do not have a high influence on opinion. However, although a regression shows that \(\varphi\) is a significant factor in the market share of the top insurer, the regression coefficient for the slope is low (\(3.45\%\)), and the intercept is not close to an equal split of \(5\%\) (see Table 8). This reflects the effect of the word-of-mouth network, which circulates the experiences and maintains a systemic memory.
| Intercept \(\alpha_{0}\) | Slope \(\alpha_{1}\) | p-Value | \(R^{2}\) |
|---|---|---|---|
| \(13.8\%\) | \(3.45\%\) | \(0.000\) | \(0.118\) |
Heterogeneity of customer service
The base model was simulated 1,000 times. In each simulation, each insurer \(i\) is randomly assigned a customer service spend \(E_{i}\) which is constant over time \(t\) and which is drawn equally likely from the set \(\{ 0, 0.05 E, 0.1 E, 0.15 E, \cdots , E \}\).
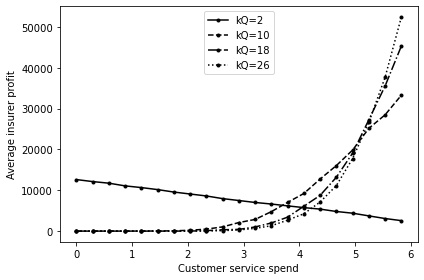
Looking at the profit averaged across all scenarios, broken down by \(E_{i}\), we find that the companies assigned a value of \(E_{i}\) less than \(75\%\) of the maximum spend \(E\) are usually unable to compete with the insurers who spent more money. Despite the increased cost that is passed on to the customer, under the base model parameterisation, the optimal setting is consistently set at the maximum value \(E\). Higher quality insurers attract both a higher renewal rate and a higher number of new sales.
Figure 12 shows that, as customer service spend increases, the average insurer profit increases, except at very low levels of customer sensitivity to service quality \(k_Q\). In general, Figure 12 demonstrates that the highest average profit is achieved by insurers when they spend the most on customer service.
Regulation change
We also consider the possible implications of the proposed regulation change by comparing the results of this model with those of the base model, including the results of the sensitivity tests. This was done by performing a series of regressions using indicator variables and testing these variables for significance; i.e.: \(y_{k} = \alpha_{0} + \alpha_{1}x_{k} + \alpha_{2}I_{k} + \alpha_{3}I_{k}x_{k} + \epsilon_{k}\) where \(I_{k}\) is equal to \(0\) for an output from the base model and \(1\) for an output from a model with the regulation change. If the coefficient \(\alpha_{2}\) is significant, then it indicates a change in the average value of the output between the two models. If \(\alpha_{3}\) is significant, then it indicates a change in the relationship between the sensitivity parameter and the tested output.
Table 9 shows the significant results of this regression run excluding the sensitivity tests; i.e. the pure change between the base model and the regulatory scenario. Note that for these regressions, there is no variable \(x_{k}\), and so \(\alpha_{1} = \alpha_{3} = 0\). As we would expect, these results show a large increase in the average renewal rates for the regulation scenario and a decrease in their variability. There is also an increase in the top market share, suggesting a more unequal market concentration and thus a reduction in market competition. This is because in the base model, there was a small but steady number of customers willing to switch to a lower reputation insurer nearer their brand preference. After the regulation change, the rate of switching is much lower. As a result, the original experiences have more time to circulate among clusters, while there is simultaneously less new information available to the network to correct the initial bad impression.
| Output \(y_{k}\) | Intercept \(\alpha_{0}\) | Impact on intercept \(\alpha_{2}\) | p-Value | \(R^{2}\) |
|---|---|---|---|---|
| Average of top insurer’s market share | \(15.8\%\) | \(3.8\%\) | \(0.000\) | \(28.1\%\) |
| Standard deviation of top insurer’s market share | \(1.25\%\) | \(0.974\%\) | \(0.000\) | \(16.8\%\) |
| Average of market renewal rate | \(48\%\) | \(46.9\%\) | \(0.000\) | \(99.9\%\) |
| Standard deviation of market renewal rate | \(31.4\%\) | \(-27.6\%\) | \(0.000\) | \(99.3\%\) |
Table 10 shows the regression results for the sensitivity tests run on both the base model and the regulation scenario. Without the noise in renewal rates caused by changing market premium, a relationship can now be detected between renewal rates and the word-of-mouth influence parameters \(k_{W}\), \(M\), and \(p_{W}\). These parameters also have a higher impact on market concentration. The higher these values, the more information the customers are using to evaluate insurers, and the higher the renewal rates and unequal market concentration.
| Output \(y_{k}\) | Input \(x_{k}\) | Intercept \(\alpha_{0}\) | Slope \(\alpha_{1}\) | p-Value for \(\alpha_{1}\) | Impact on intercept \(\alpha_{2}\) | p-Value for \(\alpha_{2}\) | Impact on slope \(\alpha{3}\) | p_value for \(\alpha_{3}\) | \(R^{2}\) |
| Top share | \(k_W\) | \(12.6\%\) | \(12.7\%\) | \(0.000\) | \(1.95\%\) | \(0.000\) | \(9.69\%\) | \(0.000\) | \(47.6\%\) |
| Renewal rate | \(k_W\) | \(48.1\%\) | \(0.0287\%\) | \(0.806\) | \(45.7\%\) | \(0.000\) | \(5.16\%\) | \(0.000\) | \(99.9\%\) |
| Top share | \(\varphi\) | \(13.8\%\) | \(3.45\%\) | \(0.000\) | \(2.77\%\) | \(0.000\) | \(2.22\%\) | \(0.000\) | \(35.5\%\) |
| Renewal rate | \(\varphi\) | \(48\%\) | \(0.0596\%\) | \(0.314\) | \(43.7\%\) | \(0.000\) | \(5.34\%\) | \(0.000\) | \(99.9\%\) |
| Renewal rate | \(p_W\) | \(48\%\) | \(0.517\%\) | \(0.386\) | \(45.3\%\) | \(0.000\) | \(25.9\%\) | \(0.000\) | \(99.9\%\)< |
We also run a heterogeneous version of the regulatory change model. As with the base model, the optimal position is the maximum spend on customer service quality. By plotting the profit as a proportion of the market average, it can be seen that the relative advantage for the regulation scenario is larger than for the base model (see Figure 13).
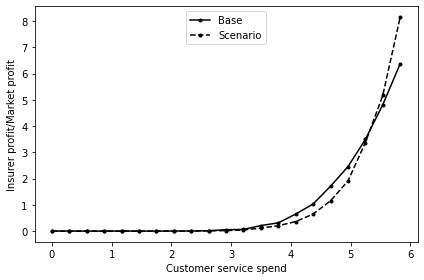
This is because without the additional premium increase from the renewal markup, customers are far less likely to be motivated to switch due to a change in price. Customer choices become instead much more influenced by their estimates of customer service quality. This implies that the regulatory change could also be an incentive to increase customer service quality.
Conclusions
An ABM was constructed to explore the patterns that might arise in an insurance market due to customers passing on their opinion of their insurer to their social network. The model is not intended to be a complete model of all of the features of an insurance market, nor should it be taken as a predictive model. Instead, it has been designed to focus on the particular features of customer renewal decisions when a word-of-mouth network is present, and to be informative of patterns and emergent dynamics.
Empirical data was used to parameterise the model, though this was not always possible for behavioural parameters. In these cases, reasonable values were proposed, and sensitivity tests carried out for these parameters. A validation check was carried out by comparing the model output of market concentrations against real world data.
The ABM notably replicates a key feature of the real-world market: it produces an uneven concentration of market share by insurer. This is because early variations in customer service experiences persist in the market opinion as information is repeatedly repeated and passed around within social groups. Because interaction is rare, it takes some time for an individual to correct a biased perception once they select a new insurer. As a result, some insurers gain a better or worse reputation than others even when they have the same service quality. This phenomenon also causes the average customer’s opinion of their own insurer to be higher than their true service quality. This suggests that new insurers particularly benefit from having a high service quality as they establish their reputation.
As we would expect, the biggest driver in customers’ decision whether to renew is the change in market premium. This is exacerbated when the insurers are charging a larger margin for service quality. As a result, insurers who maintain good service quality while premiums are rising may suffer a decline in renewal rates if they also pass that expense along to their customers, yet are unlikely to benefit if their reputation has already been well established.
If the insurers are allowed to have different service qualities, their relative success depends on the customers’ sensitivity to service quality. In the base model, insurers with higher service quality do better as they both attract and retain more customers. If the customers are less sensitive to customer service relative to the cost, then the extra premium mitigates this effect, until eventually a higher customer quality is a detriment. However, only a small sensitivity value is required for higher customer service quality to become beneficial.
The UK regulatory authority (FCA 2020) has recently proposed a change in regulations that would prevent UK motor insurers from charging renewing customers a different amount than they would if they were new customers. This change would be expected to cause a large increase in renewal rates as customers’ prices change less each year and they can expect less benefit from searching for quotes. Additionally, the relative advantage to insurers attempting to entice new customers with better quality customer service has increased. This implies that the proposed regulation change could also increase the incentive for better customer service quality to compete against rival insurers. However, when the retention rate is very high, customer choices are less influenced by the market cycle. There is much less movement away from insurers with a good reputation and fewer customers deciding to purchase from the lower valued insurers. As a result, the market concentration becomes more skewed. This indicates that the proposed regulatory change might decrease market competition.
Based on these findings, we can conclude that the potential impact of the word-of-mouth network on customer decision-making and the resulting systemic biases is a significant one. These findings should be considered by both insurers considering strategies for attracting and retaining customers, and by regulators who are assessing possible impacts of a change in the regulation of insurance pricing practices.
In future work, we intend to expand the model to allow the insurers to employ a competitive premium-setting strategy and vary their service quality or premium dynamically. The model also contains some implicit behavioural assumptions: for example, good and bad experiences are given the same weight, whereas many studies indicate that people are more sensitive to negative than positive experiences. Additionally, the word-of-mouth information in this model does not include a measure of uncertainty around the customers’ opinions. This could potentially change the network dynamics which lead to such a high persistence of opinions within social groups. Some experiments could also be carried out with different types of network and network sizes, to investigate if the current number of customer agents is sufficient to replicate the rate of information saturation and investigate how the word-of-mouth effects vary at different market scales.
Model Documentation
The model has been built in C#. The code is available here: https://www.comses.net/codebase-release/f94fdd87-7d70-480b-a9ac-6389239bd21c/.Notes
While we would prefer to run a test with a larger set of data, we do not have access to the data for other insurers (Statista 2020b). However, we note that the top ten insurers cover a total market share of \(85.8\%\), which is a significant majority of the total market.↩︎
References
ALKEMPER, J., & Mango, D. F. (2005). Concurrent simulation to explain reinsurance market price dynamics. Risk Management, 6, 13–17.
ANSARI, A., & Riasi, A. (2016). Modelling and evaluating customer loyalty using neural networks: Evidence from startup insurance companies. Future Business Journal, 2(1), 15–30. [doi:10.1016/j.fbj.2016.04.001]
BARABÁSI, A.-L., & Albert, R. (1999). Emergence of scaling in random networks. Science, 286(5439), 509–512.
BARRAT, A., & Weigt, M. (2000). On the properties of small-world network models. The European Physical Journal B - Condensed Matter and Complex Systems, 13(3), 547–560. [doi:10.1007/s100510050067]
BERGER, L. A. (1988). Word-of-mouth reputations in auto insurance markets. Journal of Economic Behavior & Organization, 10(2), 225–234. [doi:10.1016/0167-2681(88)90046-7]
BERGER, L. A., Kleindorfer, P. R., & Kunreuther, H. (1989). A dynamic model of the transmission of price information in auto insurance markets. Journal of Risk and Insurance, 56(1), 17–33. [doi:10.2307/253012]
BIANCHI, F., & Squazzoni, F. (2015). Agent-based models in sociology. Wiley Interdisciplinary Reviews: Computational Statistics, 7(4), 284–306. [doi:10.1002/wics.1356]
BOUCEK, C. H., & Conway, T. E. (2003). Dynamic pricing analysis. The Casualty Actuarial Society Forum Winter 2003 Edition Including the Data Management Call Papers and Ratemaking Discussion Papers. Available at: https://www.casact.org/sites/default/files/database/forum_03wforum_03wf161.pdf.
BOYER, M. M., & Owadally, I. (2015). Underwriting apophenia and cryptids: Are cycles statistical figments of our imagination? The Geneva Papers on Risk and Insurance-Issues and Practice, 40(2), 232–255. [doi:10.1057/gpp.2014.12]
CRABB, R., & Shapiro, A. F. (1996). Managing the insurance enterprise - An interactive computer game. Actuarial Research Clearing House, Volume 1: https://www.soa.org/globalassets/assets/library/research/actuarial-research-clearing-house/1990-99/1996/arch-1/arch96v122.pdf. [doi:10.1002/9780470012505.taa033]
CUMMINS, J. D., & Outreville, J. F. (1987). An international analysis of underwriting cycles in property-liability insurance. Journal of Risk and Insurance, 54(2), 246–262. [doi:10.2307/252856]
DEFFUANT, G., Amblard, F., Weisbuch, G., & Faure, T. (2002). How can extremism prevail? A study based on the relative agreement interaction model. Journal of Artificial Societies and Social Simulation, 5(4), 1: https://www.jasss.org/5/4/1.html. [doi:10.18564/jasss.2211]
DUBBELBOER, J., Nikolic, I., Jenkins, K., & Hall, J. (2017). An agent-based model of flood risk and insurance. Journal of Artificial Societies and Social Simulation, 20(1), 6: https://www.jasss.org/20/1/6.html. [doi:10.18564/jasss.3135]
EIOPA. (2016). Statistical time series (2005-2015) based on Solvency I. Available at: https://www.eiopa.europa.eu/content/european-insurance-overview-2018_en
ENGLAND, R., Owadally, I., & Wright, D. (2021). An Agent-Based Model of Insurance Customer Behaviour with Word of Mouth Network in C#. CoMSES Net, Version 1.0.0. Available at: https://www.comses.net/codebases/ab858bad-0a03-4935-9abd-6744821241b5/releases/1.0.0/.
FCA. (2020). General insurance pricing practices: Final report. Financial Conduct Authority, Volume MS18, Number 1.3. Available at: https://www.fca.org.uk/publication/market-studies/ms18-1-3.pdf.
FENN, P., & Vencappa, D. (2005). Cycles in insurance underwriting profits: Dynamic panel data results. CRIS Discussion Paper Series.
GABAIX, X. (2009). Power laws in economics and finance. Annual Review of Economics, 1(1), 255–294. [doi:10.1146/annurev.economics.050708.142940]
GARCIA, D., Mavrodiev, P., Casati, D., & Schweitzer, F. (2017). Understanding popularity, reputation, and social influence in the twitter society. Policy & Internet, 9(3), 343–364. [doi:10.1002/poi3.151]
GHODRATI, H., & Taghizad, G. (2014). Service quality effect on satisfaction and word of mouth in insurance industry. Management Science Letters, 4(8), 1765–1772. [doi:10.5267/j.msl.2014.7.007]
GIONTA, G. (2000). Insurance World II: A complex model for managing risk in the age of globalization. ItalRe Group. Available at: https://www.actuaries.org.uk/system/files/documents/pdf/Giuseppe.pdf.
GOLDENBERG, J., Libai, B., & Muller, E. (2001). Talk of the network: A complex systems look at the underlying process of word-of-mouth. Marketing Letters, 12(3), 211–223. [doi:10.1023/a:1011122126881]
GÜNTHER, C.-C., Tvete, I. F., Aas, K., Sandnes, G. I., & Borgan, Ø. (2014). Modelling and predicting customer churn from an insurance company. Scandinavian Actuarial Journal, 2014(1), 58–71.
HARRINGTON, S. E., & Niehaus, G. (2000). 'Volatility and underwriting cycles.' In G. Dionne (Ed.), Handbook of Insurance (pp. 657–686). Berlin Heidelberg: Springer. [doi:10.1007/978-94-010-0642-2_20]
HEINRICH, T., Sabuco, J., & Farmer, J. D. (2021). A simulation of the insurance industry: The problem of risk model homogeneity. Journal of Economic Interaction and Coordination, 1–42. [doi:10.1007/s11403-021-00319-4]
INSURANCE Information Institute. (2019). Facts + Statistics: Auto insurance. Available at: https://www.iii.org/fact-statistic/facts-statistics-auto-insurance;accessed10/12/2020.
JØRGENSEN, B., & Paes De Souza, M. C. (1994). Fitting Tweedie’s compound Poisson model to insurance claims data. Scandinavian Actuarial Journal, 1994(1), 69–93.
KAGGLE. (2016). Allstate Claims Severity. Available at: https://www.kaggle.com/c/allstate-claims-severity/data;accessed10/12/2020.
KING, A. (2021). HICP Annual Percentage Change - EU 28 2015=100. Office for National Statistics. Available at: https://www.ons.gov.uk/economy/inflationandpriceindices/timeseries/gj2e/mm23.
KNUTH, D. (1997). The Art of Computer Programming, Volume 2: Seminumerical Algorithms. Addison-Wesley Longman Publishing Co., Inc.
KOWALSKA-STYCZEŃ, A., & Sznajd-Weron, K. (2016). From consumer decision to market share-unanimity of majority? Journal of Artificial Societies and Social Simulation, 19(4), 10: https://www.jasss.org/19/4/10.html.
LESKOVEC, J., & Krevl, A. (2014). SNAP Datasets: Stanford Large Network Dataset Collection. Available at: http://snap.stanford.edu/data.
MCCARTY, C., Killworth, P. D., Bernard, H. R., Johnsen, E. C., & Shelley, G. A. (2001). Comparing two methods for estimating network size. Human Organization, 60(1), 28–39. [doi:10.17730/humo.60.1.efx5t9gjtgmga73y]
MILLS, A. (2010). Complexity science: An introduction (and invitation) for actuaries. Available at: https://www.soa.org/globalassets/assets/files/research/projects/research-complexity-report.pdf.
OWADALLY, I., Zhou, F., Otunba, R., Lin, J., & Wright, D. (2019). An agent-based system with temporal data mining for monitoring financial stability on insurance markets. Expert Systems with Applications, 123, 270–282. [doi:10.1016/j.eswa.2019.01.049]
OWADALLY, M., Zhou, F., & Wright, I. (2018). The insurance industry as a complex social system: Competition, cycles, and crises. Journal of Artificial Societies and Social Simulation, 21(4), 2: https://www.jasss.org/21/4/2.html. [doi:10.18564/jasss.3819]
PALIN, J., Silver, N., Slater, A., & Smith, A. D. (2008). Complexity economics application and relevance to actuarial work. Report of a working party of the UK actuarial profession. Paper presented to the Finance Investment and Risk Management Conference.
PARODI, P. (2012). Computational intelligence with applications to general insurance: A review. Annals of Actuarial Science, 6(2), 344–380. [doi:10.1017/s1748499512000048]
SMITH, K. A., Willis, R. J., & Brooks, M. (2000). An analysis of customer retention and insurance claim patterns using data mining: A case study. Journal of the Operational Research Society, 51(5), 532–541. [doi:10.1057/palgrave.jors.2600941]
SQUAZZONI, F. (2012). Agent-Based Computational Sociology. Hoboken, NJ: John Wiley & Sons.
STATISTA. (2020a). Ad spend of selected insurance brands in the U.S. in 2019. Available at: https://www.statista.com/statistics/264968/ad-spend-of-selected-insurance-companies-in-the-us/.
SUTTON, R. S., & Barto, A. G. (2018). Reinforcement learning: An introduction. MIT press.
THE Society of Motor Manufacturers and Traders Limited. (2020). SMMT Motor Industry Facts 2020. Available at: smmt.co.uk/wp-content/uploads/sites/2/SMMT-Motor-Industry-Facts-JUNE-2020-FINAL.pdf.
TSOUKATOS, E., & Rand, G. K. (2006). Path analysis of perceived service quality, satisfaction and loyalty in greek insurance. Managing Service Quality: An International Journal, 16(5), 501–519. [doi:10.1108/09604520610686746]
ULBINAITE, A., & Le Moullec, Y. (2010). Towards an ABM-based framework for investigating consumer behaviour in the insurance industry. Economics, 89(2), 95–110.
WATTS, D. J., & Strogatz, S. H. (1998). Collective dynamics of “small-world” networks. Nature, 393(6684), 440–442. [doi:10.1038/30918]
ZHANG, R., Li, W., Tan, W., & Mo, T. (2017). Deep and shallow model for insurance churn prediction service. 2017 IEEE International Conference on Services Computing (SCC). [doi:10.1109/scc.2017.51]