Conflicting Information and Compliance with COVID-19 Behavioral Recommendations

, ,
and
Sandia National Laboratories, United States
Journal of Artificial
Societies and Social Simulation 25 (4) 6
<https://www.jasss.org/25/4/6.html>
DOI: 10.18564/jasss.4911
Received: 06-Dec-2021 Accepted: 11-Oct-2022 Published: 31-Oct-2022
Abstract
The prevalence of COVID-19 is shaped by behavioral responses to recommendations and warnings. Available information on the disease determines the population’s perception of danger and thus its behavior; this information changes dynamically, and different sources may report conflicting information. We study the feedback between disease, information, and stay-at-home behavior using a hybrid agent-based-system dynamics model that incorporates evolving trust in sources of information. We use this model to investigate how divergent reporting and conflicting information can alter the trajectory of a public health crisis. The model shows that divergent reporting not only alters disease prevalence over time, but also increases polarization of the population’s behaviors and trust in different sources of information.Introduction
The ultimate effects of the COVID-19 pandemic have been determined largely by human response to its spread (Chernozhukov et al. 2021; Zhang et al. 2021). As people learn about the danger and spread of the disease, they change their perceptions of risk and consequently their behavior; empirical studies have confirmed this phenomenon for COVID-19 (Kuper-Smith et al. 2021; Siegrist et al. 2021) as well as the impact of information on behavior more generally (Arias 2019; Dellavigna & Gentzkow 2010). Behavioral changes, such as compliance with stay-at-home orders, can affect the spread of the disease itself. This dynamic is further complicated by the fact that people do not have full information on which to make decisions and determine behavior. Media and social networks interpret and share imperfect and delayed information, while individuals consume subsets of available information and update both situational perceptions and their trust in the various sources of information (Jiang et al. 2021). Differential reactions to conflicting information can also cause polarization in beliefs, behaviors, and trust, leading to seemingly irrational behavior that can further alter disease dynamics.
Governments around the world have implemented different measures to encourage social distancing and other behaviors that reduce the spread of COVID-19 (Hale et al. 2021). Some of these governments, including many states in the U.S., implemented stay-at-home orders (Mervosh et al. 2020), which ask or require that citizens limit exposure to people and locations outside of their homes.
Even with stay-at-home orders in place, individuals make daily decisions about whether to leave their homes, for what reasons they should venture out, and what protective measures (such as using face masks) to take when they do. In addition, many governments with stay-at-home orders did not strictly enforce the orders as requirements and included a variety of exceptions. While specifics of the orders differed across states, essential workers were expected to continue going to work, and some activities that involve social contact, such as grocery shopping, were deemed acceptable for everyone. Early implementation of stay-at-home orders in the United States saw mixed results; the orders were somewhat effective at reducing movement and social interaction (Andersen 2020), but also met with resistance, both from citizens and from some state governments (Blake 2020). Phased re-openings further complicated decision making, with different economic sectors reopening at different times and with different restrictions. While guidance from the federal government has continued to encourage social distancing (CDC 2020), varying implementation of stay-at-home orders and differential compliance with those orders led to uneven social distancing within and among different communities.
In the United States, this differential compliance with stay-at-home orders was magnified by both culture and polarization. For example, the American tradition of individualism encourages resistance to large-scale government requirements, including compliance with stay-at-home orders. Similarly, America’s strong history of capitalism affects responses by emphasizing the importance of economic activity, and by encouraging cost-benefit analysis of different actions rather than straightforward compliance. Thus, while most Americans have supported restrictions related to COVID-19 (van Green & Tyson 2020), the timing and character of responses to stay-at-home orders and other COVID-19-related restrictions has been impacted by ideological polarization (Allcott et al. 2020). This polarized response has likely been exacerbated by divergent reporting from news sources (Bursztyn et al. 2020) that tend to connect with different portions of the population (Jurkowitz & Mitchell 2020), leading to subpopulations with markedly different information about the danger of the pandemic.
To capture the effects of this polarized information landscape, we developed a model of stay-at-home behavior, including compliance with stay-at-home orders. In this hybrid agent-based-system dynamics model, the perceived danger of COVID-19 affects individuals’ stay-at-home behavior and thus the spread of the disease, which goes on to affect perceived danger. Individuals learn of the dangers of the pandemic from news sources, and dynamically update their trust in those sources. They weigh their understanding of the danger of COVID-19 against economic and social motivations to leave home.
This model shows that polarization can emerge from divergent media reporting, even when those reports are based on similar information. Specifically, we incorporate social comparison theory (Festinger 1954), which states that individuals tend to adjust their opinions to assimilate with others, as long as the others opinions are similar enough to the individual’s opinion. If the others’ opinions are substantially different from the individual’s, however, the individual will tend to adjust their opinions to contrast with the others. We show that if media reporting on the danger of COVID-19 differs in timing and magnitude, substantial polarization in compliance with stay-at-home orders can emerge.
Understanding how psychology and information interact to affect individuals’ decisions about complying with stay-at-home orders is vital in managing the response to the COVID-19 pandemic. In order to determine the best ways to ease restrictions, and to re-implement restrictions should that become necessary, we must know how people react to these orders. The specific implementation of any such restrictions will affect compliance, as will other social and psychological factors. The model presented here simulates likely reactions to restrictions (and lifting of restrictions) related to the COVID-19 pandemic. This work contributes a new method for disease simulation that uses trust to model the inherent feedback dynamics between information, psychology, behavior, and disease. The model improves our understanding of the mechanisms driving how media and strategic health messaging can affect not only disease dynamics, but also polarization of the population and trust in information sources.
Related Research
In this work we focus on how strategic messaging and trust influence behavior, and integrate that information and behavioral feedback with classical disease modeling. Behavioral feedback has been explored using agent-based frameworks (Badham et al. 2018) with the coupling of fear and disease (Epstein et al. 2008) and inclusion of large scale behavioral adaptations (Del Valle et al. 2013), as well as on an individual level (Fenichel & Wang 2013). Media coverage and consequent human behavior has been shown to have significant impact on epidemic trajectories, even altering the fixed points on which the system operates (Cui et al. 2008; Fenichel et al. 2011). Within more classical models of epidemic spread, behavioral feedback can be introduced as a diffusive behavior (Poletti et al. 2013) or as a localized effect (Sun et al. 2011), but in either case shows a significant impact on the duration and persistence of the spread.
The COVID-19 pandemic, while still unfolding, has been the source of substantial recent effort in this field (Adam 2020; Lorig et al. 2021; Scientific Advisory Group For Emergencies 2021). There have been two main thrusts in this area; one to understand how the pandemic has unfolded through data collected empirically, and another to improve modeling with this data and utilize it to predict the pandemic dynamics. In the COVID-19 pandemic, the effect of social adaptations has become clear, especially in areas with official stay at home orders that showed a strong correlation between the orders and a reduction in both total cases and fatalities (Fowler et al. 2021).
This information has led to a shift in how classical epidemic models are considered; adding social influences has become much more common as increased accuracy begins to outweigh the drawbacks of increased complexity. Dynamic infection rates show promise in matching real-world effects (Shapiro et al. 2021), while more specific behavioral effects in the form of fear and frustration have increased accuracy in basic epidemiologic models (Johnston & Pell 2020; Perra et al. 2011; Rahmandad et al. 2021). Further studies into these effects have been represented in complex agent-based models that have been able to match specific empirical data sources by shifting and introducing new peaks in the systems (Barbarossa et al. 2020). These sorts of models allow for extremely fine grained control over the number and style of interventions considered, building complex models with high levels of accuracy that can predict peaks, timing, and are valuable in evaluating the trade-offs between the prevalence of the virus and the duration of the interventions implemented at the cost of high modeling complexity and specificity (Chang et al. 2020). Indeed, the exact nature of these tradeoffs has been evidenced by nonlinear feedback models that show oscillating dynamics with regard to social restrictions and disease prevalence that are robust to parameter variations (Pedro et al. 2020).
Mitigation strategies have also been investigated. Koehler et al. (2021) model the effects of interventions including stay-at-home orders, but rather than simulating behavior explicitly as demonstrated here, they assume a specified reduction in disease transmission probability. Badham et al. (2021) use simulation-backed justified stories to facilitate evaluation of policy alternatives related to COVID-19. Communication related to public health has also been investigated using agent-based modeling; Barbrook-Johnson et al. (2017) simulated the effects of government messaging on health-related behaviors, although without the dependence on repeated interaction and trust dynamics incorporated into the model presented here. Finally, hybrid modeling efforts have also gained prevalence in the COVID landscape, offering expanded compartmental models that include behavioral compartments and social exposure effects to control compartmental mixing (Bouchnita & Jebrane 2020; Zlojutro et al. 2019). These models often allow for decreased computational complexity over fine grained agent-based models while producing results that are still highly specific and predictive of data.
In contrast, our model focuses on how conflicting information affects behavioral responses to a public health crisis, and how those dynamics combine with disease prevalence itself to determine effects. The model utilizes a hybrid structure, with system dynamics (Ford 1999; Sterman 2000) determining behaviors and disease dynamics over time, and agent-based (Macal & North 2009) techniques driving social interactions. By combining the key factors of disease spread, information flow, and behavior, we believe that this model improves capabilities for simulating both disease dynamics and the consequences of information framing strategies over time.
Model
The model simulates the interplay between key influences on decisions about stay-at-home behavior, one example of preventative behaviors in general. The structure of the model is designed around two fundamental feedback loops (Figure 1). In the first, stay-at-home behavior affects the economy, and economic drivers influence the drive to leave home. In the second, behavior influences the spread and prevalence of COVID-19; individuals then learn about that prevalence and adjust their behavior accordingly. Thus, the model involves three overarching sectors: stay-at-home behavior is simulated using an agent-based concept with system dynamics-driven agent cognition, while economic and disease sectors use aggregated system dynamics model formulations. This structure was inspired by the theory of planned behavior (Ajzen 1991), which says that the three contributors to behavior determination are the (1) attitude toward the behavior, here interpreted as perception of danger, (2) subjective norms, here interpreted as the influence of the social network, and (3) perceived behavioral control, here interpreted as economic effects, in combination with the feedback structure between disease prevalence and behavior as exemplified by attempts to control disease spread through behavioral control policies.

A more detailed feedback structure of the model is shown in Figure 2, with the mathematics discussed below. The model focuses on three perceptual factors that influence individual decision making about whether and how much to stay home. The first input is the individual’s perceived social obligation to stay home, which is based on the decisions made by agents connected to the individual through the social network. The second input is the individual’s perceived danger of leaving home, which is influenced by the agent’s consumption of news messaging from the model’s two news sources. Each news source reports on actual rates of COVID-19 spread, but the two sources have different delays on reporting that information and different magnitudes of reported danger based on the data. As an agent hears reporting from a particular media source, it updates its perception of the danger of leaving home and updates its trust in the source of the message; media sources reporting danger that is substantially different from the agent’s current perception will lose trust, and vice versa. Finally, the agents’ stay-at-home behavior is influenced by a perceived need to leave home, which changes based on economic hardship exacerbated by the economic effects of large portions of the population staying home. As agents adjust their stay-at-home behavior, the economic situation and the spread of COVID-19 change accordingly.
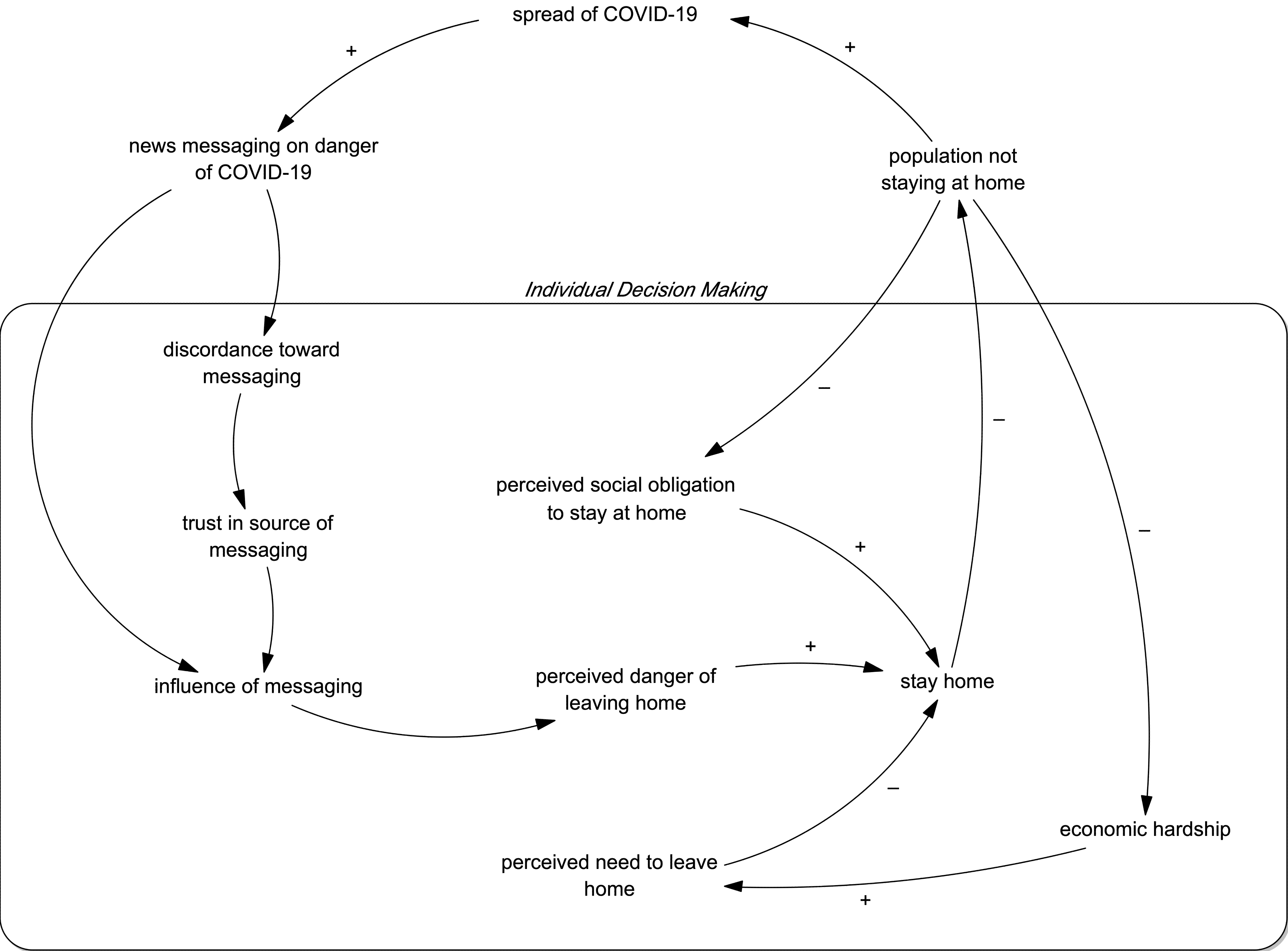
In our model, stay at home behavior results in a reduction in the spread of COVID-19. This dynamic can be considered representative of any number of the broad range of preventative behaviors relevant to pandemic response. However, we focus on stay at home as a synecdoche for the larger set since it has readily available data, is controlled on a large scale level, and has shown some effectiveness in disease mitigation (Brauner et al. 2021; Mingolla & Lu 2022).
We implemented the model in N2A software (Rothganger et al. 2014), a program originally designed for large-scale neuroscience simulations. Since the N2A modeling paradigm is domain-agnostic, it is equally useful for social-science simulations. N2A handles both agent-based and dynamical systems models, as well as hybrid models that combine the two paradigms. The N2A tool is open-source and available for zero cost from https://github.com/frothga/n2a.
All simulations start on January 1, 2020. The following subsections examine each sector of the model, including equations and calibration data, in more detail.
Stay-at-home behavior: Agent population
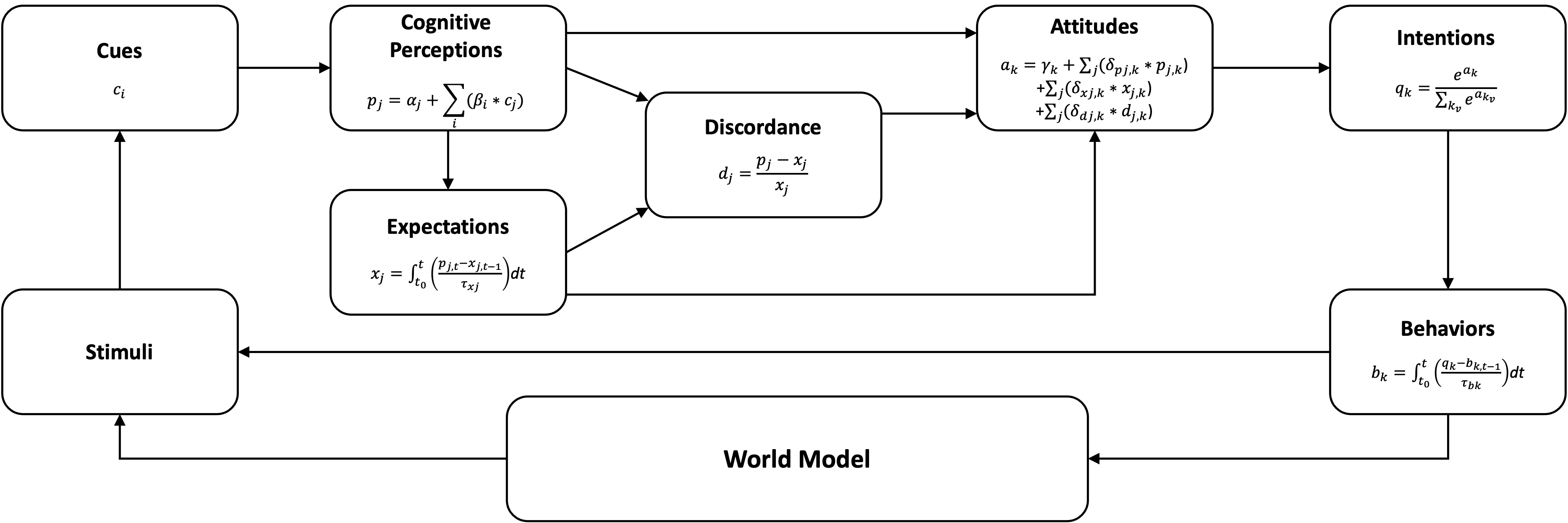
Each agent in the modeled population determines its stay-at-home behavior based on four input cues: information from news media (moderated by the agent’s trust in that media source), the behaviors of other agents in its social network, economic pressures, and stay-at-home orders implemented by the government. The cognitive model driving each agent is based on a modified version of the DYMATICA1 cognitive-system dynamics approach (Bernard et al. 2016) shown in Figure 3. The DYMATICA structure incorporates psychological, social, and economic theories, including prospect theory (Kahneman & Tversky 1979), qualitative choice theory (Mcfadden 1982), and the theory of planned behavior (Ajzen 1991), in a mathematically consistent and simulatable form. Detail on the design of the DYMATICA modeling structure is described by Bernard et al. (2016).
Agents in the model are exposed to cues, and interpret those cues using a weighted linear combination as cognitive perceptions. As cognitive perceptions change, they update the agent’s expectations, each modeled as a system dynamics stock with the associated cognitive perception as the only inflow, mediated by a time delay. The normalized difference between cognitive perceptions and expectations is the agent’s discordance. The agent combines cognitive perceptions, expectations, and discordance to determine its intention utility, or the benefit of taking of a particular action. In this application of the DYMATICA structure, the agents consider their perceptions of danger, need to leave home, and social obligation, as well as their discordance of danger and need to leave home, in determining their attitude toward staying home, the modeled behavior. Details on parameterization can be found in the Appendix and implemented model, available upon request. The agent then determines the magnitude of that intention using a multinomial logit function consistent with qualitative choice theory (Mcfadden 1982). The agents’ behaviors are lagged versions of their intentions. Actions feed into the larger world model, which simulates disease and economic dynamics, and can also serve as inputs to their own and others’ cognitive models in future time steps.
Agents interact with each other through a social network graph generated using the Newman-Watts-Strogatz algorithm (Newman & Watts 1999), as implemented in the NetworkX software package (Hagberg et al. 2008). The network is constant and the same network is used for all simulations. The results discussed here assume that the population contains 1000 agents, each with 10 direct neighbors and a 0.1 probability of connecting with distant agents.
Stay-at-home behavior: News sources
The modeled population’s perception of the danger of COVID-19 is influenced by two news source agents, both which report on the disease prevalence data but with different delays and magnitudes. News sources broadcast their information, and agents adjust their perceptions based on information from the news sources and their trust in those sources. Trust is dynamic, and adjusts according to the similarity between reporting and the agent’s current perceptions. The news sources use the DYMATICA cognitive-system dynamics structure described above. The two input cues are the number of detected COVID-19 cases and stay-at-home orders. The single behavioral output for each news source is the media source’s reporting on the danger of the pandemic.
While both news sources respond to the same information, they react to that information differently. Parameterization allows us to adjust both the magnitude and the time lag in reporting danger, discussed more below.
Stay-at-home behavior: Trust between population and news agents
The influence of a particular news source on an agent depends on the agent’s trust in that source. Trust is a dynamic factor, updating continuously as the agent receives information from the media source. If that information is consistent with the agent’s current understanding, trust in that news source increases, but if the information is unexpected the agent’s trust in the news source decreases.
Trust affects how the agent reacts to information broadcast by the media sources. Trust ranges from -1 to 1, and the magnitude of trust can be interpreted as the amount of attention the agent pays to the media source. When trust is positive, the agent considers the information as intended; for example, a higher value of reported danger will increase the agent’s proclivity to stay home. Negative trust causes the agent to take the contrary action. For example, if a media source in which the agent has negative trust reports more danger, the agent will defy the intended recommendation and leave home more. We initialize the population’s trust in the two news media sources based on data from Jurkowitz & Mitchell (2020).
Trust calculations (see Equations below) begin with the agent measuring the divergence between its expectations and reporting on the danger of the pandemic. Divergence is similar to discordance, but measures the absolute value of the difference rather than a normalized value. While discordance is measured in relation to the message recipient’s expectations, divergence is compared to the agent’s threshold. The agent then develops its indicated trust in the news source and interpretation of the new information. This dynamic trust metric adjusts as a system dynamics stock with a specified update lag, moderated by its loyalty to the news source. Loyalty is based on initial trust, modified by a \(loyaltyEffect\) parameter.
| \[ divergence = expectationOfDanger - reportedDanger\] | \[(1)\] |
| \[indicatedTrust = \begin{cases} if \; abs(divergence) < threshold: \; threshold - abs(divergence)/threshold\\ else: \; threshold - abs(divergence)/(1 - threshold) \end{cases}\] | \[(2)\] |
| \[ trust^{'} = (1 - loyalty)(indicatedTrust - trust)/lagTrust\] | \[(3)\] |
| \[ loyalty = loyaltyEffect \times max(initialTrust,0)\] | \[(4)\] |
Economic effects
The economic sector of the model involves a simple, aggregated system dynamics model based on a Cobb-Douglas production function.
| \[ production = technology \times capital^{\alpha} \times labor^{\beta}\] | \[(5)\] |
The labor input to this function adjusts from a baseline value based on the average stay-at-home behavior over the population of agents.
| \[ labor = baselineLabor \times (1 - averageStayHome \times baselineEmploymentRate)\] | \[(6)\] |
We use the production function to calculate the reduction in economic activity.
| \[ economyFractionReduced = (baselineProduction - production)/baselineProduction\] | \[(7)\] |
The population of agents all face the same perceived need to leave home, based on the reduction in economic activity as adjusting a baseline.
| \[ needToLeaveHome = baselineNeedToLeaveHome + economyFractionReduced\] | \[(8)\] |
Baseline production uses the same form as the equation for production, except an initial value of labor is incorporated.
| \[ baselineProduction = technology \times capital^{\alpha} \times initialLabor^{\beta}\] | \[(9)\] |
| \[ initialLabor = baselineLabor \times (1 - initStayHome \times baselineEmploymentRate)\] | \[(10)\] |
averageStayHome comes from the Stay-At-Home Behavior sector of the model. All model equations and parameters can be found in the Appendix.
Disease prevalence
We model the spread of COVID-19 using a modified version of a conventional compartmental SEIR (Susceptible, Exposed, Infectious, Recovered) epidemiological model (Figure 4). The key distinction in our model is the inclusion of a social distancing factor incorporated into the equation that governs the flow from Susceptible to Exposed.
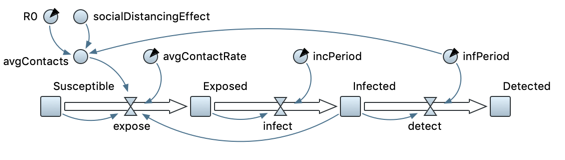
All compartments in our model are normalized, representing the fraction of the total population in each compartment. For simplicity we assume a constant population size. Stocks (Susceptible, Exposed, Infected, and Detected) are adjusted by flows as in a typical system dynamics model. Flows are calculated as:
| \[ expose = avgContacts \times Infected \times Susceptible\] | \[(11)\] |
| \[ infect = (1/incubationPeriod) \times Exposed\] | \[(12)\] |
| \[ detect = (1/infectiousPeriod) \times Infected\] | \[(13)\] |
The average contacts per day (\(avgContacts\)) is adjusted by a social distancing effect based on the Stay-at-Home Behavior sector of the model.
| \[ avgContacts = socialDistancingEffect \times R_{0} \times (1/infPeriod)\] | \[(14)\] |
| \[ socialDistancingEffect = 1 - avgStayHome \times socialDistancingMultiplier\] | \[(15)\] |
The model is initialized with the entire population in the Susceptible compartment, and a small percentage of the population is shifted to Infected at the start of the pandemic.
Model calibration
We calibrated the disease sector of the model based on COVID-19 cases for Miami-Dade County, Florida, USA (Florida Department of Health 2020), as well as population mobility data for the same location (Descartes LABS 2020). The data set includes reported cases and a mobility value indicating how far people travel in a day relative to the pre-pandemic period. Finally, that data set includes the date range for the Florida-wide stay-home order. To calibrate, we temporarily replaced avgStayHome with mobility data, and adjusted parameters (including cognitive parameters) to fit modeled cases to data in the first half of the simulation time horizon.
Calibration of the parameters in the economic sector of the model is based on unemployment data from Florida (U.S. Bureau Of Labor Statistics 2021) over the course of the model time horizon, and we use Okun’s law (Okun 1963) relating a percent increase in production to roughly half that percent decrease in unemployment rate to estimate the conversion of the unemployment data into production loss.
Results
We ran the model using a one-year time horizon, and calibrated it using data from Miami-Dade County, Florida. The primary feedback structure explored by the model is demonstrated in Figure 5, along with the stay-at-home order implemented by the government, which in Florida ran from April 1 through May 4, 2021. The model is initialized such that COVID-19 cases first appear on March 2, the day of the first detected case in Miami-Dade county. The population reacts to news about these cases and begins to increase how much they stay home as compared to baseline rates. In the early days of the disease, this reaction is based largely on discordance, or each agent’s discomfort with the new information; although the actual prevalence of the disease is still low, it is much higher than the population expects, causing a strong behavioral response. When the government implements a stay-at-home order, stay-at-home behavior increases sharply. This behavioral response reduces the average number of contacts, thus reducing the prevalence of COVID-19. When the stay-at-home order ends, the population reacts to both the order and a reduction in disease prevalence and sharply reduces its stay-at-home behavior. Disease rates begin to rise again. The population reacts to the increased danger after a short delay, increasing preventative behavior until disease rates drop again and the second wave of the disease ends. This process is cyclic; after another delay the population responds by leaving home more often and allowing the disease prevalence to increase, followed by another delayed increase in staying home.
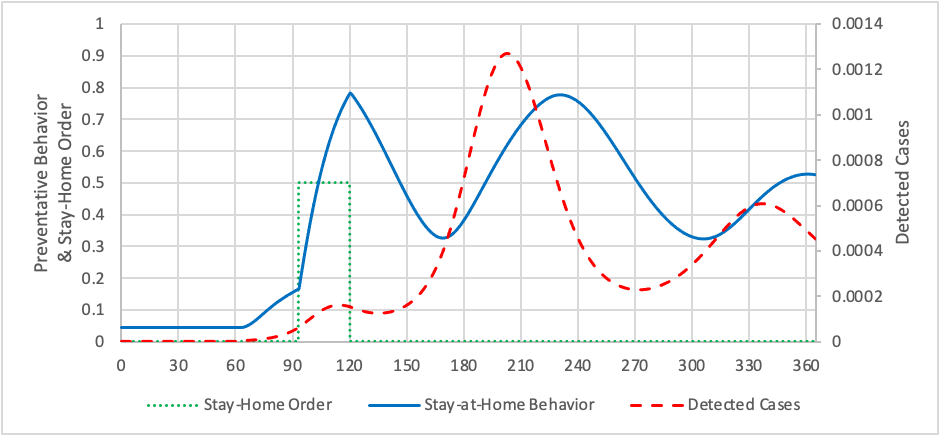
Figures 6 and 7 show simulation results compared to calibration data for detected cases and preventative behaviors respectively. The simulated detected cases show the three distinct waves of COVID-19 in its first year; goodness of fit for this calibration can be characterized by the mean absolute error normalized by the mean of the data (MAEN) is 36%. Preventative behaviors were more loosely calibrated to data, as no data source specifically on stay-home behavior was available. The data shown in Figure 7 is the inverse of mobility data (Descartes LABS 2020), and was considered a proxy for stay-home behavior. However, since this data only captured one aspect of that behavior, specifically changes in distance traveled, the model calibration was not targeted toward closely matching the dataset. However, we do find it to be a useful comparison, showing that this particular metric of preventative behavior did seem to peak early in the pandemic and coinciding with official stay-home orders. The inverse-of-mobility dataset does not exhibit the oscillations seen in the simulated preventative behavior. This might be explained by the exclusion from the model of other behavioral influences such as pandemic fatigue. Another likely explanation is that behavioral feedback with disease prevalence is influenced by a set of real-world behaviors that includes staying at home, but also includes a set of other behaviors such as mask wearing and social distancing.
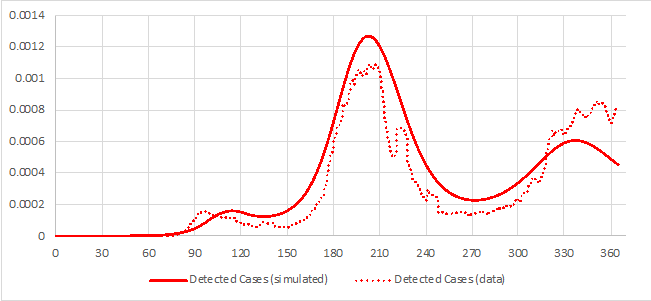
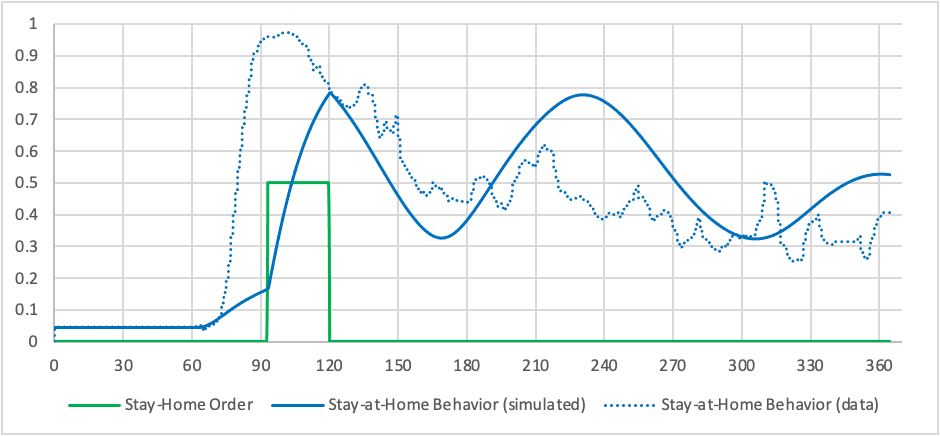
The population’s reaction to disease prevalence is filtered through two media sources, and each agent’s trust in those sources varies as messaging does (or does not) align with the current understanding of the agent. The magnitude of danger communicated by a media source, and particularly its difference from agents’ perspectives and from the other media sources, thus has a major effect on the agents’ perceive danger of the pandemic, and thus behavioral response and disease prevalence. Figures 8a and 8b compare preventative behaviors and disease prevalence for four scenarios: the base case which is based on actual reporting during the COVID-19 pandemic (Bursztyn et al. 2020), a low alarm scenario where both media sources report the same low level of danger, a high alarm scenario where media sources report the same high level of danger, and a divergent scenario where one media source reports very high alarm and the other reports very low alarm.
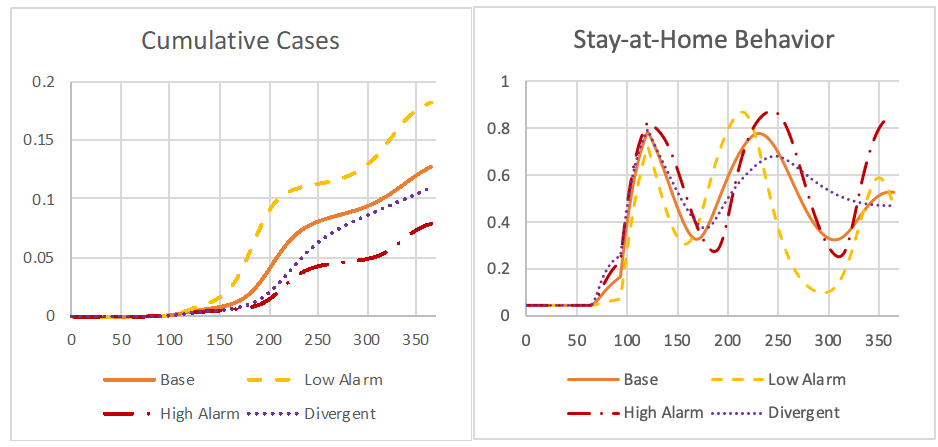
As expected, the most effective media strategy for reducing the number of cumulate cases of COVID-19 is for both media sources to consistently report a high level of alarm. Figure 9 gives further detail on all four scenarios. Both media sources respond to current disease prevalence in their reporting of COVID-19, but with differing magnitudes and delays. In the base case, News Source 1 reports substantially higher alarm than News Source 2. Agents’ initial trust in those news sources is chosen from a distribution. By the end of the base case simulation, the population’s range of trust in both sources narrows. The range of trust in Source 2, which reports lower alarm than Source 1, is wider and more polarized; the agents with the highest trust in a news source at the end of the simulation trust Source 2, but the agents with the lowest trust in a source also distrust Source 2. Source 1, which reported higher alarm, has a more consistent level of trust through the population. The base case also exhibits a wide range of preventative behaviors over the agent population. As the pandemic progresses, the range of behaviors expands, with some agents at near-maximum preventative behaviors and others taking nearly no preventative measures.
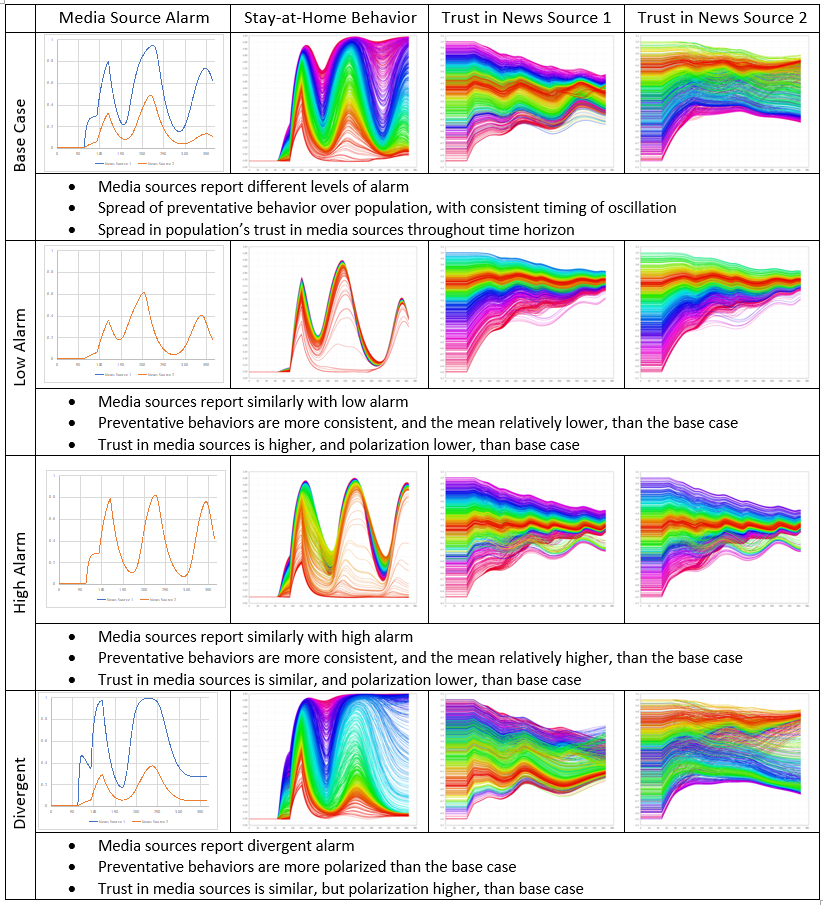
In the low alarm and high alarm cases, the two media sources are much more similar in their reporting. In the low alarm case, the media sources both respond to disease prevalence similarly to News Source 2 in the base case. Preventative behaviors over the population are much more consistent than in the base case; however, the magnitude of behavioral adjustment is lower for much of the population. Consistent but low reporting of alarm results in a much less polarized population, but, as seen in Figure 8a, the highest overall cumulative cases of COVID-19.
In the high alarm case, both media sources report similar levels of alarm as News Source 1 in the base case. When both media sources report high alarm, we see a relatively consistent and high level of preventative behavior (Figure 9), resulting in the lowest cumulative COVID-19 cases of any scenario (Figure 8a), the best outcome from the disease prevention perspective.
In both the low and high alarm cases, some portion of the population takes a contrarian position to reporting and does not implement preventative behaviors for some portion of the simulation. This phenomenon is seen more strongly in the high alarm case, as some people in the population do not adjust their expectations and trust in those sources quickly as the situation changes.
In all cases, trust initializes with a distribution across the population derived from Jurkowitz & Mitchell (2020). As the pandemic goes on, the trust model allows agents to update their trust, and thus their attention to a particular media source, based on the similarity of the media source’s messaging to the agent’s existing belief. The low alarm and high alarm cases both result in a narrower range of trust in the media sources as compared to the base case. Trust is similar for both media sources since they are reporting similarly, but with slight differences largely due to the initialization of the population’s trust in each source.
In the divergent case, the two news sources deviate somewhat more on their reporting of alarm than in the base case. The resulting number of cumulate COVID-19 cases (Figure 9) is similar but slightly lower than in the base case. A key characteristic of the divergent case is that it results in a more polarized population than any other case. The range of preventative behaviors is similar to the base case, but by the end of the simulation far more people are either very high or very low in their levels of preventative behaviors. The range of trust in media sources is the widest of any scenario, and trust in News Source 2 exhibits particularly strong polarization, with a large portion of the population having high trust in News Source 2 and another large portion of the population distrusting the source. While it was not explored in this model, this polarization can have further repercussions on the population, as the now-distinct groups may begin to distrust each other, which can contribute to further polarization (Adams et al. 2021).
Discussion
This model shows that negative feedback via human behavior is sufficient to explain much of the wave pattern of COVID-19 cases. Within the model, the progression of the pandemic is highly sensitive to the timing of human response. Without any negative feedback, infections might grow exponentially; understanding behavioral feedback, which this model demonstrates, may be crucial to predicting and influencing disease progression. Remarkably, such feedback is missing from standard compartmental models like SEIR, often leading to overestimations or the use of flat, artificial reductions in exposure rates. While behavioral feedback has been incorporated into some COVID models, the model presented here adds investigation of how that behavior depends on the how influencial information is produced and consumed, and attention, mediated by trust, changes dynamically with the information. This contributes to the modeling and simulation field’s response to the challenge of modeling human behavior related to COVID-19 (Squazzoni et al. 2020). Specifically, we add consideration of information complexity to COVID behavioral modeling, and facilitate exploration of public health messaging policies when information sources conflict.
The trust model described here can be used to explore the open question of whether it is better in public health messages to report the worst-case scenario that SEIR predicts or to give a more realistic projection. The more dire message might produce more fear and therefore more preventative behavior. However, when the predictions fail to come true, the public may lose trust in the source of the messages, which could damage outcomes in the long run.
Another perspective on how public health messaging interacts with the behavior-disease feedback system comes from control theory. Behavior in this case can be viewed as the output seeking a policy that dampens the oscillations in disease prevalence. Control theory is primarily used in industrial control systems, but has been applied to social systems simulated with system dynamics models (for example: Saeed 2008; Paine 2022). In simple terms, if the case rate is getting worse, agents perceive more danger and increase preventative behaviors. Likewise, if cases (and thus perceived danger) decreases, the agents relax and reduce preventative behavior. Public health messaging policy might compensate for this to reduce oscillations in new cases by emphasizing danger even when case rates drop. However, if the messaging is counter-intuitive when compared to case data, trust in the source of danger messaging may drop. Models such as this one can be useful in balancing short term influence against long term trust.
In our model (and in the US generally) news sources work independent of government policy and not necessarily beholden to public health messaging strategies; instead, the news sources pass along their interpretations of health data to the agent population. News sources thus play a crucial role in this system, and the model suggests that focusing attention on particular news sources can literally be a life-or-death choice. Still, inclusion of a direct source government agent would be a worthwhile addition to such a model; although this agent would not necessarily present the pure ground truth it could be general source of information and represent an important layer of delay and interpretation in the chain of information.
Conclusions
Human behavior will determine the ultimate effects of the COVID-19 pandemic and other public health crises, and methods for simulating and predicting those effects can help us to manage current and future events (Squazzoni et al. 2020). This article focuses on preventative behaviors such as stay-home orders, but the principles also apply to vaccination decisions and other behavioral responses. The level of alarm reported by news media can determine behavioral responses, but these responses also depend on how quickly people update their expectations and trust in sources on information. If information changes too quickly, contrarian responses may increase. Eventually, contradictory reporting among news sources can lead to polarization; while some news sources may have incentives to promote polarization, overall impacts on public health and other social dynamics can be detrimental.
Further, public health experts must balance the short- and long-term effects of their communications. Recommendations that exaggerate or misrepresent a threat might improve public health in the short term, but at the expense of public trust. This balance is complicated by the causal feedback between disease and behavior; if early warnings are effective, long-term disease rates are likely to be lower due to behavioral modification. People may notice that long-term trends do not match warnings from public health professionals and lose trust in those information sources. Messaging that leads to high agent discordance, with warnings far out of line with the population’s expectations, may be the most memorable and thus the most damaging to trust over time.
To compound these difficulties, the messages are spread through media sources and social networks with their own evolving understanding of the situation, so that different sectors of the population access different combinations of conflicting information. The population’s interpretation of the information to which they are exposed, and their subsequent change in behavior and trust in information sources, is heavily influenced by cultural responses to authority. Because of these difficulties, feedback structures, and short- and long-term effects, models such as the one introduced here are important in developing risk communication strategies that are likely to be interpreted well by the target population and reduce the risk of lost trust.
Governmental actions and societal reactions control how the virus spreads, which determines the speed and magnitude of the crisis’ impact on health, the world economy, and a huge number of other second and higher order effects. The trust dynamic model introduced here has potential to improve our understanding and forecasting of a critical set of national security threats that involve how people interpret conflicting information. Disinformation campaigns and the spread of false or misleading information as misinformation threatens stability, introduces extremism, and intensifies national security threats such as health crises. Relatedly, governments and others use strategic communications and information warfare to influence and manipulate target groups. These threats have escalated in recent years due to the growth in speed of communication introduced by the internet and social media. Understanding how people interpret and react to information from different sources is critical in managing these changing threats. The trust dynamic model introduced in this article interprets psychological understanding into a mathematical model that facilitates research into how psychology and information flow combine to influence social systems.
Acknowledgements
Sandia National Laboratories is a multimission laboratory managed and operated by National Technology & Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International Inc., for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-NA0003525. The content of the information does not necessarily reflect the position or the policy of the Government, and no official endorsement should be inferred.Notes
Appendix: Model Pseudo-Code
The pseudo-code below describes the structure of the model and parameter values for the base case scenario. We list these equations with long-form variable names for clarity. Derivatives with respect to time (\(d/dt\)) are noted with a prime mark (\('\)) after the variable name. Other variables may also vary over time as a consequence of having inputs that vary, but these are updated directly on each simulation time step rather than using derivatives.
Economic effects
\(production = technology \times capital^{\alpha} \times labor^{\beta}\)
\(labor = baselineLabor \times (1 - averageStayHome \times baselineEmploymentRate)\)
\(baselineProduction = technology \times capital^{\alpha} \times initialLabor^{\beta}\)
\(initialLabor = baselineLabor \times (1 - initStayHome \times baselineEmploymentRate)\)
\(economyFractionReduced = (baselineProduction - production)/baselineProduction\)
\(needToLeaveHome = baselineNeedToLeaveHome + economyFractionReduced\)
\(\alpha = 0.403\)
\(\beta = 1.094\)
\(baselineNeedToLeaveHome = 0.608\)
\(baselineEmploymentRate = 0.6\)
\(baselineLabor = 157919.23\)
\(capital = 514.94\)
\(technology = 0.0031\)
Disease prevalence
\(Susceptible^{’} = - exposureRate\)
\(Exposed^{’} = exposureRate - Exposed / IncubationPeriod\)
\(Infectious^{’} = Exposed / IncubationPeriod - Infectious / InfectiousPeriod\)
\(Recovered^{’} = Infectious / InfectiousPeriod\)
\(exposureRate = socialDistancingEffect \times R_{0} \times Susceptible \times Infectious / InfectiousPeriod\)
\(socialDistancingEffect = 1 - avgStayHome \times socialDistancingMultiplier\)
\(IncubationPeriod = 8d\)
\(InfectiousPeriod = 3d\)
\(R_{0} = 2.57\)
\(socialDistancingMultiplier = 0.86\)
General DYMATICA model
\(C\) = vector of Cues
\(W\) = matrix of weights between Cues and Perceptions
\(P = WC\) = vector of Perceptions
\(E\) = vector of Expectations
\(E^{'} = max(0, P-E)/tauLearn - max(0, E-P)/tauForget\), where \(/\) is elementwise division
\(D = tanh((P-E)/E)\) = vector of Discordances
\([P;E;D]\) = column vector where \(P\), \(E\) and \(D\) are stacked vertically
\(Α\) = matrix of weights between \([P;E;D]\) and Utilities
\(\Gamma\) = vector of constant inputs to Utilities
\(U = A[P;E;D] + \Gamma\) = vector of Utilities
\(actions = exp(U)/sum(exp(U))\)
News agent (DYMATICA, 2 instances)
\(C = [Recovered^{’}/DetectionRatio; SHO]\)
\(W = 2 \times 2\) identity matrix, such that \(P=C\)
News Source 1
\(tauLearn = [7d; 28d]\)
\(tauForget = [7d; 28d]\)
\(A = [1e4, 15, 0, 0, 6, 0]\)
News Source 2
\(tauLearn = [14d; 28d]\)
\(tauForget = [14d; 28d]\)
\(A = [0.5e4, 7, 0, 0, 3, 0]\)
\(SHO\) – Time series collected for region under study. Starts at 0. On day of stay-home order (day 93) it jumps to 1. On day that order ends (120) it returns to 0
\(DetectionRatio = 3\)
Human agent (DYMATICA, 1000 instances)
\(C = [danger; \; stay-home \; order; \; social \; obligation; \; needToLeaveHome]\)
\(W = 4 \times 4\) identity matrix, such that \(P=C\)
\(tauLearn = [14d; 28d; 40d; 28d]\)
\(tauForget = [14d; 28d; 40d; 28d]\)
\(U = [stay \; home; \; don’t \; stay \; home]\)
| \[A = \begin{pmatrix}10, 5, 0.5, 0,&0, 0, 0, 0,&0.5, 0, 0, 0\\ 0, 0, 0, 1,&0, 0, 0, 0,&0, 0, 0, 0,\end{pmatrix}\] |
Group = assigned by random draw, based on statistics for region under study
Trust (edge between Human agent and News agent)
\(diff = E(danger) - alarm\)
indicatedTrust =
if abs(diff) < thresholdTrust: thresholdTrust - abs(diff)/thresholdTrust
else: thresholdTrust - abs(diff)/(1 - thresholdTrust)
interpretation =
if diff < 0: 1 - E(danger)
else: E(danger)\(trust^{'} = (1 - loyalty \times loyaltyEffect) \times (indicatedTrust - trust)/tauTrust\)
\(loyaltyEffect = 0.5\)
\(tauTrust = 120d\)
\(initialTrust = Gaussian(mean(group, news \; source), deviation(group, news \; source))\)
\(loyalty = max(initialTrust,0)\)
\(thresholdTrust = 0.2\)
References
ADAM, D. (2020). The simulations driving the world’s response to COVID-19. Nature, 580, 316–318.
ADAMS, J., White, G., & Araujo, R. (2021). The role of mistrust in the modelling of opinion adoption. Journal of Artificial Societies and Social Simulation, 24(4), 4: https://www.jasss.org/24/4/4.html.
AJZEN, I. (1991). The theory of planned behavior. Organizational Behavior and Human Decision Processes, 50, 179–211.
ALLCOTT, H., Boxell, L., Conway, J., Gentzkow, M., Thaler, M., & Yang, D. (2020). Polarization and public health: Partisan differences in social distancing during the coronavirus pandemic. Journal of Public Economics, 191, 104254.
ANDERSEN, M. (2020). Early evidence on social distancing in response to COVID-19 in the United States. Available at: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3569368.
ARIAS, E. (2019). How does media influence social norms? Experimental evidence on the role of common knowledge. Political Science Research and Methods, 7(3), 561–578.
BADHAM, J., Barbrook-Johnson, P., Caiado, C., & Castellani, B. (2021). Justified stories with agent-based modelling for local COVID-19 planning. Journal of Artificial Societies and Social Simulation, 24(1), 8: https://www.jasss.org/24/1/8.html.
BADHAM, J., Chattoe-Brown, E., Gilbert, N., Chalabi, Z., Kee, F., & Hunter, R. F. (2018). Developing agent-based models of complex health behaviour. Health & Place, 54, 170–177.
BARBAROSSA, M. V., Fuhrmann, J., Meinke, J. H., Krieg, S., Varma, H. V., Castelletti, N., & Lippert, T. (2020). Modeling the spread of COVID-19 in Germany: Early assessment and possible scenarios. PLoS One, 15(9), e0238559.
BARBROOK-JOHNSON, P., Badham, J., & Gilbert, N. (2017). Uses of agent-based modeling for health communication: The TELL ME case study. Health Communication, 32(8), 939–944.
BERNARD, M. L., Backus, G. A., Naugle, A. B., Jeffers, R. F., & Damron, R. W. (2016). 'Modeling sociocultural influences on decision making: Assessing conflict and stability.' In J. V. Cohn, S. Schatz, H. Freeman, & D. J. Y. Combs (Eds.), Modeling Sociocultural Influences on Decision Making: Understanding Conflict, Enabling Stability (pp. 449–472). Boca Raton, FL: CRC Press.
BLAKE, A. (2020). A timeline of Trump playing down the coronavirus threat.
BOUCHNITA, A., & Jebrane, A. (2020). A hybrid multi-scale model of COVID-19 transmission dynamics to assess the potential of non-pharmaceutical interventions. Chaos, Solitons & Fractals, 138, 10994.
BRAUNER, J. M., Mindermann, S., Sharma, M., Johnston, D., Salvatier, J., Gavenčiak, T., Stephenson, A. B., Leech, G., Altman, G., Mikulik, V., Norman, A. J., Monrad, J. T., Besiroglu, T., Ge, H., Hartwick, M. A., The, Y. W., Chindelevitch, L., Gal, Y., & Kulveit, J. (2021). Inferring the effectiveness of government interventions against COVID-19. Science, 371(6531).
BURSZTYN, L., Rao, A., Roth, C. P., & Yanagizawa-Drott, D. H. (2020). Misinformation during a pandemic. National Bureau of Economic Research, Working Paper No. w27417.
CDC. (2020). Summary of Guidance for Public Health Strategies to Address High Levels of Community Transmission of SARS-CoV-2 and Related Deaths, December 2020. Available at: https://www.cdc.gov/mmwr/volumes/69/wr/mm6949e2.htm.
CHANG, S. L., Harding, N., Zachreson, C., Cliff, O. M., & Prokopenko, M. (2020). Modelling transmission and control of the COVID-19 pandemic in Australia. Nature Communications, 11(1), 1–13.
CHERNOZHUKOV, V., Kasahara, H., & Schrimpf, P. (2021). Causal impact of masks, policies, behavior on early Covid-19 pandemic in the US. Journal of Econometrics, 220(1), 23–62.
CUI, J. A., Tao, X., & Zhu, H. (2008). A SIS infection model incorporating media coverage. The Rocky Mountain Journal of Mathematics, 1323–1334.
DELLAVIGNA, S., & Gentzkow, M. (2010). Persuasion: Empirical evidence. Annual Review of Economics, 2(1), 643–669.
DEL Valle, S. Y., Mniszewski, S. M., & Hyman, J. M. (2013). 'Modeling the impact of behavior changes on the spread of pandemic influenza.' In P. Manfredi & A. D’Onofrio (Eds.), Modeling the Interplay Between Human Behavior and the Spread of Infectious Diseases (pp. 59–77). New York, NY: Springer.
DESCARTES LABS. (2020). Data for mobility changes in response to COVID-19. Retrieved December 7, 2020, from: https://github.com/descarteslabs/DL-COVID-19.
EPSTEIN, J. M., Parker, J., Cummings, D., & Hammond, R. A. (2008). Coupled contagion dynamics of fear and disease: Mathematical and computational explorations. PLoS One, 3(12), e3955.
FENICHEL, E. P., Castillo-Chavez, C., Ceddia, M. G., Chowell, G., Parra, P. A. G., Hickling, G. J., Holloway, G., Horan, R., Morin, B., Perrings, C., Springborn, M., Velazquez, L., & Villalobos, C. (2011). Adaptive human behavior in epidemiological models. Proceedings of the National Academy of Sciences, 108(15), 6306–6311.
FENICHEL, E. P., & Wang, X. (2013). 'The mechanism and phenomena of adaptive human behavior during an epidemic and the role of information.' In P. Manfredi & A. D’Onofrio (Eds.), Modeling the Interplay Between Human Behavior and the Spread of Infectious Diseases (pp. 153–168). New York, NY: Springer.
FESTINGER, L. (1954). A theory of social comparison processes. Human Relations, 7(4), 117–140.
FLORIDA Department of Health. (2020). Florida COVID 19 cases by day for time series. Retrieved December 7, 2020, from: https://open-fdoh.hub.arcgis.com/datasets/452ab45aaa714042b3d61c741f851d5a_0/data.
FORD, F. A. (1999). Modeling the Environment: An Introduction to System Dynamics Models of Environmental Systems. Washington, DC: Island Press.
FOWLER, J. H., Hill, S. J., Levin, R., & Obradovich, N. (2021). Stay-at-home orders associate with subsequent decreases in COVID-19 cases and fatalities in the United States. PLoS One, 16(6), e0248849.
HAGBERG, A. A., Schult, D. A., & Swart, P. J. (2008). Exploring network structure, dynamics, and function using NetworkX. Proceedings of the 7th Python in Science Conference (SciPy2008).
HALE, T., Angrist, N., Goldszmidt, R., Kira, B., Petherick, A., Phillips, T., Webster, S., Cameron-Blake, E., Hallas, L., Majumdar, S., & Tatlow, H. (2021). A global panel database of pandemic policies (Oxford COVID-19 Government Response Tracker). Nature Human Behaviour, 5(4), 529–538.
JIANG, X., Hwang, J., Shah, D. V., Ghosh, S., & Brauer, M. (2021). News attention and social-Distancing behavior amid COVID-19: How media trust and social norms moderate a mediated relationship. Health Communication, 37(1), 1–10.
JOHNSTON, M. D., & Pell, B. (2020). A dynamical framework for modeling fear of infection and frustration with social distancing in COVID-19 spread. Mathematical Biosciences and Engineering, 17(6), 7892–7915.
JURKOWITZ, M., & Mitchell, A. (2020). Cable TV and COVID-19: How Americans perceive the outbreak and view media coverage differ by main news source. Retrieved December 7, 2020, from: https://www.journalism.org/2020/04/01/cable-tv-and-covid-19-how-americans-perceive-the-outbreak-and-view-media-coverage-differ-by-main-news-source/.
KAHNEMAN, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 1, 263–291.
KOEHLER, M., Slater, D. M., Jacyna, G., & Thompson, J. R. (2021). Modeling COVID-19 for lifting non-pharmaceutical interventions. Journal of Artificial Societies and Social Simulation, 24(2), 9: https://www.jasss.org/24/2/9.html.
KUPER-SMITH, B. J., Doppelhofer, L. M., Oganian, Y., Rosenblau, G., & Korn, C. W. (2021). Risk perception and optimism during the early stages of the COVID-19 pandemic. Royal Society Open Science, 8(11), 1–21.
LORIG, F., Johansson, E., & Davidsson, P. (2021). Agent-based social simulation of the Covid-19 pandemic: A systematic review. Journal of Artificial Societies and Social Simulation, 24(3), 5: https://www.jasss.org/24/3/5.html.
MACAL, C. M., & North, M. J. (2009). Agent-based modeling and simulation. Proceedings of the IEEE 2009 Winter Simulation Conference (WSC).
MCFADDEN, D. (1982). 'Qualitative response models.' In W. Hildenbrand (Ed.), Advances in Econometrics. Cambridge: Cambridge University Press.
MERVOSH, S., Lu, D., & Swales, V. (2020). See which States and cities have told residents to stay at home. New York Times. Available at: https://www.nytimes.com/interactive/2020/us/coronavirus-stay-at-home-order.html.
MINGOLLA, S., & Lu, Z. (2022). Impact of implementation timing on the effectiveness of stay-at-Home requirement under the COVID-19 pandemic: Lessons from the Italian case. Health Policy, In press.
NEWMAN, M. E., & Watts, D. J. (1999). Renormalization group analysis of the small-world network model. Physics Letters A, 263(4–6), 341–346.
OKUN, A. M. (1963). Potential GNP: Its measurement and significance. Cowles Foundation for Research in Economics at Yale University.
PAINE, J. (2022). Applying an endogenized PID controller design to speculative bubble. Available at: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4137800.
PEDRO, S. A., Ndjomatchoua, F. T., Jentsch, P., Tcheunche, J. M., Anand, M., & Bauch, C. T. (2020). Conditions for a second wave of COVID-19 due to interactions between disease dynamics and social processes. Frontiers in Physics, 8.
PERRA, N., Balcan, D., Gonçalves, B., & Vespignani, A. (2011). Towards a characterization of behavior-disease models. PloS One, 6(8), e23084.
POLETTI, P., Caprile, B., Ajelli, M., & Merler, S. (2013). 'Uncoordinated human responses during epidemic outbreaks.' In P. Manfredi & A. D’Onofrio (Eds.), Modeling the Interplay Between Human Behavior and the Spread of Infectious Diseases (pp. 79–91). New York, NY: Springer.
RAHMANDAD, H., Lim, T. Y., & Sterman, J. (2021). Behavioral dynamics of COVID-19: Estimating underreporting, multiple waves, and adherence fatigue across 92 nations. Systems Dynamics Review, 37(1), 5–31.
ROTHGANGER, F., Warrender, C., Trumbo, D., & Aimone, J. B. (2014). N2A: A computational tool for modeling from neurons to algorithms. Frontiers in Neural Circuits, 8.
SAEED, K. (2008). Trend forecasting for stability in supply chains. Journal of Business Research, 61(11), 1113–1124.
SCIENTIFIC Advisory Group For Emergencies. (2021). SPI-M-O: Summary of modelling for scenarios for COVID-19 autumn and winter 2021 to 2022. Retrieved July 14, 2022, from: https://www.gov.uk/government/publications/spi-m-o-summary-of-modelling-for-scenarios-for-covid-19-autumn-and-winter-2021-to-2022-13-october-2021.
SHAPIRO, M. B., Karim, F., Muscioni, G., & Augustine, A. S. (2021). Adaptive susceptible-Infectious-Removed model for continuous estimation of the COVID-19 infection rate and reproduction number in the United States: Modeling study. Journal of Medical Internet Research, 23(4), e24389.
SIEGRIST, M., Luchsinger, L., & Bearth, A. (2021). The impact of trust and risk perception on the acceptance of measures to reduce COVID‐19 cases. Risk Analysis, 41(5), 787–800.
SQUAZZONI, F., Polhill, J. G., Edmonds, B., Ahrweiler, P., Antosz, P., Scholz, G., Chappin, E., Borit, M., Verhagen, H., Giardini, F., & Gilbert, N. (2020). Computational models that matter during a global pandemic outbreak: A call to action. Journal of Artificial Societies and Social Simulation, 23(2), 10: https://www.jasss.org/24/2/10.html.
STERMAN, J. (2000). Business Dynamics. New York, NY: McGraw-Hill.
SUN, C., Yang, W., Arino, J., & Khan, K. (2011). Effect of media-induced social distancing on disease transmission in a two patch setting. Mathematical Biosciences, 230(2), 87–95.
U.S. Bureau Of Labor Statistics. (2021). Labor force statistics from the current population survey. Retrieved June 3, 2021, from: https://beta.bls.gov/dataViewer/view/timeseries/LNS12300000.
VAN Green, T., & Tyson, A. (2020). 5 facts about partisan reactions to COVID-19 in the U.S. Pew Research Center. Available at: pewresearch.org/fact-tank/2020/04/02/5-facts-about-partisan-reactions-to-covid-19-in-the-u-s/.
ZHANG, N., Jia, W., Lei, H., Wang, P., Zhao, P., Guo, Y., Dung, C., Bu, Z., Xue, P., Xie, J., ZHANG, Y., Cheng, R., & Li, Y. (2021). Effects of human behavior changes during the coronavirus disease 2019 (COVID-19) pandemic on influenza spread in Hong Kong. Clinical Infectious Diseases, 73(5), 1142–1150.
ZLOJUTRO, A., Rey, D., & Gardner, L. (2019). A decision-support framework to optimize border control for global outbreak mitigation. Scientific Reports, 9(1), 1–14.