Dietrich Stauffer, Adriano Sousa and Christian Schulze (2004)

Discretized Opinion Dynamics of The Deffuant Model on Scale-Free Networks

Journal of Artificial Societies and Social Simulation vol. 7, no. 3
<https://www.jasss.org/7/3/7.html>

To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary

Received: 23-Oct-2003    Accepted: 23-Mar-2004    Published: 30-Jun-2004

Abstract

The consensus model of Deffuant et al is simplified by allowing for many discrete instead of infinitely many continuous opinions, on a directed Barabási-Albert network. A simple scaling law is observed. We then introduce noise and also use a more realistic network and compare the results. Finally, we look at a multi-layer model representing various age levels, and we include advertising effects.

Keywords:

Monte Carlo, Sociophysics, Consensus

Introduction

1.1

Computer simulation of opinion dynamics (consensus models) (Axelrod 1997; Deffuant 2000; Deffuant 2002; Weisbuch 2002; Hegselmann 2002; Hegselmann 2004; Krause 1997; Sznajd-Weron 2000; Stauffer 2000; Stauffer 2002; Galam 1990; Galam 1997; Stauffer 2003) is an important part of sociophysics (Weidlich 2000; Moss de Oliveira 1999; Schweitzer 2003). One checks if, starting from a random distribution of opinions (Monte Carlo method), one ends up with a consensus or a diversity of final opinions. The simulated people (”agents”) are located on lattices, on scale-free networks (Albert 2002; Barabási 2002), or form a purely topological structure where everybody can be connected with everybody. For the particular case of the consensus model of Deffuant et al (Deffuant 2000; Deffuant 2002; Weisbuch 2002), it was shown that on a Barabási-Albert (BA) network (Stauffer 2004) (see also Weisbuch 2004) the number S of different surviving opinions (if no complete consensus was achieved) was an extensive quantity, i.e. it varied proportional to the number N of agents, while it is intensive (independent of N for large N) when everybody can be connected to everybody (Ben-Naim 2003). The literature on Barabási-Albert networks contains many comparisons with reality, e.g. for the computer networks of the Internet.

1.2

The motivation of the present work is two-fold: We want to have an unambiguous criterion whether two opinions agree or disagree, and thus use discrete instead of continuous variables for the opinions, section 2. Then we want to make the model more realistic by introducing noise representing events outside the opinion dynamics of Deffuant et al, by using in section 3 a more realistic network (Davidsen 2002; Holme 2002; Szabó 2003) with a higher clustering coefficient that the BA network, by allowing for advertising through mass media, and by taking into account more than one layer in order to implement an age structure; the last two effects are dealt with in section 4. An appendix gives the basic Fortran program.

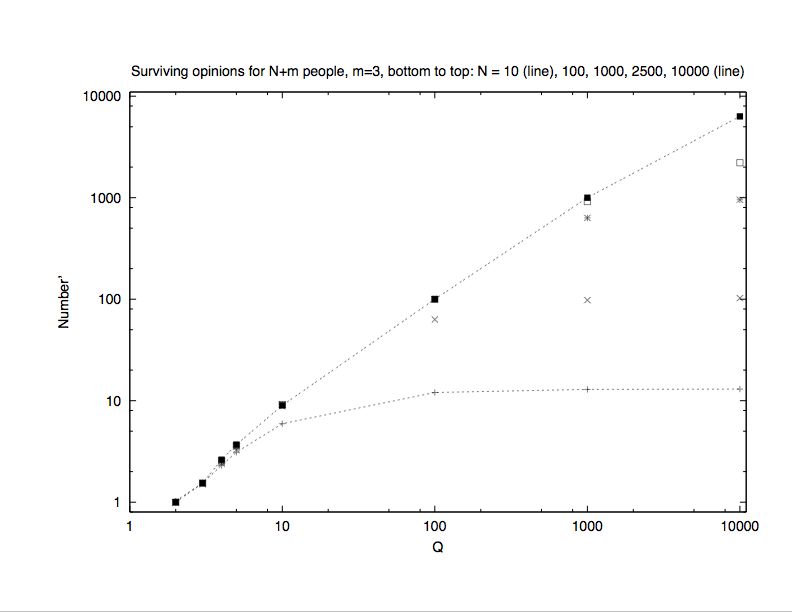
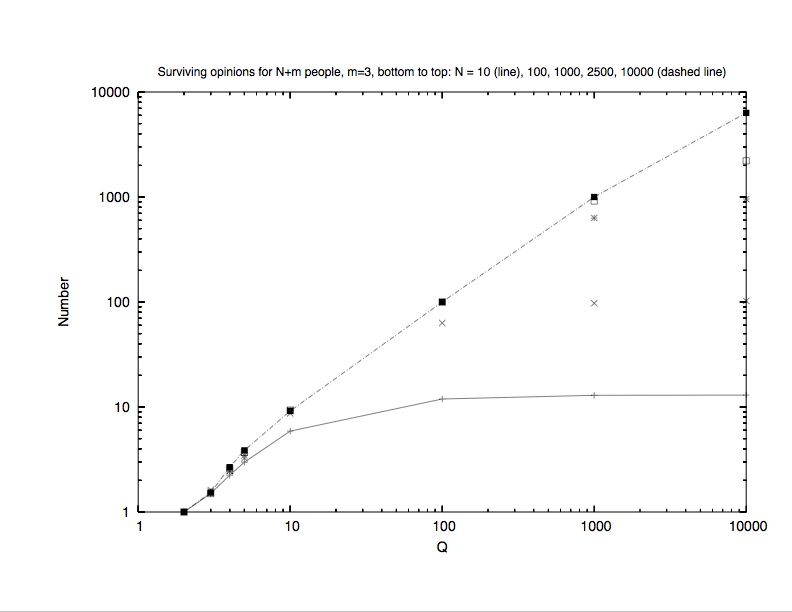
Figure 1. Number of different surviving opinions versus total number Q of opinions, for various network sizes N. Data for N = 10 and N = 105 are connected by lines.

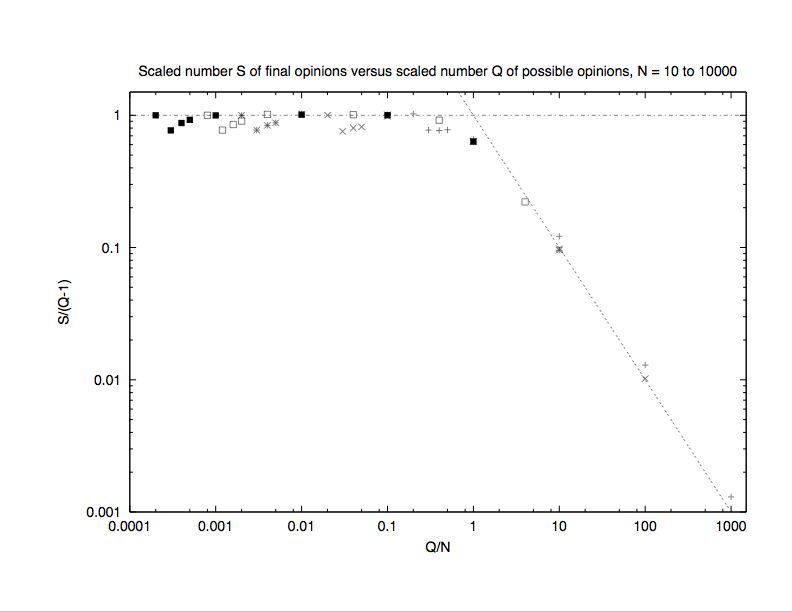
Figure 2. Scaled plot of the same data as in Fig.1. The straight lines indicate the ”trivial” scaling limit: Everybody keeps its own opinion in the right part, and each opinion is shared by many in the left part.

Basic model and noise

2.1

Instead of allowing for the opinions any real number between 0 and 1, we take them as discrete numbers q = 1, 2,...Q, as in the Sznajd model (Sznajd-Weron 2000; Stauffer 2000; Stauffer 2002). Now it is well defined if two opinions differ or agree, while for real numbers it depends on the accuracy of the simulation. At first, only people differing by ±1 in their opinion can convince each other (bounded confidence (Hegselmann 2002; Hegselmann 2004; Krause 1997, Deffuant 2000; Deffuant 2002; Weisbuch 2002)); thus 1/Q corresponds to the confidence interval of the previous models. If two agents with opinions differing by one unit talk to each other, randomly one of them takes the opinion of the other (Axelrod 1997). We put agents on a directed Barabási-Albert (Albert 2002; Barabási 2002; Stauffer 2004) network, starting with m = 3 agents connected with each other and with themselves; thereafter, N agents are added, each of which selects m pre-existing agents to be connected with. These randomly selected old agents are not regarded as connected to the new agent, i.e. the connections are directed. In this BA network the number of agents having k neighbours is known to be proportional to 1/k³. The size of the network is the number N of agents on it, i.e. the population.

2.2

First we construct the network, then we start the opinion dynamics from a random distribution of opinions. For each iteration we go through all agents in the order in which they were added to the network, and each selects randomly one of the m agents it had chosen before to be connected with. The simulation stops if no agent changed opinion during one iteration. (About the same results are obtained from random instead of regular updating, provided we stop if for ten consecutive iterations no opinion changed.)

2.3

Figure 1 shows that for large N the number S of surviving final opinions roughly equals Q for not too small Q; for Q = 2, on the other hand, nearly always a complete consensus S = 1 was found. (We averaged over 1000 samples except for N = 10⁵ when only 100 samples were used.) If, however, Q grows to values closer to N, then the finite size of the network is felt: S is lower than Q and approaches N + m, that means everybody keeps its own opinion and the simulation stops soon. A finite-size scaling formula fits reasonably the same data, Figuse 2, except for small Q. Thus, the number S of final opinions is an extensive quantity if Q is varied as N, and it is an intensive quantity if Q is kept constant when N . 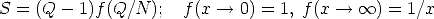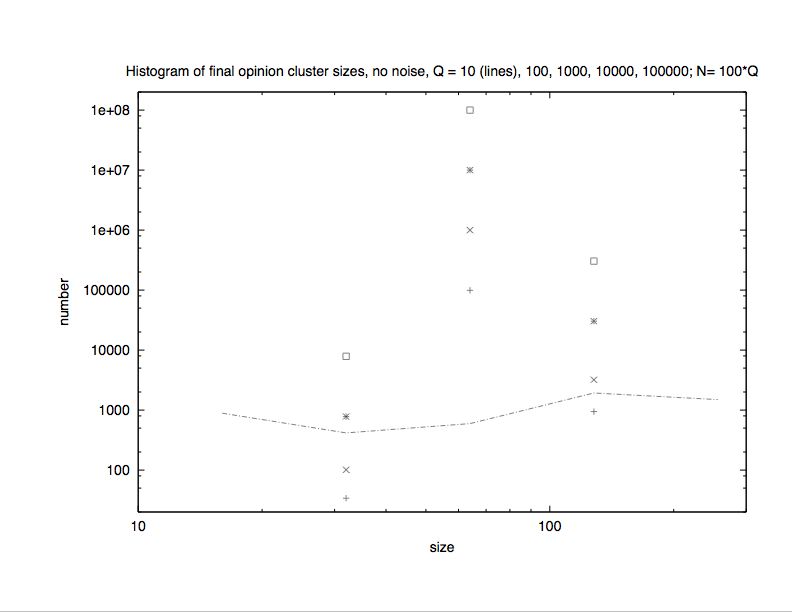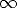In this sense the new results are in between the intensive S of (Deffuant 2000; Deffuant 2002; Weisbuch 2002; Ben-Naim 2003) and the extensive S of (Stauffer 2004). (Also in contrast to (Stauffer 2004), the histograms for the number of people sharing the same opinion show a single peak. As in (Stauffer 2004) people may share the same opinion even if they are disconnected.) Figure 3 shows that for a fixed ratio N/Q = 100 the cluster numbers are extensive.

Figure 3. Evidence that cluster numbers for fixed N/Q (here taken as 100) are extensive, for large systems up to 10 million nodes, with N and Q increasing from bottom to top. For small systems the results (line) are very different. All data are summed over 1000 runs.

2.4

Roughly the same results, Figure 4, are obtained if noise is introduced to simulate outside information in the opinion dynamics. Thus at each iteration, every agent after the above dynamics shifts the opinion by +1 with probability 1/4, by -1 with probability 1/4, and keeps it unchanged with probability 1/2. (However, the opinion cannot leave the interval from 1 to Q. The simulation stops if without this noise no opinion would have changed.) Thus the model is robust against this noise. Of course, now no complete consensus is found, not even at Q = 2. (If we follow (Deffuant 2000; Deffuant 2002; Weisbuch 2002) and allow everybody to interact with everybody, the results with noise are nearly the same as in Figure 4.)

Figure 4. As Fig.1, but with noise, for N = 10 (curve) to 10000. The straight line gives S = Q. For smaller Q at N > 100, no convergence within 106 iterations was found.

2.5

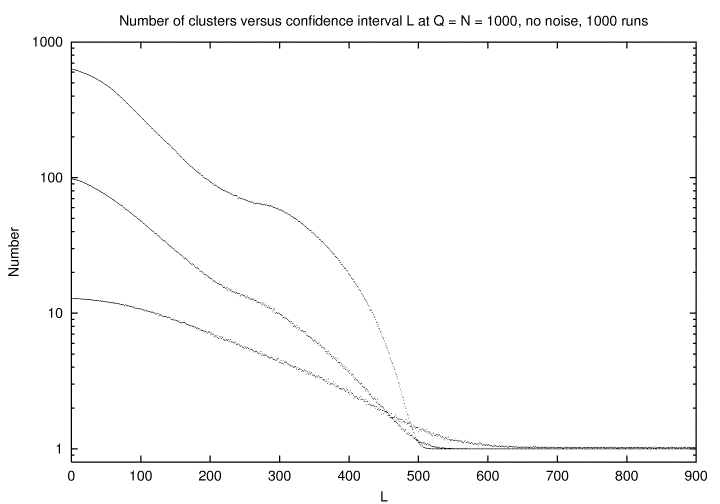
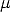The present model gets closer to the original Deffuant model if we introduce another free parameter L such that two people convince each other if their opinions do not differ by more than L units; L = 1 then is our previous discrete model. If Q and L both go to infinity at constant ratio d = L/Q, then this ratio is the d of Deffuant et al. The parameter of (Deffuant 2000; Deffuant 2002; Weisbuch 2002) was taken as 0.1^1/2. Figure 5 shows the variation of the number of surviving opinions with L, at fixed Q = 1000 and various N. No noise is used here since noise prevents convergence except for very small L. For Q = N = 5L the number of opinion clusters seems to vary proportional to N for large N.

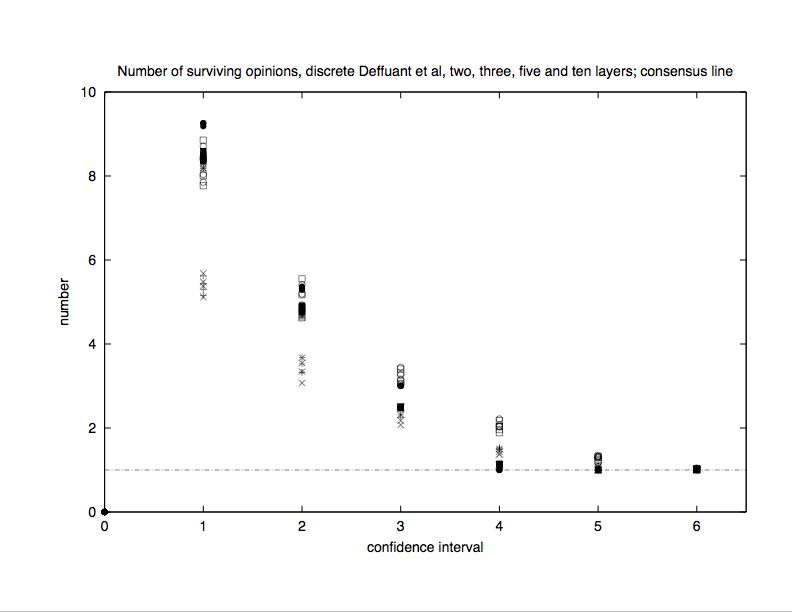
Figure 5. As Fig.1, no noise, for Q = 1000 as a function of the length L = Qd of the confidence interval, for N = 10, 100, 1000 (from bottom to top). The larger N is the more pronounced is the transition to complete consensus at L = 500 or d = 1/2.

Triads

3.1

Although the Barabási-Albert (Albert 2002; Barabási 2002; Stauffer 2004) network has successfully explained the scale-free nature of many networks, a striking discrepancy between it and real networks is that the value of the clustering coefficient - which is the probability that two nearest neighbours of the same node are also mutual neighbours - predicted by the theoretical model decays very fast with the network size and for large systems is typically several orders of magnitude lower than found empirically (it vanishes in the thermodynamic limit, Figure 6a). 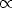In social networks (Davidsen 2002; Holme 2002; Szabó 2003), for instance, the clustering coefficient distribution C(k) exhibits a power-law behaviour, C(k) k^-, where k is number of neighbours (degree or connectivity) of the node and 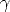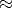1 (everyone in the network knows each other).

(a)
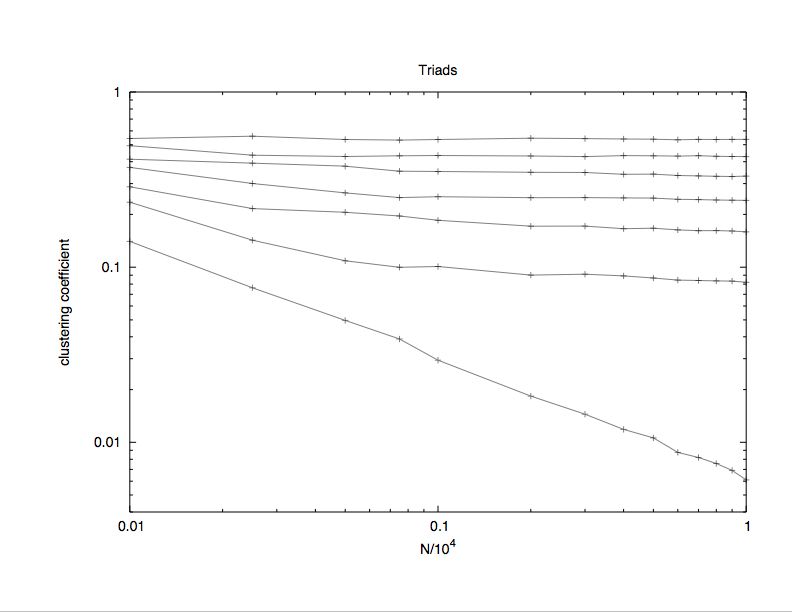
(b)
(c)
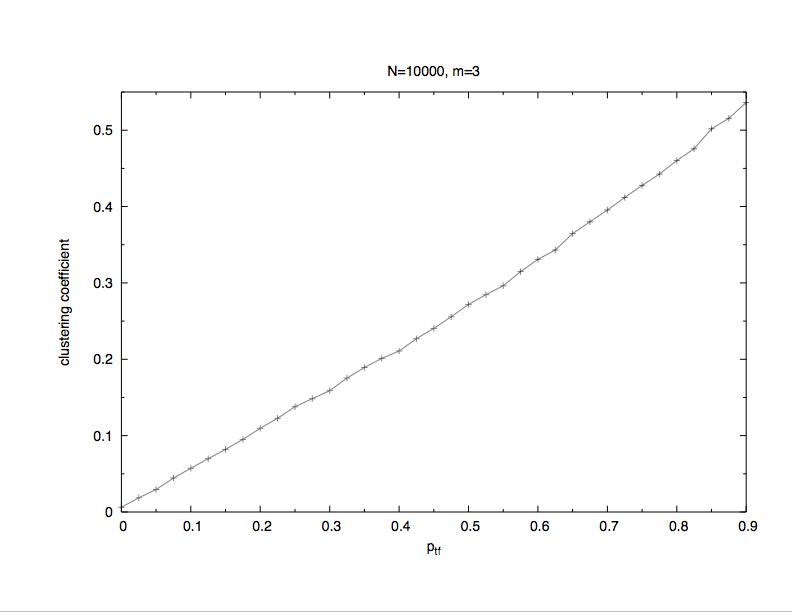
Figure 6. Triad formation: a) Log-log plot: Clustering coefficient versus the network size N at probability ptf = 0.00, 0.15, 0.30, 0.45, 0.60, 0.75. 0.90 (from bottom to top) to perform a triad formation step. b) Linear plot: Clustering coefficient versus the probability ptf to perform a triad formation step at N = 104. c) Log-log plot: Number of different surviving opinions versus total number Q of opinions, for various network sizes N on a scale-free network with triad formation step. The triad formation probability is ptf = 0.3

3.2

Very recently, by adding a triad formation step on the Barabási-Albert prescription, this problem has been surmounted and scale-free models with high clustering coefficient have been investigated (Davidsen 2002; Holme 2002; Szabó 2003). The algorithm is defined as follows: First, each new node performs a preferential attachment step, i.e, it is attached randoml to one of the existing nodes with a probability proportional to its degree; then follows a triad formation step with a probability p_tf: the new node selects at random a node in the neighbourhood of the one linked to in the previous preferential attachment step. If all neighbours are already connected to it, then a preferential attachment step is performed (“friends of friends get friends”). In this model, the original Barabási-Albert network corresponds to the case of p_tf = 0. It is expected that a nonzero P_tf gives a finite nonzero clustering coefficient as N is increased, and with the clustering coefficient going to zero when P_tf = 0 (the BA scale-free network model).

3.3

Simulations of the discretized version of the Deffuant model on this network produces similar results (see Figure 6) to those obtained using a Barabási-Albert network (Figure 1). The same behaviour was found for any value of the probability p_tf to perform a triad formation step. Furthermore, the clustering coefficient (Fig. 6b) agrees with the one predicted in (Davidsen 2002; Holme 2002; Szabó 2003), with a nearly linear increase with probability p_tf. (Other values of m give qualitatively the same behaviour.)

3.4

For completeness we end with some results from the directed model of (Stauffer 2004) on the size distribution of opinion clusters, those for the undirected case are similar. Figure 7 shows one peak for small sizes, with cluster numbers increasing proportional to the system size, and another peak for large sizes of the order of the network size, with small size-independent cluster numbers.

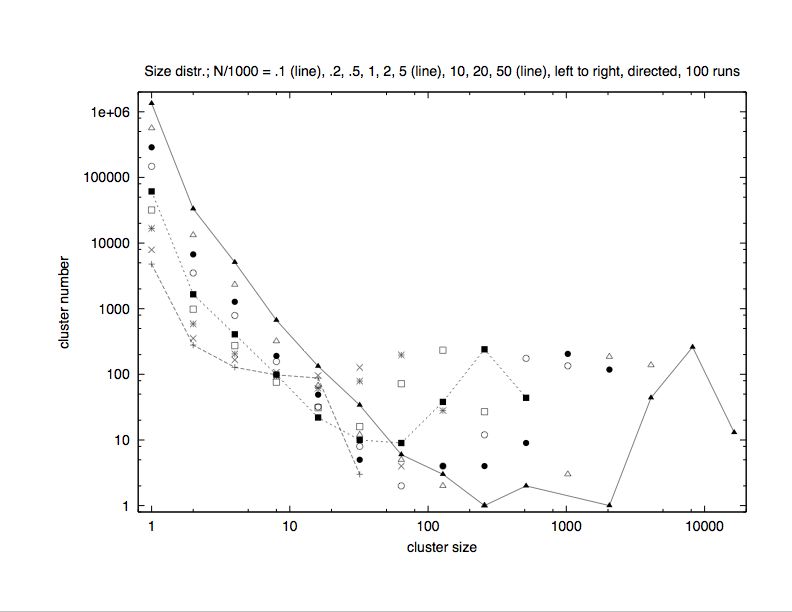
Figure 7. Size distribution for the clusters of different surviving opinions, summed over 100 samples, for network sizes N = 1000...50, 000 on the directed a scale-free network with continuous opinions as in the standard model (Deffuant 2000; Deffuant 2002; Weisbuch 2002).

Several layers

4.1

Following Schulze (Schulze 2004), we now put A copies of the same directed Barabási-Albert network on top of each other, with N agents on every layer. Each layer corresponds to a certain age cohort, with babies on the bottom (layer A), the oldest old on the top (layer 1), and intermediate ages in the A- 2 layers in between. Each person in every layer dies with probability p at each iteration. In case of death, the younger people on that position in the network move one layer up, keeping their opinion, and the lowest layer is occupied by a newly born baby getting the opinion of the parent. Initially, all people of different ages on the same position in the network share the same opinion, but later each layer draws its random numbers independently for random sequential updating. Thus it is crucial that the same network appears in A copies on top of each other, in order to have a unique identification of ancestors and offspring. We refrain from comparing the model with university teachers (full professors, associate professors, ..., down to teaching assistants) waiting for the superior to leave the job and make it available to younger ones.

4.2

Our simulations averaged over 1000 samples and four combinations of the number N of agents and the number Q of possible opinions: (N,Q) = (10,10), (100,10), (1000,10) and (10,1000). We used mortalities p = 0.01 and 0.5, maximum age A = 2, 3, 5, 10, and lengths L of the confidence interval = 1,2, ... 6 for Q = 10, and L = 10, 20,...60 for Q = 100. Figure 8 shows that only L/Q is really important: If it is 0.6 or higher, all samples lead to a full consensus with only one opinion surviving in all layers together. For small L the number S of surviving opinions is seen to be slightly below 10, the usual maximum number of opinions. Even for L = 1 and Q = 100 or 1000 (not shown) S remains of order ten if N = 10; we have to increase N to get larger S for larger Q. Also with N = 10000 and Q = 10 the results (not shown) look like in Figure 8a. Thus the basic result is similar to the monolayer results in Sec. 2: For small L/Q the number S of surviving opinions is of the order of N or Q, whatever is smaller. The number A of layers and the mortality p hardly influence the results.

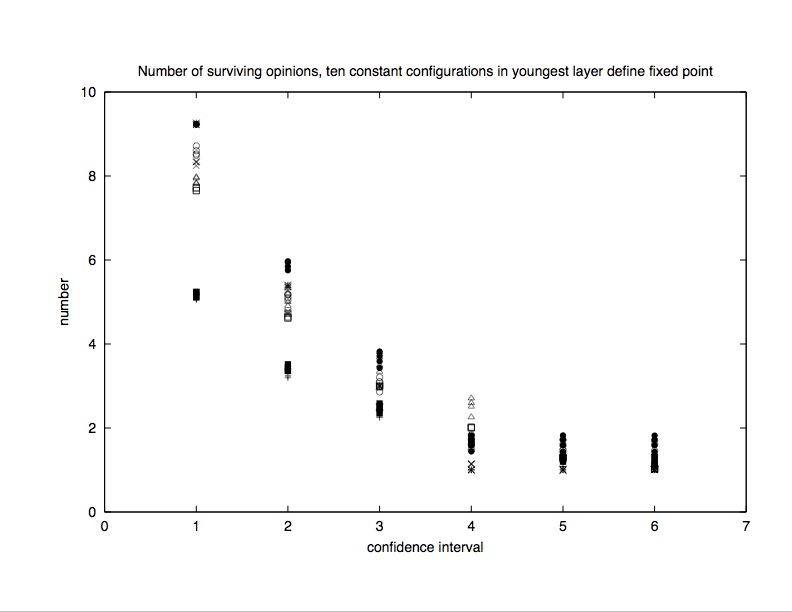
Figure 8. Multilayer model: Number of different surviving opinions versus confidence interval L for Q = 10 possible opinions. (For Q = 100 instead of 10 we plot the number versus L/10 instead of versus L, also in Figures 9 and 10.) We see complete consensus for L/Q > 0.6. Part (a) stops the simulation if in the whole system no one changed opinion during one iteration, while in part b we stopped it if the baby layer did not change over ten consecutive iterations.

4.3

In Figure 8a we let the simulations run, until during one iteration none of the A×N agents changed opinion. Figure 8b shows that the results are nearly the same if we follow (Schulze 2004) and stop the simulation when the baby layer remained unchanged during ten consecutive iterations; however, for L/Q > 0.6 instead only one surviving opinion we find on average between one and two.

4.4

Finally, we introduce advertising (Schulze 2003; Sznajd-Weron 2003) in favour of opinion q = 1: with 3 percent probability, every agent at every iteration had its opinion reduced by one unit. Now S is reduced and depends stronger on the various parameters, Figure 9. Again, for a confidence interval L/Q > 0.6 a complete consensus is found. Figure 10 shows for the same runs the success fraction: With what probability is the final opinion within one layer a consensus in the advertised opinion? For L/Q > 0.5 nearly complete success is seen.

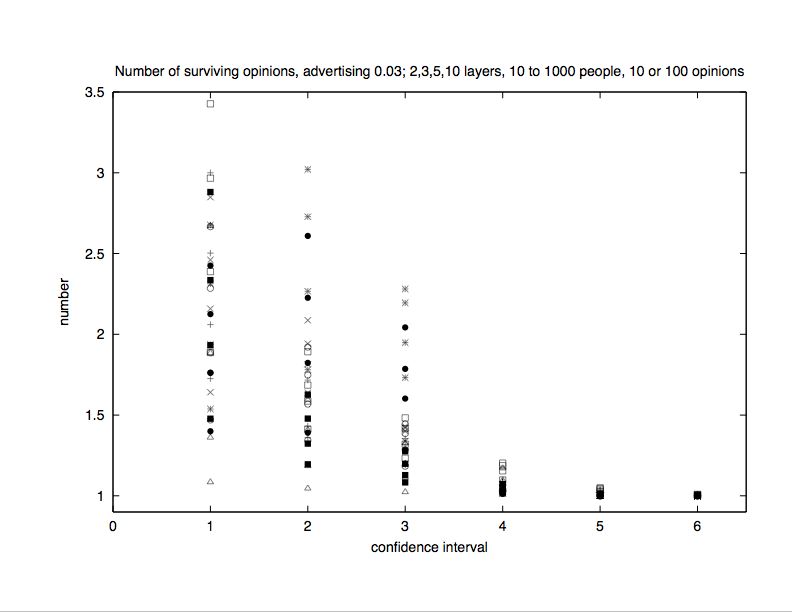
Figure 9. Number of different surviving opinions versus L in multilayer model in case of advertising. For a monolayer this number increases up to nearly 8.

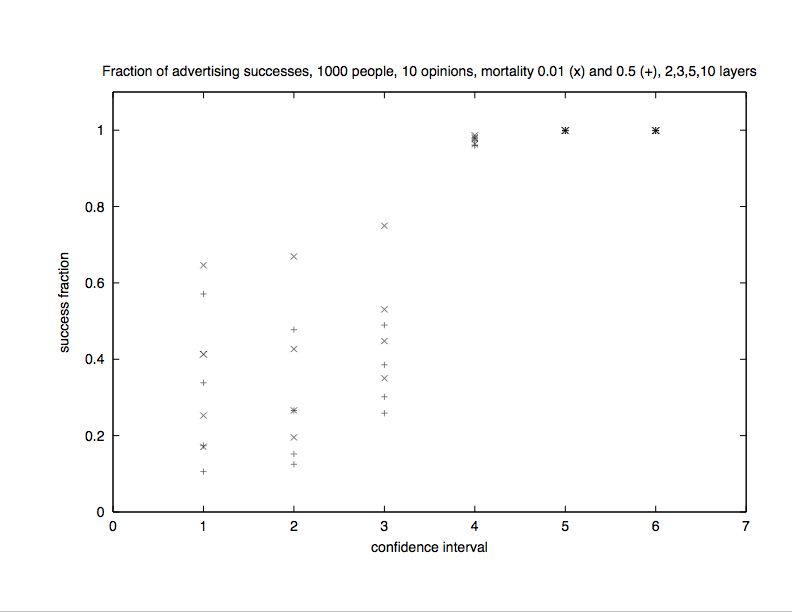
Figure 10. Fraction of advertising successes in multilayer model. For a monolayer the results for L/Q > 0.4 are similar but for L/Q = 0.1 the success fraction is at most 0.1. And for Q = 100 the monolayer success ratio was even lower.

Conclusions

5.1

By discretizing the opinions, the simulations of the Deffuant model could be simplified and made less ambiguous. Two limits are quite trivial: With many people and few opinions, nearly all opinions have some followers, and the number of final opinion clusters nearly agrees with the total number of opinions. In the opposite limit of many opinions for few people, nearly every person forms a separate opinion cluster. For the transition between these two limits, a simple scaling law is observed for the discretized opinions. At a fixed ratio of the number of people to the number of opinions, the number of final opinion clusters is extensive. Noise and a more realistic network with stronger clustering (Davidsen 2002; Holme 2002; Szabó 2003) do not change the results much in the discretized model. An ageing model with several layers representing different age groups gave results not much different from those of one single layer, also if advertising is included.

Acknowledgements

J. Holyst suggested to include noise, and J. Kertész to use the network of (Davidsen 2002; Holme 2002; Szabó 2003). A.O. Sousa thanks the Alexander von Humboldt Foundation for a grant.

Note

For more simulations of the Deffuant model see S. Fortunato, Int. J. Mod. Phys. C 15, No. 9; P. Assmann, preprint; and L. Sabatelli and P. Richmond, preprint.

Appendix

A.1

To facilitate others to continue this research, to state details unambiguously and to allow checks for possible errors, the main program used for section 2 is reproduced here. An electronic version is available from stauffer@thp.uni-koeln.de as deffuant14.f.

A.2

Loop 35 goes over various values of the confidence interval idis, loop 17 over nrun different samples. ibm is a random odd integer with 64 bits. All computations with derri... involve the Derrida-Flyvbjerg (Derrida 1986) parameter omitted from the text for simplicity and may be ignored by the reader. (The results for this parameter were similar to Weisbuch 2004.)

A.3

After initialization, loop 7 connects the initial core of the BA network, and loop 2 adds to it max sites i each of which builds m directed bonds to neighbours neighb(i,new), new=1,2,...m, selected randomly according to the BA rule with the help of the Kertész list of length L. After this network is built up, loop 5 initializes the opinions is randomly, and loop 9 makes the maxt iterations of the Deffuant process. In this process for each site j in loop 10 randomly a neighb(j,i) is selected, and if these two agree already or are too far from each other in their opinion, noting is done: goto 12. Otherwise the counter ichange is increased by one, thus giving the number of opinion pairs which have changed during this iteration. If both opinions differ only by one unit, one of them is selected randomly. If the opinion difference is greater than one (but not exceeding the confidence interval idis) then both opinions change by the same amount idiff according to the usual Deffuant rule. The lines adding noise to the opinion dynamics are commented out in this version. If loop 10 ends going through all sites j without having changed any opinion, the iterations stop: goto 11.

A.4

Now the analysis starts: nhist(i) counts how often opinion i is found in the final set of opinions is: loops 28 and 29. Loop 27 gives icount as the number of different surviving opinions, later averaged over many samples using ict to give the average number of different surviving opinions, i.e. the crucial quantity of this study. number is used for the binned size distribution ns of opinion clusters, and loops 33, 34, 31 can be ignored as mentioned above.

parameter(nsites=10  ,m=3,iseed=4711,maxt=1000000,iq=1000        1  ,nrun=1000,max=nsites+m, length=1+2*m*nsites+m*m)         integer*8 ibm,mult         dimension list(length),neighb(max,m),is(max),nhist(0:iq),        1 number(max), ns(31),irand(0:3)         data irand/0,0,-1,1/         w=sqrt(0.1)         print 100, iq, nsites, m, iseed, maxt, nrun, w    100  format('# directed, more confidence', 6i9,f6.3)         factor=(0.25d0/2147483648.0d0)/2147483648.0d0         facto2=factor*2*iq         mult=13**7         mult=mult*13**6         ibm=2*iseed-1         do 35 idis=100,900,100         derrisum=0.0         do 16 i=1,31    16     ns(i)=0         ict=0         do 17 irun=1,nrun           do 29 n=1,max    29       number(n)=0           do 7 i=1,m             do 7 nn=1,m               neighb(i,nn)=nn    7          list((i-1)*m+nn)=nn           L=m*m   c       All m initial sites are connected with each other and themselves           do 1 i=m+1,max             do 2 new=1,m    4          ibm=ibm*16807               j=1+(ibm*factor+0.5)*L               if(j.le.0.or.j.gt.L) goto 4               j=list(j)               list(L+new)=j               list(L+m+new)=i    2          neighb(i,new)=j    1        L=L+2*m   c     end of network and neighbourhood construction, start of opinion change           n=max         do 5 i=1,n           ibm=ibm*16807    5      is(i)=1+iabs(ibm)*facto2   c     print *, is         do 9 iter=1,maxt          ichange=0          do 10 j=1,n    6      ibm=ibm*16807           i=1+(ibm*factor+0.5)*m           if(i.le.0.or.i.gt.m) goto 6           i=neighb(j,i)           if(is(i).eq.is(j) .or. iabs(is(i)-is(j)).gt.idis) goto 12           ichange=ichange+1           if(iabs(is(i)-is(j)).eq.1) then             ibm=ibm*16807             if(ibm.lt.0) then               is(i)=is(j)             else               is(j)=is(i)             end if           else             idiff=isign(ifix(0.5+w*iabs((is(i)-is(j)))),is(i)-is(j))             is(j)=is(j)+idiff             is(i)=is(i)-idiff           endif   c10     print *, iter, is(j)    12     continue   c       ibm=ibm*mult   c       index=ishft(ibm,-62)   c       noise   c       is(j)=min0(iq,max0(irand(index)+is(j),1))    10     continue   c      if(iter.eq.(iter/1000 )*1000 ) print *, iter,ichange          if(ichange.eq.0)  goto 11    9    continue         print *, 'not converged'    11   continue         do 28 i=0,iq    28     nhist(i)=0         do 25 i=1,n           j=is(i)    25     nhist(j)=nhist(j)+1   c     print *, iter, nhist         icount=0         do 27 i=1,iq           if(nhist(i).gt.0) icount=icount+1           if(icount.gt.0) number(icount)=number(icount)+nhist(i)    27   continue         ict=ict+icount   c     print *, irun,icount,iter         icount=0         do 33 i=1,max    33     icount=icount+number(i)         derrida=0.0         fact=1.0/icount**2         do 34 i=1,max    34     derrida=derrida+fact*number(i)**2         do 31 i=1,max          if(number(i).eq.0) goto 31          ibin=1+alog(float(number(i)))/0.69315          ns(ibin)=ns(ibin)+1    31   continue   c     print *, irun,icount,iter,iq,derrida         derrisum=derrisum+derrida    17   continue         derrida=derrisum/nrun   c     do 32 i=1,31   c32   if(ns(i).gt.0) print *, 2**(i-1), ns(i)         call flush(6)    35   print *, idis, ict*1.0/nrun, derrida         stop         end

References

ALBERT, R. and Barabási, A.L. (2002), “Statistical mechanics of Complex networks”, Rev. Mod. Phys. 74, pp. 47-97.

AXELROD, R. (1997), “The Dissemination of Culture: A Model with Local Convergence and Global Polarization”, J. Conflict Resolut. 41, pp. 203-226; The Complexity of Cooperation: Agent-Based Models of Competition and Collaboration, Princeton University Press, Princeton NJ.

BARABÁSI, A.L. (2002), Linked: The New Science of Networks, Perseus Books Group, Cambridge MA.

BEN-NAIM, E., Krapivsky, P. and Redner, S. (2003), “Bifurcations and Patterns in Compromise Processes”, Physica D 183, pp. 190-204.

DAVIDSEN, J., Ebel, H. and Bornholdt, S. (2002), “Emergence of a small world from local interactions: Modeling acquaintance networks”, Phys.Rev.Letters 88, pp. 128701-1-128701-4.

DEFFUANT, G., Amblard, F., Weisbuch G. and Faure, T. (2002), “How can extremism prevail? A study based on the relative agreement interaction model”, Journal of Artificial Societies and Social Simulation 5 (4), paper 1 (https://www.jasss.org/5/4/1.html).

DEFFUANT, G., Neau, D. Amblard, F. and Weisbuch, G. (2000), “Mixing beliefs among interacting agents. Advances in Complex Systems”, Adv. Complex Syst. 3, pp. 87-98.

DERRIDA, B. and Flyvbjerg, H. (1986), “Multivalley structure in Kauffman’s model: analogy with spin glasses”, J. Phys. A 19, pp. L1003-L1008.

GALAM, S. (1990), “Social paradoxes of majority rule voting and renormalisation group”, J. Stat. Phys. 61, pp. 943-951 (1990).

GALAM, S. (1997), “Rational Group Decision Making: a random field Ising model at T=0”, Physica A 238, pp. 66-80.

HEGSELMANN, R. and Krause, U. (2002), “Opinion Dynamics and Bounded Confidence Models, Analysis and Simulation”, Journal of Artificial Societies and Social Simulation 5 (3), paper 2 (https://www.jasss.org/5/3/2.html).

HEGSELMANN, R. and Krause, U. (2004), “ Opinion Dynamics Driven by Various Ways of Averaging”, Physica A (in press) = http://pe.uni-bayreuth.de/?coid=18.

HOLME, P. and Kim, B.J. (2002), “Growing scale-free networks with tunable clustering”, Phys. Rev. E 65, pp. 026107-1-026107-4.

KRAUSE, U. (1997), “Soziale Dynamiken mit vielen Interakteuren. Eine Problemskizze”. In Krause, U. and Stöckler, M. (Eds.), Modellierung und Simulation von Dynamiken mit vielen interagierenden Akteuren, pp. 37-51, Bremen University, Bremen.

MOSS DE OLIVEIRA, S., de Oliveira, P.M.C. and Stauffer, D. (1999): Evolution, Money, War and Computers, Teubner, Stuttgart and Leipzig.

SCHULZE, C. (2003), “Advertising in the Sznajd Marketing Model”, Int. J. Mod. Phys. C 14, pp. 95-98.

SCHULZE, C. (2004), “Advertising, consensus, and ageing in multilayer Sznajd model”, Int. J. Mod. Phys. C 15, No. 4 (in press) = cond-mat/0312342.

SCHWEITZER, F. (2003), Brownian Agents and Active Particles, Springer, Berlin.

STAUFFER, D. (2002), “Monte Carlo simulations of Sznajd models”, Journal of Artificial Societies and Social Simulation 5 (1), paper 4 (https://www.jasss.org/5/1/contents.html).

STAUFFER, D. (2003), “Sociophysics Simulations”, Computing in Science and Engineering 5 (3), pp. 71-75; “How to Convince Others? Monte Carlo Simulations of the Sznajd Model” , in AIP Conference Proceedings, The Monte Carlo Method on the Physical Sciences: Celebrating the 50th Anniversary of the Metropolis Algorithm, edited by Gubernatis, J.E., 690, pp. 147-155 = cond-mat/0307133.

STAUFFER, D., Sousa, A.O and Moss de Oliveira, S. (2000), “Generalization to Square Lattice of Sznajd Sociophysics Model”, Int. J. Mod. Phys. C 11, pp. 1239-1245.

STAUFFER, D. and Meyer-Ortmanns, H. (2004), “Simulation of Consensus Model of Deffuant et al on a Barabasi-Albert Network”, Int. J. Mod. Phys. C 15 (2) 241 - 246.

SZABÓ, G., Alava, M. and Kertész, J. (2003), “Structural transitions in scale-free networks”, Phys. Rev. E 67, pp. 056102-1-056102-1.

SZNAJD-WERON, K. and Sznajd, J. (2000), “Opinion Evolution in Closed Community”, Int. J. Mod. Phys. C 11, 1157 - 1166.

SZNAJD-WERON, K. and Weron, R.(2003), “How effective is advertising in duopoly markets?”, Physica A 324, pp. 437-444.

WEIDLICH, W. (2000), Sociodynamics; A Systematic Approach to Mathematical Modelling in the Social Sciences, Harwood Academic Publishers, Amsterdam.

WEISBUCH, G., Deffuant, G., Amblard, F. and Nadal, J.-P. (2002), “Meet, Discuss, and Segregate!”, Complexity 7, pp. 55-63.

WEISBUCH, G. (2004), “Bounded confidence and social networks”, Eur. Phys. J. B, Special Issue: Application of Complex Networks in Biological Information and Physical Systems volume 38, pp.339-343.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2004]