Gary Mckeown and Noel Sheehy (2006)
Mass Media and Polarisation Processes in the Bounded Confidence Model of Opinion Dynamics
Journal of Artificial Societies and Social Simulation
vol. 9, no. 1
<https://www.jasss.org/9/1/11.html>
For information about citing this article, click here
Received: 17-Jun-2005 Accepted: 27-Oct-2005 Published: 31-Jan-2006
 Abstract
Abstract
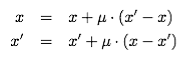
|
(1) |
where μ is the convergence parameter (Deffuant et al., 2000). Like the original model all initial opinions are randomly generated across a uniform distribution between 0 and 1 (or later -1 and 1).
|
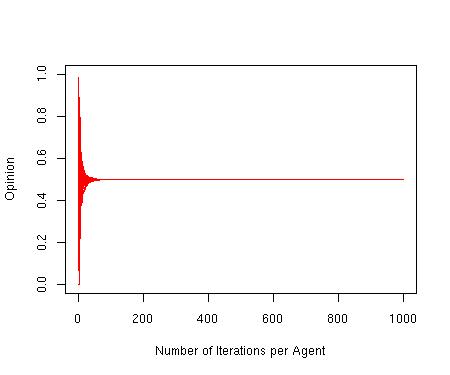
| Figure 1. Convergence to a Central Opinion. p = 0, d = 0.5, μ = 0.3, n = 100, N = 2500 |
|
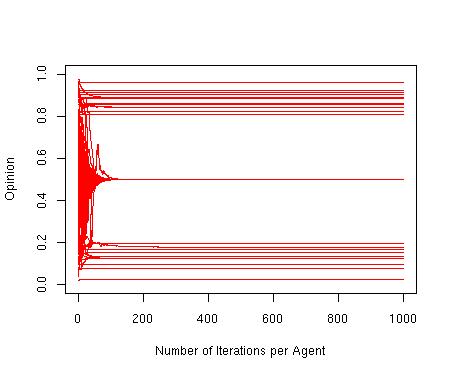
| Figure 2. Central Convergence with Isolated Extremes. p = 0, d = 0.25, μ = 0.3, n = 100, N = 2500 |
|
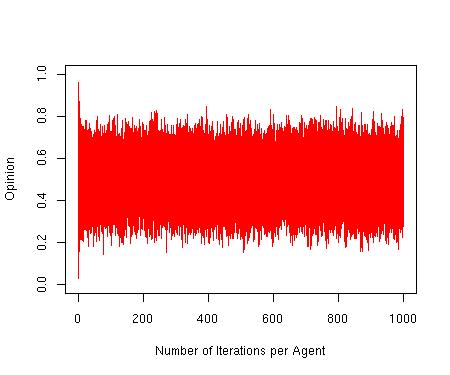
| Figure 3. Opinion in a state of constant change around a Central Opinion. p = 1, d = 0.7, μ = 0.3, n = 100, N = 2500 |
|
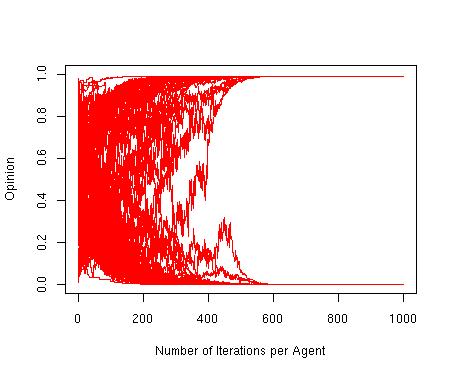
| Figure 4. Opinion settles in two extreme groups. p = 1, d = 0.4, μ = 0.3, n = 100, N = 2500 |
|
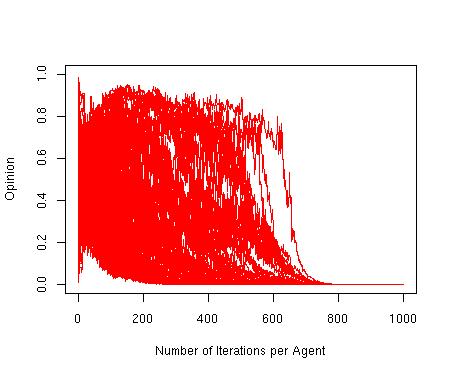
| Figure 5. Opinion settles at one extreme after a period of persistent opinion exchange. p = 1, d = 0.5, μ = 0.3, n = 100, N = 2500 |
|
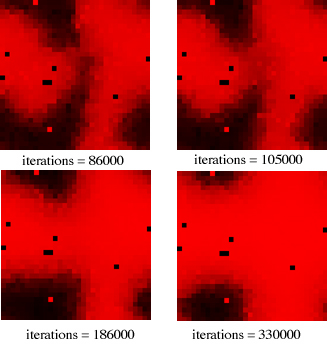
| Figure 6. A sequence of screenshots showing two groups of opinion and with gradients of opinion exchange. p = 1, d = 0.5, μ = 0.3, n = 100, N = 2500, Red = 1, Black = 0, one iteration = a single opinion exchange |
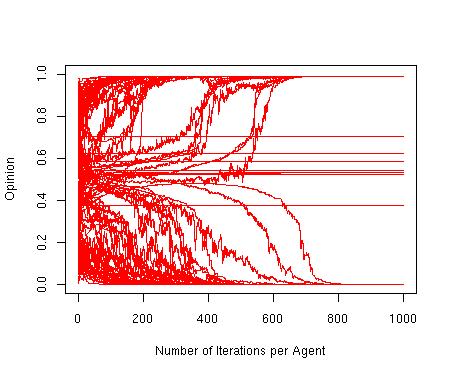
|
| Figure 7. Convergence at extremes with Isolated Moderate Opinions. p = 1, d = 0.25, μ = 0.3, n = 100, N = 2500 |
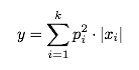
|
(2) |
|
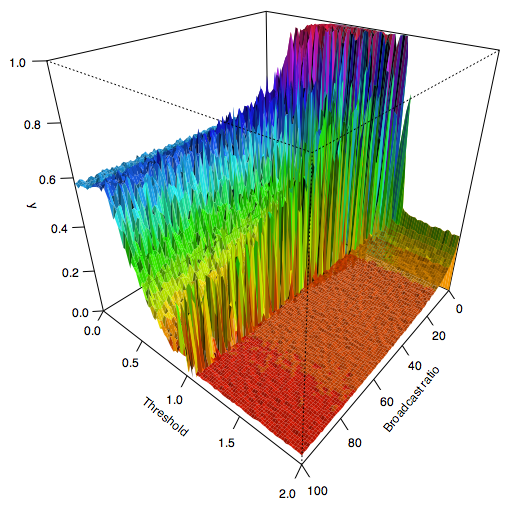
| Figure 8a. Standard Deviations for Threshold and Broadcast Ratio after an average of 1000 iterations per agent |
|
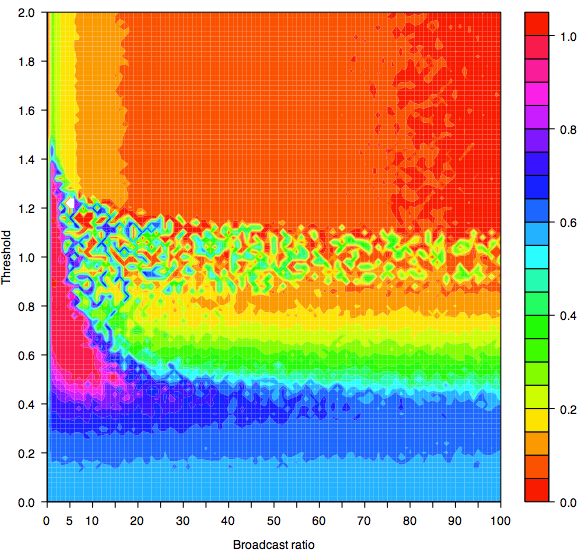
| Figure 8b. Contour graph showing Standard Deviations for Threshold and Broadcast Ratio after an average of 1000 iterations per agent |
|
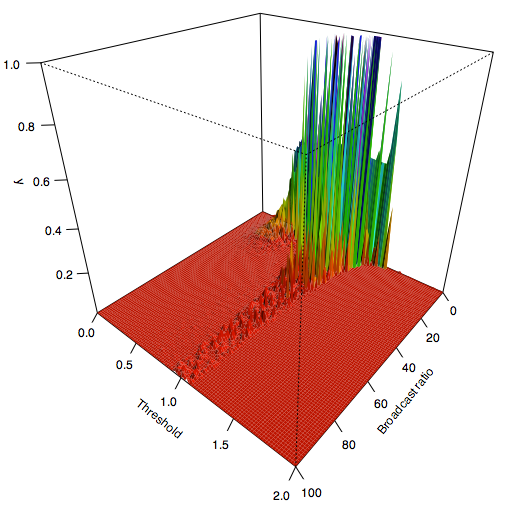
| Figure 9a. The indicator y for Threshold and Broadcast Ratio after an average of 1000 iterations per agent |
|
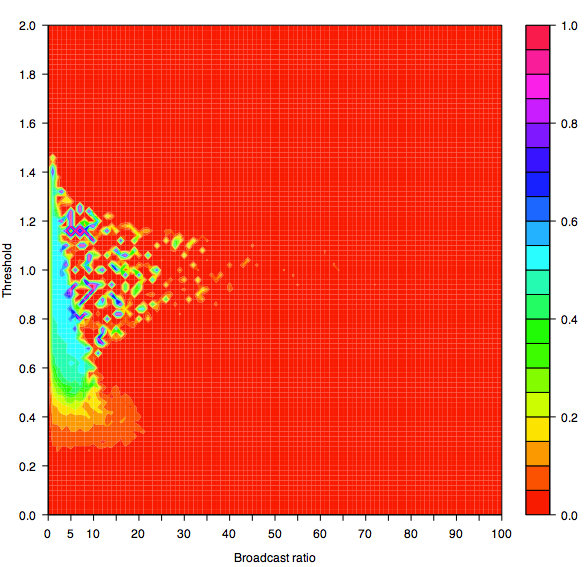
| Figure 9b. Contour graph showing the indicator y for Threshold and Broadcast Ratio after an average of 1000 iterations per agent |
|
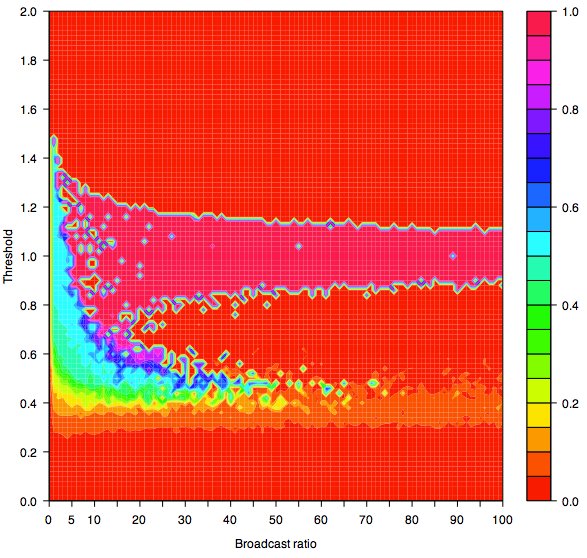
| Figure 9c. Contour graph showing the indicator y for Threshold and Broadcast Ratio after an average of 10000 iterations per agent |
|
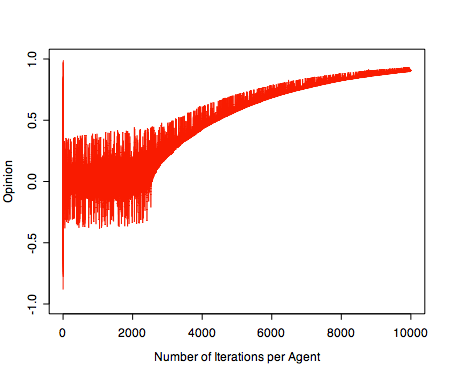
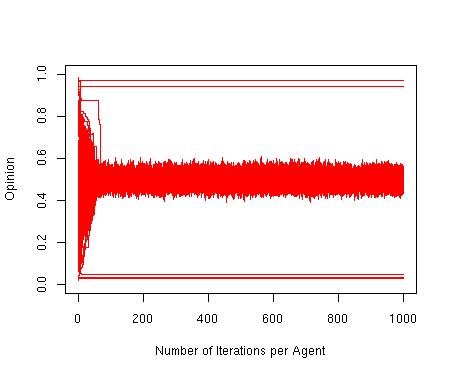
| Figure 10. Single extreme convergence with a broadcast ratio of 1:100 for 10000 iterations. p = 1, d = 1, μ = 0.3, n = 100, N = 2500 |
|
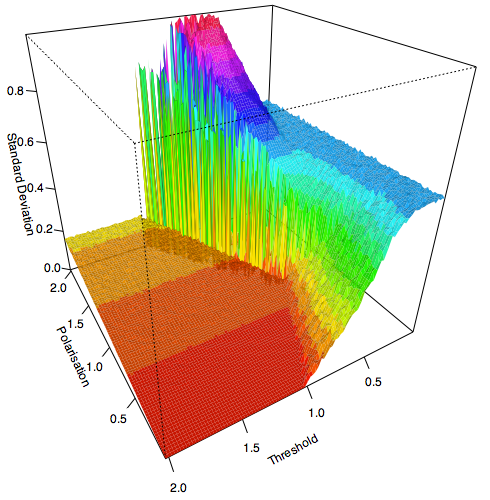
| Figure 11a. Standard Deviations for Threshold and Polarisation after an average of 10000 iterations per agent |
|
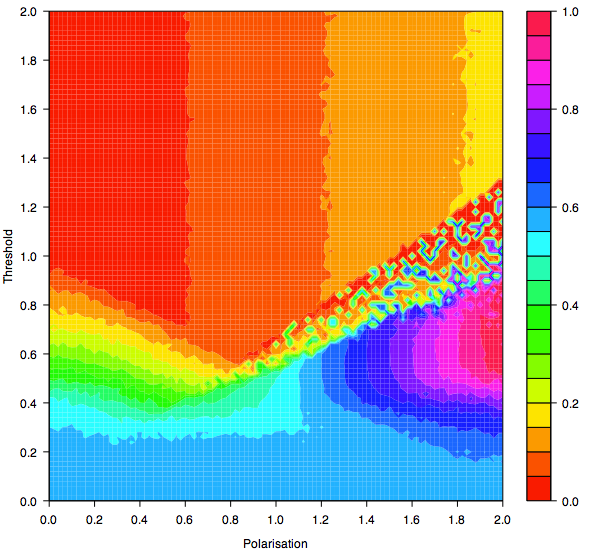
| Figure 11b. Contour graph showing Standard Deviations for Threshold and Polarisation after an average of 10000 iterations per agent |
|
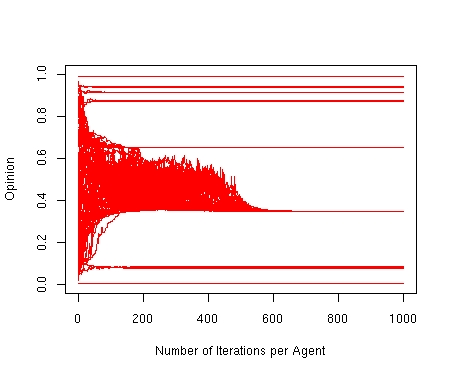
| Figure 12. Constant change of central opinions with islands of extremists with homogenous opinions. p = 0.3, d = 0.25, μ = 0.3, n = 100, N = 2500 |
|
| Figure 13. Constant change of central opinions with islands of extremists with homogenous opinions. p = 0.3, d = 0.25, μ = 0.3, n = 100, N = 2500 |
|
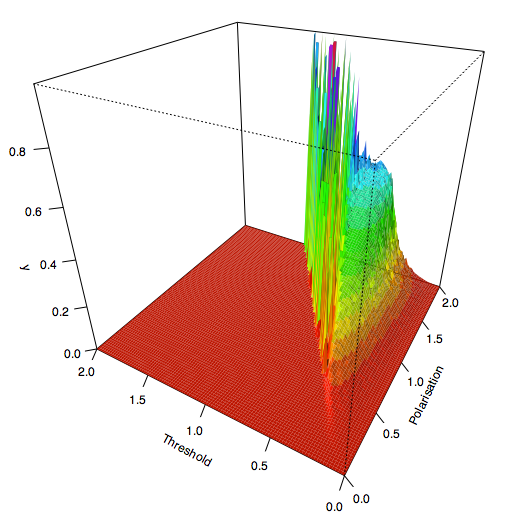
| Figure 14a. The indicator y for Threshold and Polarisation after an average of 1000 iterations per agent |
|
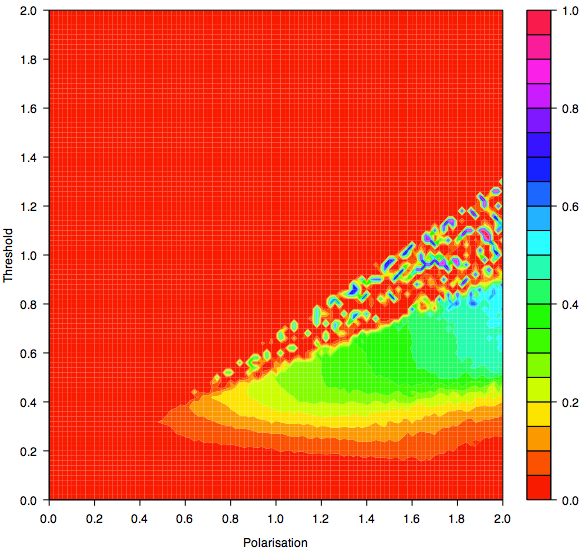
| Figure 14b. Contour graph showing the indicator y for Threshold and Polarisation after an average of 1000 iterations per agent |
|
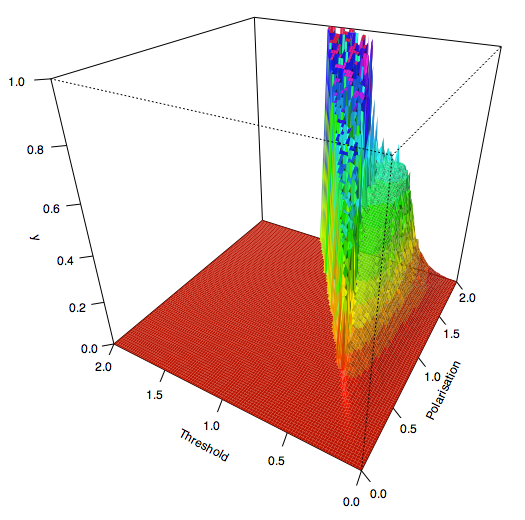
| Figure 15a. The indicator y for Threshold and Polarisation after an average of 10000 iterations per agent |
|
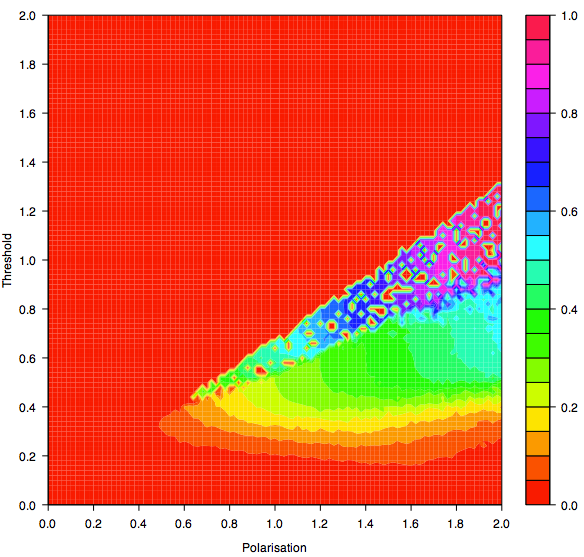
| Figure 15b. Contour graph showing the indicator y for Threshold and Polarisation after an average of 10000 iterations per agent |
|
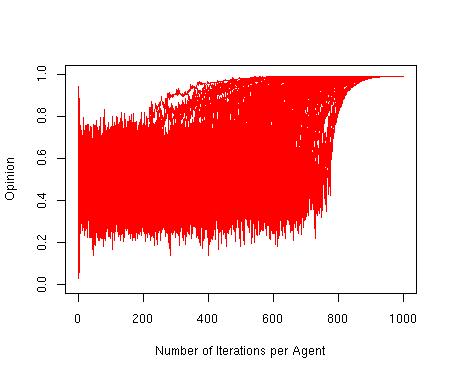
| Figure 16. Straying from one regime to another. p = 1, d = 0.64, μ = 0.3, n = 100, N = 2500 |
|
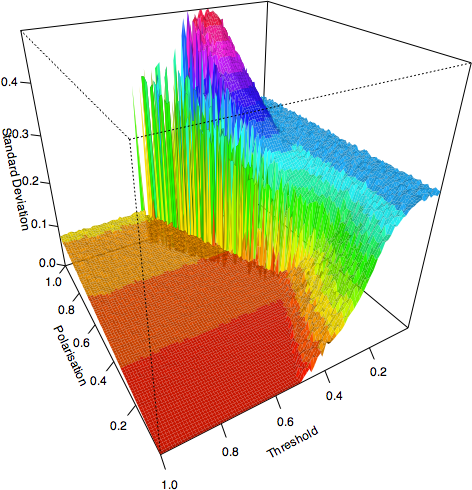
| Figure 17a. Standard Deviations for Threshold and Polarisation using a Moore nieghbourhood with 8 neighbours after an average of 1000 iterations per agent |
|
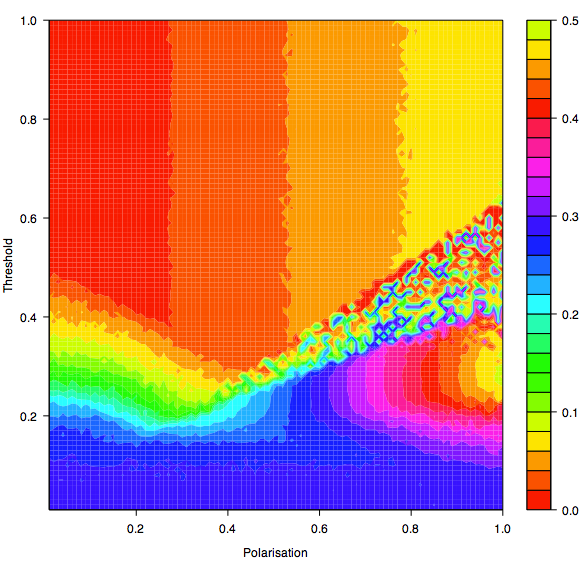
| Figure 17b. Standard Deviations for Threshold and Polarisation using a Moore neighbourhood with 8 neighbours after an average of 1000 iterations per agent |
AMBLARD, F., and Deffuant, G. (2004) The role of network topology on extremism propagation with the relative agreement opinion dynamics. Physica A: Statistical Mechanics and its Applications, 343: 725-738
DEFFUANT, G., Neau, D., Amblard, F., and Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 3(1-4):87-98.
DEFFUANT, G., Amblard, F., Weisbuch, G., and Faure, T. (2002). How can extremism prevail? a study based on the relative agreement interaction model. Journal of Artificial Societies and Social Simulation, 5 (4). https://www.jasss.org/5/4/1.html
DEFFUANT, G., Amblard, F., and Weisbuch, G. (2004) Modelling Group Opinion Shift to Extreme: the Smooth Bounded Confidence Model. European Social Simulation Association, 2nd Annual Conference, Valladolid, Spain, 2004.
DITTMER, J.C. (2001). Consensus formation under bounded confidence. Nonlinear Analysis, (47):4615 - 4621.
GALAM, S. (1997). Rational group decision making: A random field Ising model at T = 0. Physica A: Statistical Mechanics and its Applications, 238: 66-80.
GALAM, S. and Wonczak, S. (2000). Dictatorship from majority rule voting. The European Physical Journal B, 18:183-186.
HEGSELMANN, R. and Krause, U. (2002). Opinion dynamics and bounded confidence: models, analysis and simulation. Journal of Artificial Societies and Social Simulation, 5 (3). https://www.jasss.org/5/3/2.html
HOLYST, J. A., Kacperski, K., and Schweitzer, F. (2000). Phase transitions in social impact models of opinion formation. Physica A: Statistical Mechanics and its Applications, 285 (Issues 1-2):199-210.
KACPERSKI, K., and Holyst, J. A. (2000). Phase transitions as a persistent feature of groups with leaders in models of opinion formation. Physica A: Statistical Mechanics and its Applications, 287: 631-643.
SCHULZE, C. (2003). Advertising in the sznajd marketing model. International Journal of Modern Physics C: Physics & Computers, 14(1):95.
STAUFFER, D. (2005). Sociophysics simulations ii: Opinion dynamics. http://arxiv.org/pdf/physics/0503115
STAUFFER, D., Sousa, A., and Schulze, C. (2004). Discretized opinion dynamics of the deffuant model on scale-free networks. Journal of Artificial Societies and Social Simulation, 7(3). https://www.jasss.org/7/3/7.html
SZNAJD-WERON, K. and Sznajd, J. (2000). Opinion evolution in closed community. International Journal of Modern Physics C: Physics & Computers, 11(6):1157.
SZNAJD-WERON, K. and Weron, R. (2003). How effective is advertising in duopoly markets? Physica A: Statistical Mechanics and its Applications, 324(1-2):437-444.
WATTS, D.J., and Strogatz, S.H. (1998). Collective dynamics of small-world networks, Nature 393 440-442.
WEISBUCH, G., Deffuant, G., and Amblard, F. (2005) Persuasion dynamics. Physica A: Statistical Mechanics and its Applications, 353: 555-575
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2006]