Abstract
Abstract
- Resource reallocation problems are common in real life and therefore gain an increasing interest in Computer Science and Economics. Such problems consider agents living in a society and negotiating their resources with each other in order to improve the welfare of the population. In many studies however, the unrealistic context considered, where agents have a flawless knowledge and unlimited interaction abilities, impedes the application of these techniques in real life problematics. In this paper, we study how agents should behave in order to maximize the welfare of the society. We propose a multi-agent method based on autonomous agents endowed with a local knowledge and local interactions. Our approach features a more realistic environment based on social networks, inside which we provide the behavior for the agents and the negotiation settings required for them to lead the negotiation processes towards socially optimal allocations. We prove that bilateral transactions of restricted cardinality are sufficient in practice to converge towards an optimal solution for different social objectives. An experimental study supports our claims and highlights the impact of a realistic environment on the efficiency of the techniques utilized.
- Keywords:
- Resource Allocation, Negotiation, Social Welfare, Agent Society, Behavior, Emergence
 Introduction
Introduction
- 1.1
-
In the past few years, an increasing number of studies focused on
resource allocation problems, either from a centralized or a distributed point of view. Optimally allocating a set of resources
between agents in an artificial society is an important issue in
Computer Science as well as in Economics. Indeed, numerous
applications can be formulated as allocation problems in various
domains ranging from auctions (Bachrach & Rosenschein, 2008; Sandholm, 2002) to industrial procurement
(Giovannucci et al., 2004), including grid computing (Galstyan et al., 2005).
- 1.2
-
Centralized solving techniques only aim to determine the best way to
assign resources in order to optimize the objective function, without
consideration for their origin. At the opposite, distributed solving
techniques consider that resources are initially allocated between
agents, and the aim is to determine a sequence of transactions leading
to an optimal allocation. However, most of these techniques
cannot be used in practice: either they do not consider some
constraints inherent to the application context or they rely on
unrealistic assumptions. For instance, in many studies
(e.g. Endriss et al., (2006) or Chevaleyre et al., (2010), agents can
compensate disadvantageous transactions using money from an
infinite wallet. This way, any condition on a transaction can be
satisfied. Similarly, relationships between agents are often not
considered whereas this characteristic occurs in many
applications. Indeed, agents in the population usually all know each other and can negotiate freely with each other. However, communications
are often restricted in a significant number of applications
(Lieberman et al., 2005): business, spatial, applications based on social
networks or Internet applications. Most of the time, these studies
rely on omniscient agents which know everything about everybody
(i.e. flawless knowledge of the whole society). However, in large-scale
applications (with a large number of agents), the agents only have access to local
information. Since these assumptions are not plausible from our point
of view, we choose to consider a more realistic environment where
agents have incomplete knowledge and limited interaction
possibilities.
- 1.3
-
The aim of this paper is not to prove the existence of solutions with
respect to a specific context (it is certainly important but not
sufficient in practice) but to propose a distributed mechanism based
on agent negotiations and which can be used in a more realistic
context. Our objective is to design the agent behavior and the
negotiation settings to implement accordingly in order to lead the
negotiation processes towards the best solutions. These solutions,
which are achieved by an adaptive and anytime algorithm, can be considered as emergent.
- 1.4
-
This paper is structured as follows. Section 2
presents the limitations of the current studies on allocation
problems. Section 3 defines some basic notions and
describes what, from our point of view, is a more realistic environment. The different parameters on which relies the solving method we propose are also presented.
Section 4 introduces the
simulation protocol and discusses about the evaluation of agent
negotiations. Characteristics favoring the achievement of socially
interesting allocations are also analyzed with respect to the
utilitarian and the egalitarian welfare
notions. Section 7 concludes this study with a
summary of the most efficient negotiation settings according to
different scenarios.
 Background
Background
- 2.1
-
Different ways exist in the literature to evaluate the quality of resource allocations. One of them, called social efficiency, can be measured owing to notions from the social choice theory (Moulin, 1988; Arrow et al., 2002). These notions evaluate different aspects of allocations in a global way, aggregating the satisfaction of all the agents. The average satisfaction is evaluated according to the utilitarian welfare. The egalitarian welfare focuses on the weakest satisfaction. The Nash product considers both fairness and average satisfaction while elitist societies only consider the largest satisfaction. These four welfare notions are the most important and the most widely used to date (Endriss et al., 2006; Chevaleyre et al., 2010; Ramezani & Endriss, 2009; Brams & Taylor, 1996) and only those will be considered in this paper for this reason.
- 2.2
- The Pareto efficiency is also an omnipresent notion in the literature (Moulin, 1988; Arrow et al., 2002). An allocation is Pareto-efficient if there does not exist another allocation that would increase the satisfaction of an agent without decreasing the satisfaction of any other agent. This notion is useful when agents are purely self-centered. However, in this paper, the objective is to find the best agent behavior to maximize the welfare of the agent society. Thus, selfless agents are also considered. In such a case, the Pareto efficiency appears as a less interesting notion and is not considered in this paper.
- 2.3
- Many studies focusing on the different aspects of allocation problems evaluate the allocations using the welfare notions mentioned above. For instance, Sandholm, (Sandholm, 1998) establishes essential theoretical results for allocation problems in utilitarian societies. He classifies the different kinds of transaction and he also demonstrates the existence of transaction sequences leading to optimal solutions depending on the kinds of transaction allowed during negotiations. Other studies extend this theoretical work like (Endriss et al., 2006; Chevaleyre et al., 2010). They consider different welfare functions and design various scenarios according to many representations of agents preferences. They establish convergence results on negotiation processes according to these scenarios. Complexity of allocation problems is investigated as well. The computational complexity is analyzed to check the sufficiency of transactions involving one resource at a time in given cases (Dunne et al., 2005; Dunne & Chevaleyre, 2008). These papers characterize solutions, studying the desirable properties according to different scenarios. However, these studies do not focus on the mechanism required in practice to achieve a solution maximizing the welfare of a society. These studies are based on omniscient agents that can negotiate without restrictions. Only self-centered agents are considered and collaboration is meaningless.
- 2.4
-
In (Chevaleyre et al., 2007), authors study the allocation of goods
to eliminate envy within a population. They establish convergence and
complexity results on graph allocation problems. The authors do not
consider the agent behaviour to implement in order to achieve optimal
solutions in practice. Task allocation problems are also studied when
communication abilities between agents are restricted (de Weerdt et al., 2007). The authors only consider the utilitarian perspective of the
problem and propose some exponential algorithms. Simulations are
performed on random graphs of different kinds (small-world, scale-free,
...). Some authors focus on topological issues, where the behaviour and
the performance of complex systems are studied according to topological
characteristics (Dekker, 2007)). Instead of studying allocation problems
in a generic way, some authors focus on a specific game, e.g. the
ultimatum game, and study the evolution of fairness on complex networks
(Xianyu, 2010). Some studies focus on dynamic populations. For instance,
(Zoethout et al., 2010) studies the impact of a newcomer on the
efficiency and the performance according to different scenarios. The
authors use different performance indicators that can be compared to
social measures. The time performance of the slowest agent corresponds
to an egalitarian metric whereas the sum of the individual performances
of all the agents (the labour cost) corresponds to an utilitarian point
of view. In this paper, the environment is static: the size of the
artificial society and the total number of resources do not vary.
 Multiagent resource allocation problem
Multiagent resource allocation problem
- 3.1
-
In this section, resource allocation problems are defined and
characterized according to several crucial parameters. We describe
our claim for a more realistic environment and we
discuss about its importance and its impact on the efficiency of
solving techniques. Different elements on which our agent-based
solving method relies are finally described (Nongaillard et al., 2008). All the
concepts are defined in such a way that their distributed
implementation is facilitated.
Basic notions - 3.2
-
Allocation problems are usually defined based on a population of
agents and on a set of resources. The agents express their preferences on all
the resources and have a bundle containing their own resources. The aim of
resource allocation problems is to find an allocation, i.e. an
assignment of the set of resources between the agents of the
population, maximizing (or minimizing) a given objective.
- 3.3
-
Several parameters affect the properties of an allocation problem. Even
a slight difference between the characteristics of two allocation
problems can have a fundamental impact on the way these problems can be solved efficiently.
One of these crucial parameters is the nature of the
resources considered. It affects directly the properties of resource
allocations.
- 3.4
-
In this paper, resources are assumed atomic, not shareable and
unique. Since resources are assumed atomic, agents cannot
divide them in order to trade only a part. For instance, a book is an
atomic resource: trading it page by page is impossible. Resources are
not shareable which means the satisfaction of an agent only
depends on the resources in its bundle, i.e. resources that belong to
another agent cannot be considered in the evaluation of the
satisfaction of the agent. Finally, resources are unique and
tagged with a unique identification number. Such an environment is
called single-unit (in contrast with a multi-unit environment
where several similar resources cannot be distinguished). For
instance, let us consider a box of 8 eggs. It is possible either to
consider the whole box as an atomic resource or to consider each egg
as a resource. In the latter case, owning the first egg of the box is
not equivalent to owning the last one. Both cases correspond to two
different resource allocations.
- 3.5
-
According to these characteristics, a resource allocation can be
defined more formally as follows:
Definition 1 (Allocation) Given a set
 of m resources and a population
of m resources and a population
 of n agents, a resource allocation
A is an ordered list of n resource
bundles
Ri⊆
of n agents, a resource allocation
A is an ordered list of n resource
bundles
Ri⊆ describing the
resources owned by each agent i:
A = [R1,..., Rn], 1,..., n∈where
describing the
resources owned by each agent i:
A = [R1,..., Rn], 1,..., n∈where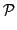 , A∈
, A∈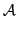 .
.
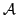 is the set of all possible allocations. A
resource allocation also satisfies the following properties:
In other words, an allocation is constituted by the ordered list of the agent bundles. Moreover all the resources must be allocated to the agents and a resource can only belong to one agent at a time.
is the set of all possible allocations. A
resource allocation also satisfies the following properties:
In other words, an allocation is constituted by the ordered list of the agent bundles. Moreover all the resources must be allocated to the agents and a resource can only belong to one agent at a time.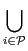 Ri =
Ri = 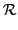 ,
, 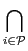 Ri = ∅, and A(i) = Ri, i∈
Ri = ∅, and A(i) = Ri, i∈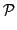 .
.
- 3.6
-
As described in Section 1, this paper focuses on
distributed methods based on agent negotiations according to a more
realistic context. We assume the knowledge of an agent is incomplete: an agent only knows its preferences, its bundle of resources and a list of neighbors (agents with which interactions are
possible). This way, each agent is able to negotiate with the restricted
number of agents formed by its neighborhood. The agents also negotiate
according to a given policy: the transactions they use for trading resources belong to a given set.
A negotiation problem can thus be defined more formally as follows:
Definition 2 (Negotiation problem) A negotiation problem is a tuple
〈 ,
,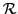 , Δ,
, Δ,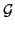 〉, where
〉, where
 = {1,..., n} is a finite population of
n agents,
= {1,..., n} is a finite population of
n agents,
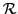 = {r1,..., rm} is a finite set of m
resources, Δ is a set containing the kinds of transaction allowed during
the negotiations, and
= {r1,..., rm} is a finite set of m
resources, Δ is a set containing the kinds of transaction allowed during
the negotiations, and
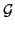 is the contact graph.
is the contact graph. - 3.7
-
Restrictions on the communications between agents are modeled by a contact
graph
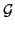 where the nodes represent the agents and the edges represent the
interaction possibilities between the agents so that two agents linked in the graph can negotiate together.
Note that in practice this graph is distributed among the agents of
population
where the nodes represent the agents and the edges represent the
interaction possibilities between the agents so that two agents linked in the graph can negotiate together.
Note that in practice this graph is distributed among the agents of
population
 as agent neighborhoods.
Definition 3 (Contact graph) A contact graph is an undirected graph
as agent neighborhoods.
Definition 3 (Contact graph) A contact graph is an undirected graph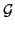 = (
= ( ,
,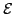 ). Two agents can communicate if an edge from
). Two agents can communicate if an edge from
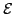 between
them exists. Note that this relation is symmetric.
between
them exists. Note that this relation is symmetric. - 3.8
-
An agent can be defined in a generic way by a resource bundle, a
valuation function describing its preferences, a list of agents (also
called neighbors) with which it is able to communicate, a behavior
describing how it negotiates with others and an acceptability criterion
related to its decision-making.
Definition 4 (Agent) An agent i∈
 is a tuple
〈Ri, vi, Bi, Ci, Ni〉, where
Ri is the set of mi resources
the agent owns, vi is the valuation function (the
agent preferences), Ni is the list of
ni neighbors, Bi
defines the agent behavior according to which the agent negotiates,
and Ci is its acceptability criterion on which
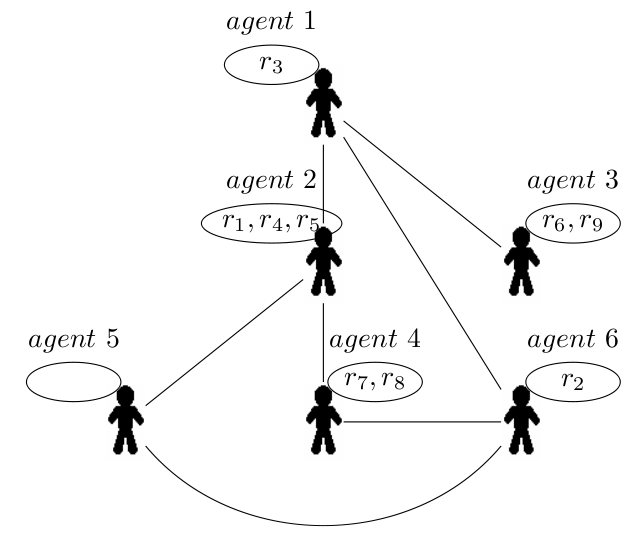
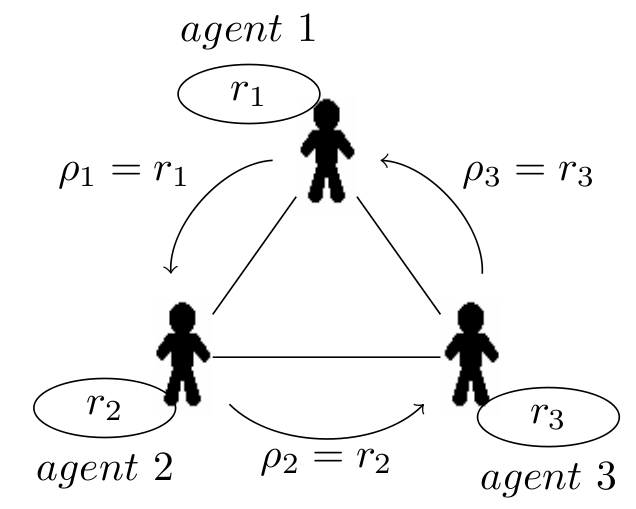
is based its decisions.Example 1 Figure 1 illustrates a negotiation problem based on a population of 6 agents and a set of 9 resources (
is a tuple
〈Ri, vi, Bi, Ci, Ni〉, where
Ri is the set of mi resources
the agent owns, vi is the valuation function (the
agent preferences), Ni is the list of
ni neighbors, Bi
defines the agent behavior according to which the agent negotiates,
and Ci is its acceptability criterion on which
is based its decisions.Example 1 Figure 1 illustrates a negotiation problem based on a population of 6 agents and a set of 9 resources ( = {1,..., 6},
= {1,..., 6}, 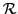 = {r1,..., r9}).
= {r1,..., r9}).
These resources are initially allocated to the agents. Each agent owns a resource bundle and their aggregation constitutes the initial resource allocation, which can be extracted from Figure 1 as follows:
A =According to allocation A, agent 1 only owns r3 while agent 2 owns 3 resources r1, r4 and r5. No resource belongs to agent 5, etc...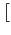 {r3} {r1, r4, r5} {r6, r9} {r7, r8} {} {r2}
{r3} {r1, r4, r5} {r6, r9} {r7, r8} {} {r2}![$\displaystyle \big]$](5/img12.png) .
.
The contact graph describes the interaction possibilities of the agents. Two agents can only communicate if they are directly linked. According to the topology of the contact graph described in Figure 1, we can say that agent 4 is able to negotiate with agents 2 and 6 while agent 3 can only communicate with agent 1.
Considering a centralized technique, the resources and the agent preferences are gathered in a central entity which determines an optimal resource distribution performed afterwards. However, considering a distributed method based on agent negotiations, the solving process proceeds as follows. An agent is selected to be the initiator, agent 1 for instance. It negotiates in its neighborhood by first selecting one neighbor, agent 2 for instance, and then negotiating with it according to its behavior. They both locally determine that the exchange of resources r3 and r5 is acceptable, with respect to their own criterion. This transaction is performed and the resource allocation evolves. A new initiator is selected and the process continues until no more acceptable transaction can be determined.
- 3.9
-
Many applications can be modeled using such a representation. For
instance, home exchange websites which appear on the
Internet. Each customer/agent enters the system with one resource: its
house. They want to exchange their house for another one
during a given time period (for holidays for example). The contact
graph can be built out of the customers requirements. The objective of
such an application is to satisfy a maximum number of customers
without neglecting any of them (every customer who lend their house must
find another one in return). The next section is dedicated to another crucial
model parameter: the evaluation of an allocation from a local and a
global point of view. The importance and the impact of using a contact graph is also discussed.
Individual and collective welfare - 3.10
-
The satisfaction of an agent depends directly on its personal resources. It can be evaluated by a valuation
function considering different parameters more or less
important to the agent.
- 3.11
-
In many studies in the literature, the individual welfare of an agent
(i.e. its satisfaction) only depends on its utility
(Endriss et al., 2006; Chevaleyre et al., 2010; Sandholm, 1998). In such studies, money is introduced during
the transactions. Indeed, transactions are performed if and only if they
satisfy all the conditions imposed by all the agents involved in the
transaction. Money can be used to compensate a disadvantageous
transaction leading to a loss of utility for example. One
constraint only controls the use of money: it prevents the creation of
money during a transaction. In other words, the amount of money given
by an agent (negative value) corresponds to the exact amount of money received by the
other agent (positive value). The sum of compensatory payments of a
transaction must be null. This argument seems consistent and
reasonable. However, it is not sufficient and it leads to unrealistic
situations since the agent wallet is not bounded. An agent is
considered as rich as required to compensate any disadvantageous
transaction. Infinite compensatory payments do not represent a
plausible assumption in most applications. Instead of allowing
infinite compensatory payments, we choose not to consider money and to
restrict the valuation function to a utility function in this
paper.
- 3.12
-
Various representations of agent preferences exist in the literature
(Doyle, 2004; Mas-Colell et al., 1995). In this paper, agents express their preferences
using a cardinal quantitative representation: an additive utility
function.
Definition 5 (Utility function) An agent evaluates its individual welfare using an additive utility function ui : 2
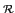 →
→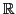 . When agent
i∈
. When agent
i∈ owns a set of
resources
Ri⊆
owns a set of
resources
Ri⊆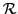 , its utility is
evaluated as follows:
ui(Ri) =
, its utility is
evaluated as follows:
ui(Ri) =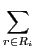 ui(r), i∈
ui(r), i∈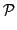 , Ri⊆
, Ri⊆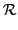 .
Example 2 Let us illustrate the evaluation of the individual welfare using a simple example, based on a population of 3 agents
.
Example 2 Let us illustrate the evaluation of the individual welfare using a simple example, based on a population of 3 agents = {1, 2, 3} and a set of 6 resources
= {1, 2, 3} and a set of 6 resources
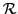 = {r1,..., r6}. The agents
preferences are described in Table 1. According to
this table, agent 1 associates with resource
r2 the utility value:
u1(r2) = 7.
= {r1,..., r6}. The agents
preferences are described in Table 1. According to
this table, agent 1 associates with resource
r2 the utility value:
u1(r2) = 7.
Table 1: Individual Welfare – Agent preferences ui(rj) Resource Set 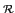
r1 r2 r3 r4 r5 r6 Population 
1 10 7 10 9 2 1 2 6 10 3 4 8 6 3 1 2 1 2 1 3
If the initial resource allocation is A = [{r4}{r1, r2, r6}{r3, r5}], then the utility of all the agents can be easily computed as follows:u1(R1) = u1({r4}) = u1(r4) = 9 u2(R2) = u2({r1, r2, r6}) = u2(r1) + u1(r2) + u2(r6) = 6 + 10 + 6 = 22 u3(R3) = u3({r3, r5}) = u3(r3) + u3(r5) = 1 + 1 = 2 - 3.13
-
The individual welfare is the evaluation of an allocation from an
agent point of view thanks to its utility function. The quality of an
allocation must be evaluated from a global point of view. In this
purpose, notions from the social choice theory are usually used
(Moulin, 1988; Arrow et al., 2002). These notions aggregate the satisfaction of all
agents in the population to evaluate an allocation. In this paper, we
focus on the four most important notions.
- 3.14
-
The most widely used notion is the utilitarian welfare, which optimizes
the average satisfaction in a population.
Definition 6 (Utilitarian welfare) The utilitarian welfare of a resource allocation A corresponds to the sum of individual welfare.swu(A) =
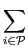 ui(Ri), A∈
ui(Ri), A∈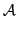 .
.
- 3.15
-
The egalitarian welfare of an allocation corresponds to the individual
welfare of the poorest agent in the population. Its maximization tends
to reduce inequalities in the societies.
Definition 7 (Egalitarian welfare) The egalitarian welfare of an allocation A corresponds to the individual welfare of the poorest agent.swe(A) =
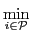 ui(Ri), A∈
ui(Ri), A∈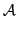 .
.
- 3.16
-
The Nash product considers the average individual welfare and the
inequalities within an agent population. This notion can be viewed as
a compromise between the utilitarian and the egalitarian welfare. This
notion is independent of utility scales and it also normalizes the agents
utility. However this notion becomes meaningless if non-positive
values are used.
Definition 8 (Nash product) The Nash product of an allocation A corresponds to the product of individual welfare.swn(A) =
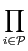 ui(Ri), A∈
ui(Ri), A∈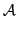 .
.
- 3.17
-
Finally, the elitist welfare only considers the welfare of the richest
agent in the population. This notion can be useful in the context of
artificial societies for instance, where agents have a common
objective. This objective must be fulfilled irrespective of the
agent which achieves it.
Definition 9 (Elitist welfare) The elitist welfare of an allocation A corresponds to the individual welfare of the richest agent in the population.swe
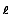 (A) =
(A) = 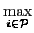 ui(Ri), A∈
ui(Ri), A∈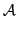 .
.
- 3.18
-
All the basic notions having been presented, we can use them to
discuss the importance of the social graph in the next section.
Importance of the contact graph - 3.19
-
Since only few studies consider restrictions on agent interactions, it
is legitimate to investigate the importance of such a
parameter. Indeed, negotiation processes, which lead to optimal
solutions according to complete communication possibilities (i.e.,
based on complete social graphs), may only lead to solutions far from
the optimum when communications are restricted.
Proposition 1 (Social graph impact) Independently of the objective function considered, a restricted social graph may prevent the achievement of optimal resource allocations.Proof. Let us prove this proposition by a counter-example based on a population
 = {1, 2, 3} and a
set of resources
= {1, 2, 3} and a
set of resources
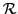 = {r1, r2, r3}. The objective is to maximize the Nash welfare. All the agents are assumed self-interested (they only accept
transactions increasing their own individual welfare). The agent
preferences are described in Table 2 while the
contact graph, which describes the interaction possibilities, is
represented in Figure 2.
= {r1, r2, r3}. The objective is to maximize the Nash welfare. All the agents are assumed self-interested (they only accept
transactions increasing their own individual welfare). The agent
preferences are described in Table 2 while the
contact graph, which describes the interaction possibilities, is
represented in Figure 2.
Table 2: Contact graph impact – Agent preferences ui(rj) Resource Set 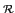
r1 r2 r3 Population 
1 3 1 9 2 1 4 1 3 10 2 3
According to the topology of this social graph, agent 2 can communicate with agents 1 and 3, while they can only communicate with agent 2 but not together. The initial resource allocation is A =
 {r1}{r2}{r3}
{r1}{r2}{r3}![$ \big]$](5/img24.png) and is associated with
swn(A) = 36.
and is associated with
swn(A) = 36.
Two resource swaps (one-for-one resource replacement) only are possible. Agents 1 and 2 can exchange r1 and r2 or agents 2 and 3 can exchange respectively r2 and r3. Both cases lead to a decrease of the utility of at least one participant. Thus, no acceptable exchange is possible here.
However, allocation A is not an optimal solution. Indeed, the swap of r1 and r3 by agents 1 and 3 would lead to a better allocation A' =
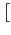 {r3}{r2}{r1}
{r3}{r2}{r1}![$ \big]$](5/img24.png) , which is associated with
swn(A') = 360. Hence, due to the topology of the social
graph restricting the interaction possibilities, the negotiation
process cannot achieve an optimal solution.
, which is associated with
swn(A') = 360. Hence, due to the topology of the social
graph restricting the interaction possibilities, the negotiation
process cannot achieve an optimal solution.

- 3.20
-
Considering the social graph also has an indirect influence on
negotiation processes. While it may not be important to consider the
order in which the agents negotiate when the social graph is complete,
this order becomes essential when communications between agents are
restricted. Indeed, if restrictions on agent communications are not
considered, resources can always be traded with all other agents.
Proposition 2 (Negotiation order) Independently of the objective function considered, the order in which agents negotiate with each other may prevent the achievement of optimal resource allocations.Proof. The proposition can be proved by a counter-example. Let us consider a population
 = {1, 2, 3} of
selfish agents and a set of resources
= {1, 2, 3} of
selfish agents and a set of resources
 = {r1, r2, r3}. The objective is still to maximize
the Nash welfare. The agent preferences are described in Table
3 and the contact graph is illustrated in Figure
2. The initial resource allocation is
A=[{r1}{r2}{r3}] with
swn(A) = 6.
= {r1, r2, r3}. The objective is still to maximize
the Nash welfare. The agent preferences are described in Table
3 and the contact graph is illustrated in Figure
2. The initial resource allocation is
A=[{r1}{r2}{r3}] with
swn(A) = 6.
Let us now assume that agent 2 initiates a negotiation. According to the topology, two partners are possible. Depending on the choice of the initiator, the negotiation process may end on a sub-optimal allocation. Indeed, if agent 2 negotiates first with agent 1, the allocation achieved is A' = [{r2}{r1}{r3}] with swn(A') = 50. However, if agent 3 is chosen first, the allocation achieved is A'' =
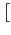 {r1}{r3}{r2}
{r1}{r3}{r2}![$ \big]$](5/img24.png) with
swn(A'') = 126.
with
swn(A'') = 126.
Hence, the order of negotiation becomes an important parameter to consider when the interaction possibilities are restricted.

- 3.21
-
In this section, we have shown the importance of considering restricted
communication abilities, as it occurs in many applications. These
restrictions represent more plausible assumptions but they also have
important consequences for the negotiation efficiency. The topological
characteristics may prevent the achievement of optimal
solutions. Moreover, the order in which agents negotiate may also lead
negotiation processes to sub-optimal allocations. In spite of their
respective impact, these two parameters have not been considered so far. The context of many former studies can be considered as ideal
while ours is more realistic.
- 3.22
-
A negotiation process between agents changes an initial resource
allocation to an optimal one using local transactions. Agents only
accept transactions that satisfy their acceptability criterion. When
no agent is able to find an acceptable transaction with respect to its
behavior then the negotiation process is considered as over. The next
section describes the transactions and the different acceptability criteria.
Transactions and acceptability criterion - 3.23
-
During a negotiation process, the resource allocation evolves step by
step by means of local transactions between agents. The resource traffic
is generated by these transactions as they move resources
successively from the bundles of one agent to another. Transactions can be
classified in two main families (Sandholm, 1998): multilateral
transactions where many agents can be involved simultaneously and
bilateral transactions where only two agents at a time can
trade resources. Although a few studies are dedicated on multilateral
transactions (Endriss & Maudet, 2005), no algorithm exists to determine them in a
scalable way. Consequently, only bilateral transactions are
considered in this paper.
- 3.24
-
Two agents at a time are involved in bilateral transactions: an
initiator and its partner. Bilateral transactions can be characterized
by the number of resources that both participants can propose. Thus,
it can be defined in a generic way as follows:
Definition 10 (Bilateral transactions) A bilateral transaction between two agents i, j∈A transaction δ transforms an initial allocation A into a new allocation A'. Different notations exist in the literature to express such an evolution using the state of the system before and after the transaction, like δ = (A, A') for instance. All bilateral transactions classified in (Sandholm, 1998) can be represented using the model presented in Definition 10. For instance, a 〈1, 0〉-transaction corresponds to a gift (also called O-contract): the initiator gives a unique resource without counterpart.
 , denoted by
δij, is initiated
by agent i and involves a partner agent j. It is a
pair
δij〈u, v〉 = (ρi, ρj), where the initiator
i offers a set
ρi of u resources and
its partner j offers a set
ρj of v
resources.
, denoted by
δij, is initiated
by agent i and involves a partner agent j. It is a
pair
δij〈u, v〉 = (ρi, ρj), where the initiator
i offers a set
ρi of u resources and
its partner j offers a set
ρj of v
resources. - 3.25
-
The complexity of a negotiation between two agents is significantly affected
by the maximum number of resources the agents are willing to offer.
Proposition 3 (Bilateral complexity) The number of possible bilateral transactions between two agents i, j∈
 where exactly u and v resources can be respectively offered is:
#δij =
where exactly u and v resources can be respectively offered is:
#δij =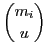 ×
×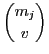 .
.
- 3.26
-
The kinds of transaction allowed during a negotiation, denoted by
Δ, define a negotiation policy. For instance, the agents
may also be allowed to offer resources in a transaction up to a specified amount. Let us
call ''up to
〈2, 2〉'' the negotiation policy according
to which the agents can offer either nothing, one or two resources. The
kinds of transaction allowed can be written explicitly as:
"up to {〈2, 2〉}"⇔Δ = {〈x, y〉| x≤2, y≤2}Proposition 4 (Complexity of Negotiation policy) If the two agents i, j∈
 are allowed
to offer up to u' and v' resources (
u'≤mi, v'≤mj) then the number
of possible bilateral transactions between them is:
#δij =
are allowed
to offer up to u' and v' resources (
u'≤mi, v'≤mj) then the number
of possible bilateral transactions between them is:
#δij =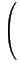
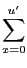
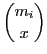
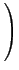
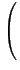
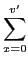
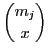
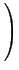 - 1.
Proof. A negotiation policy is defined based on the number of resources an agent can offer. If an agent can offer up to three resources then it can offer any subset of his bundle containing at most three resources.
- 1.
Proof. A negotiation policy is defined based on the number of resources an agent can offer. If an agent can offer up to three resources then it can offer any subset of his bundle containing at most three resources.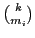 represents the
possible number of offers containing exactly k resources that
agent i can propose (according to the number of resources
it owns mi). The total number of offers an
agent can propose can be computed by a simple summation of such
terms. Once the number of offers has been computed for each agent,
determining the possible number of transactions between them is
trivial.
represents the
possible number of offers containing exactly k resources that
agent i can propose (according to the number of resources
it owns mi). The total number of offers an
agent can propose can be computed by a simple summation of such
terms. Once the number of offers has been computed for each agent,
determining the possible number of transactions between them is
trivial.
 Example 3 For instance, let us consider two agents i, j∈
Example 3 For instance, let us consider two agents i, j∈ involved in a negotiation initiated by agent
i. These agents own bundles of respectively 10 and 20
resources. Let us determine the possible number of transactions
according to different negotiation policies.
involved in a negotiation initiated by agent
i. These agents own bundles of respectively 10 and 20
resources. Let us determine the possible number of transactions
according to different negotiation policies.
Δ = {〈1, 0〉} ⇒ #δij = 10 Δ = {〈1, 1〉} ⇒ #δij = 199 Δ = {〈x, y〉| x≤2, y≤2} ⇒ #δij = 40500
When only gifts from the initiator are allowed, 10 transactions are possible since the agent owns 10 resources only. When swaps only are allowed, both participants offer one unique resource. Thus, 200 different transactions are possible. However, when participants can offer up to two resources from their bundle, the number of possible transactions explodes up to 40,500. According to the kinds of transaction allowed, a negotiation can quickly become unscalable. Restricting the cardinality of the allowed transactions is thus essential to guarantee the scalability of the solving method. - 3.27
-
In a distributed environment where agents have only access to local information,
the finiteness of the solving process is essential. It can be
guaranteed by the use of a proper acceptability criterion, enabling the agents to locally determine the profitability of a transaction. When no agent is able to find an acceptable transaction
in its neighborhood, the negotiation process stops. The most widely
used criterion is the individual rationality
(Camerer, 2003; Sandholm, 1998; Montet & Serra, 2003). Since no
compensatory payment is allowed, a rational agent only accepts
transactions that increase its individual welfare. This notion can be
defined as follows:
Definition 11 (Individually rational agent) A rational agent accepts only transactions δ which change an initial allocation A into another one A' while increasing its individual welfare:In (Endriss et al., 2006), the notion of cooperative rationality has been introduced. The authors proved that any sequence of cooperative rational transactions leads to Pareto optimal allocations. However, Pareto optimal allocations can be far from socially optimal allocations. Moreover, the notion of cooperative rationality cannot be used easily in practice. Indeed, a weak inequality may lead to a cycle of transactions between equivalent allocations, which can prevent the convergence of the negotiations. Thus, the negotiation processes between cooperative rational agents may not be finite.ui(Ri') > ui(Ri), i∈
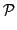 .
.
- 3.28
-
The individual rationality guarantees that the welfare of each agent
is increased by each transaction. However, from the point of
view of the society, negotiations between individually rational agents may also lead
to severely sub-optimal allocations. As a consequence, a different acceptability
criterion should be used to achieve better allocations society-wise. We
propose the notion of social agents which are willing to accept transactions
that decrease their individual welfare as long as they favor the welfare of the whole
society.
Definition 12 (Social agent) A social agent only accepts transactions δ(A) = A' that do not penalize the whole society.sw(A)≥sw(A'), A, A'∈
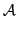 .
.
- 3.29
-
This definition is close to the definition of individually rational
agents in (Endriss et al., 2006) when compensatory payments are
allowed. However, the different context leads to drastic changes in
its practical use. Firstly, this criterion is based on global
knowledge which is not available at the agent level (the resource
allocation). Secondly, the use of a weak inequality may lead to infinite
negotiation processes like in the case of collaborative
rationality described previously.
- 3.30
-
The formal definition of this social acceptability criterion is based
on global information. However, we assume that the knowledge of the agents is
restricted to their own preferences, their own bundle or information that can be collected during a negotiation (from related agents involved in the current transaction only). That way, an agent is
neither aware of the current resource assignment nor of the population
size and the preferences of the other agents. Consequently, an agent does not have enough
information to determine the social welfare value, although computing
the social welfare value is not essential. Indeed, an agent merely needs
to know whether the transaction increases or decreases the social welfare value. The expression of the social acceptability criterion can be restricted to the transaction participants. Of
course, the formula of the acceptability criterion must be adapted
with respect to the social notion considered, as described
in the next paragraphs. These restricted criteria are strict inequalities in order to
guarantee the finiteness of the negotiation processes.
Utilitarian sociability - 3.31
-
Social agents accept transactions that do not harm the society, even if they
decrease their individual welfare. Let us adapt the generic formula to
the specific case of utilitarian societies (Nongaillard et al., 2008). An
utilitarian transaction
δij = (ρi, ρj), which transforms A
in
A'(A, A'∈
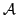 ), must
satisfy the following condition:
), must
satisfy the following condition:
swu(A) < swu(A') ui(Ri) + uj(Rj) + 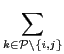 uk(Rk)
uk(Rk)< ui(Ri') + uj(Rj') + 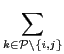 uk(Rk')
uk(Rk')ui(Ri) + uj(Rj) < ui(Ri') + uj(Rj') ui(Ri) + uj(Rj) < ui(Ri) + ui(ρj) - ui(ρi) + uj(Rj) + uj(ρi) - uj(ρj) ui(ρi) + uj(ρj) < ui(ρj) + uj(ρi)
In other words, if the partner associates a larger utility value with the resources offered than the initiator, then the transaction is profitable to the society. Each utilitarian transaction leads to a strict increase of the welfare of the society (if utility values are not null). Note that the utilitarian interpretation of the social acceptability criterion is only based on the resources offered. The initial individual welfare of the participants does not affect the acceptability of a transaction.
Egalitarian sociability - 3.32
-
In the case of an egalitarian society, transactions reduce inequalities
between agents. A fair transaction
δij = (ρi, ρj), which transforms A
in
A'(A, A'∈
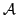 ), must
satisfy the following conditions:
), must
satisfy the following conditions:
swe(A) ≤ swe(A') 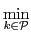
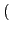 uk(Rk)
uk(Rk)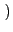
≤ 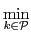
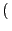 uk(Rk')
uk(Rk')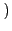
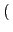 ui(Ri), uj(Rj)
ui(Ri), uj(Rj)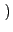
< 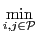
 ui(Ri'), ui(Rj')
ui(Ri'), ui(Rj')
The poorest agent after a fair transaction must be richer than the poorest agent before the transaction. When the egalitarian welfare is considered, an increase of the welfare value cannot be guaranteed. Indeed, depending whether or not the poorest agent is involved in the transaction, the egalitarian welfare value may not be increased. If the poorest agent is not involved, its utility value, which corresponds to the egalitarian welfare value, does not vary since its resource bundle is not modified. Thus, the egalitarian welfare value only changes if the poorest agent of the population is involved. In contrast to the utilitarian acceptability criterion, which only depends on the traded resources, the egalitarian interpretation is based on the sets of traded resources as well as on the initial individual welfare of each participant. According to such a criterion, a very rich agent may accept to decrease its own utility for the benefit of the whole society. In the case where the poorest agent is not involved in a transaction, the egalitarian criterion favors the resource traffic.
Nash sociability - 3.33
-
The Nash welfare can be viewed as a compromise between the utilitarian
and the egalitarian notions. The Nash interpretation of the
social acceptability criterion also combines the characteristics of
both notions (Nongaillard et al., 2010; Nongaillard et al., 2009). A Nash
transaction
δij = (ρi, ρj), which transforms A
in
A'(A, A'∈
 ), must
satisfy the following condition:
), must
satisfy the following condition:
swn(A) < swn(A') 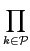 uk(Rk)
uk(Rk)< 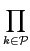 uk(Rk')
uk(Rk')ui(Ri)uj(Rj) 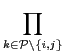 uk(Rk)
uk(Rk)< ui(Ri')uj(Rj') 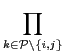 uk(Rk')
uk(Rk')ui(Ri)uj(Rj) < ui(Ri')uj(Rj')
Each Nash transaction strictly improves the welfare of the society, like in utilitarian transactions. Similarly to the egalitarian interpretation of the social acceptability criterion, the Nash criterion must be based on traded resources as well as on the individual welfare of both participants.
Elitist negotiations - 3.34
-
Elitist agents accept transactions
δij = (ρi, ρj), changing A into
A'(A, A'∈
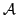 ), if the
following condition is satisfied:
), if the
following condition is satisfied:
swe 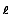 (A)
(A)< swe  (A')
(A')
 uk(Rk)
uk(Rk)
≤ 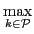
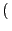 uk(Rk')
uk(Rk')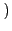
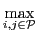
 ui(Ri), uj(Rj)
ui(Ri), uj(Rj)
< 
 ui(Ri'), ui(Rj')
ui(Ri'), ui(Rj')
The richest of the two participants after an elitist transaction must be richer than the richest agent before this transaction. Similarly to the egalitarian interpretation, an increase of the elitist welfare value cannot be guaranteed. However, the restriction is not as strong as the restriction imposed in the egalitarian case. Indeed, if the poorest agent of the population is not involved, the egalitarian welfare value cannot vary, but according to the elitist notion, even if the richest agent is not involved, the welfare value can increase. Nothing prevents for instance another agent to become richer than the agent that was the richest before the transaction.
Agent behaviors - 3.35
-
A behavior defines an agent from an external point of view: it describes
how an agent interacts with others, i.e. how they negotiate. A transaction is a
combination of offers from each participant. An agent initiating a negotiation selects a partner from its neighborhood, makes and receives offers and checks their acceptability according to its own
criterion. If a transaction is acceptable for every participant, it is
performed. Otherwise, one agent must modify its offer, in accordance with its
behaviour, and the negotiation continues. The order in which these actions are performed (if they
are) constitutes a behavior.
- 3.36
-
Many behaviors have been implemented and tested but only the most
efficient (according to the quality of the solutions achieved) is
presented here (Nongaillard et al., 2008). Our experiments show that
agents should be able to change their offers and partners. Such a behavior
is more time-consuming than stubborn behaviors (agents refuse to
change their offers) but leads negotiation processes to higher social
welfare values. The order in which the actions are performed according
to a behavior also affects the efficiency of the negotiations. Three
levels of priority can be distinguished: on the partner selection, on
initiator offers and on partner offers. Our experiments show that the
behavior described next is the most efficient.
- 3.37
-
According to the kinds of negotiation policy allowed, each agent can
offer up to a maximum number of resources. Doing so, they generate a list of the offers they can make according to their preferences and they sort it. Agents always propose the least penalizing offer
first. In this behavior called frivolous flexible, described in
Algorithm 1, the offer and the partner can be changed by the initiator during a negotiation. Each offer is proposed to every neighbor by the initiator first of making a concession and modifying the offer.
- 3.46
-
Note that when the utilitarian welfare is considered, the
three priorities do not affect the results. Indeed, different
negotiation processes will lead to equivalent solutions. However, when
other welfare notions are considered, these priorities, which define
the order of the actions, can lead to suboptimal allocations.
 Simulation results
Simulation results
- 4.1
-
This section starts with detailing how negotiation processes are evaluated, presenting the metrics used and their role. Then, the experimental protocol is described to present what simulations have been
performed. Only simulations related to utilitarian and egalitarian
societies are analyzed in the next sections.
Evaluation metrics - 4.2
-
In this experimental study, different aspects of negotiation processes
are evaluated by to three main parameters.
- 4.3
-
The first parameter is the transaction cardinality. Identifying
an acceptable bilateral transaction may become a complex and expensive
task if large numbers of resources can be traded at once, as described
in Section 3.4. In order to favor the scalability of
our method, restrictions on the transaction cardinality are
essential. However, such restrictions may affect the efficiency of
negotiation processes. The aim is to determine if the use of large
transactions is necessary to achieve socially interesting allocations.
- 4.4
-
The second parameter we use to evaluate negotiation processes is
the social efficiency. Although resource allocation problems
can be solved using a centralized framework, a solution
provided by such a technique merely allocates the resources optimally, without considering the transaction sequence required to achieve it. Such approaches cannot handle restricted
graphs in a scalable way. An omniscient central entity gathers every
information, from bundles to agents preferences, in order to
determine the optimal outcome. Social welfare values provided by such
centralized techniques can be used as references to evaluate the
absolute efficiency of our distributed mechanism. The centralized
techniques used to estimate the optimal value are described at the
beginning of each result section.
- 4.5
-
The topological characteristics of a contact graph have a direct impact on the
efficiency of negotiation processes. For this reason, contact graphs from different
classes are considered in order to evaluate the negotiation processes
on representative graphs. We focus on a specific parameter: the
mean connectivity. The mean connectivity corresponds to the
average number of neighbors per agent and therefore represents the density of
the contact graph. The aim is here to determine the size of the
neighborhood required to achieve socially efficient allocations.
Simulation protocol - 4.6
-
Having defined how negotiation processes are evaluated, let us now
describe how the simulations are performed.
- 4.7
-
Each experiment is set up as follows. An artificial society is composed of 50 agents (n = 50) and 250 resources (m = 250) spread between them. Two types of structured graph (complete and
grid) and two types of random graph (Erdős-Rényi 1959) and small world (Albert & Barabási
2002) are considered.
First of starting the experiment, a large number of scenarios are generated: 10 graphs of each class and 10 sets of agent preferences.
Then, 100 simulations are performed from different initial allocations for each scenario (couple
preference + graph).
Two acceptability criteria are considered during the simulations: the individual rationality and the sociability. Four negotiation policies are considered in each case: two allowing only
one type of transaction (gifts and swaps) and two allowing several
types of transaction (''up to
〈1, 1〉'' and ''up to
〈2, 2〉''). Since gifts cannot be individually rational,
some negotiation policies do not exist in societies of individually rational agents.
- 4.8
-
The resources are initially distributed randomly. The preferences are
also generated randomly in the range {1..m}. For
experiments focusing on connectivity, only Erdős-Rényi graphs are used and the
probability p for a link to exist between two agents varies from
0.05 to 1. During a negotiation process, the initiator agent is
randomly chosen and the speech turn is uniformly distributed: no agent
can talk twice before all the others talked at least once. When no
one is able to find an acceptable transaction, the negotiation process
ends.
- 4.9
-
The size of the scenarios (50 agents and 250 resources) used for the
simulations may seem light in contrast with the claimed scalability of our approach.
Yet, only a few studies in the literature include
experiments, most of them being purely theoretical. Among the experimental
studies, the number of agents is often
restricted to less than 10, with a maximum of 20 resources
(Estivie et al., 2006; Ramezani & Endriss, 2009; Chevaleyre et al., 2007; Andersson & Sandholm, 1998), which is far beyond our parameters.
Also, we choose to evaluate the social efficiency. In this purpose, the optimal
social value, which is estimated owing to centralized techniques, is used as a reference for comparisons. The complexity of allocation problems is exponential with respect to the population size and to the
size of the resources set. Besides, the estimation of the optimal value according to
these centralized techniques is very time-consuming. For this reason, the comparison
with the estimation of the optimal results is the main limiting factor
to the size of our experiments.
 Utilitarian negotiations
Utilitarian negotiations
-
Impact of the transaction cardinality - 5.1
-
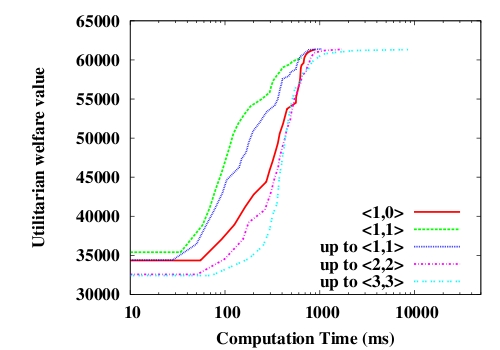
Figure 3 shows the impact of the
transaction cardinality on negotiation processes within utilitarian
societies. It represents the evolution of the utilitarian welfare
value in function of the computation time. The efficiency of different
negotiation policies, classified with respect to the maximum number of
resources proposed by the agents, can also be compared. The best
negotiation policy leads to the largest social welfare
value in a minimum time.
Figure 3 shows that, independently of the cardinality of the allowed transactions, all negotiation processes converge towards very close utilitarian welfare values whereas the computation time required for the convergence quite varies. The negotiation policy based on gifts ( 〈1, 0〉 transactions) leads to a faster convergence towards the largest welfare value. Larger bilateral transactions do not allow the achievement of higher utilitarian allocations although they are more time consuming. Negotiation processes based either on gifts ( 〈0, 1〉 transactions), swaps ( 〈1, 1〉 transactions) or both end after about 1 second while 10 seconds are required in the case of the negotiation policy ''up to 〈3, 3〉'' for instance. Negotiation processes based on swaps end on socially weaker allocations. Since the initial resource distribution cannot be modified, negotiation processes based on swaps end on weaker local optima. The improvement of the welfare value is quicker when agents negotiate either using ''up to 〈1, 1〉'' or 〈1, 1〉 transactions. It can represent an interesting alternative if a good approximation is required in a short time. However, it strongly depends on the mean number of resource per agent. In these experiments, agents own an average of 5 resources in their bundle but larger resource bundles affect the convergence speed. Indeed, larger resource bundles mean a higher number of possible transactions between each pair of agents, and thus lead to a decrease in gradient of the corresponding curves.
Proposition 5 (Utilitarian bilateral transaction decomposition) Any bilateral transaction satisfying the utilitarian criterion can be decomposed into a sequence of utilitarian gifts leading at least to a socially equivalent allocation.Proof. Let us consider a bilateral transaction between two agents i, j∈ changing the initial
allocation A into A'. It can be formulated
by definition as follows:
changing the initial
allocation A into A'. It can be formulated
by definition as follows:
δij〈X, 0〉 = (ρi,∅) is social ⇒ swu(A) < swu(A').
Two cases can occur.- All the resources offered by the initiator are more valued by the partner.
∀r∈ρi, ui(r) < uj(r) ⇒ ∀r∈ρi, δij〈1, 0〉 = (r,∅) is social.
In such a case, the decomposition of the initial transaction δij〈X, 0〉 = (ρi,∅) into a sequence of social 〈1, 0〉-transactions leading to the same allocation is trivial. - The initiator values (at least) one resource from its offer
more than the partner involved. In such a case, the transaction
cannot be split into a sequence of utilitarian gifts. However,
this transaction is suboptimal. There exists a transaction of
lesser cardinality leading to a socially more interesting
allocation A''.
∃r∈ρi, ui(r) < uj(r) ⇒ δij〈X - 1, 0〉 = (ρi  {r},∅) is social.
{r},∅) is social.and swu(A'') > swu(A') > swu(A).
Indeed, removing from the initiator's offer all the resources less valued by the partner constitutes a new transaction leading to a socially greater allocation A''.swu(A'') = swu(A) - 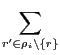 ui(r') +
ui(r') + 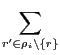 uj(r')
uj(r')= swu(A') + ui(r) - uj(r) > swu(A')

- All the resources offered by the initiator are more valued by the partner.
- 5.2
-
Since the utilitarian welfare value achieved is similar regardless of the transaction cardinality, the use of large bilateral transactions is not justified due to important additional
costs. Besides, restrictions on the transaction cardinality do not harm the
efficiency of negotiation processes.
Utilitarian efficiency - 5.3
-
In order to determine the social efficiency of negotiation processes,
the optimal social value must be computed according to a centralized
technique. In the context of this study, the optimal utilitarian
welfare value can be determined using Algorithm
2.
- 5.4
-
Table 4 presents the efficiency of
negotiation processes based on different negotiation policies, acceptability criteria and classes of contact
graph. This table shows the proportion of the optimal welfare value
that can be achieved (the greater the proportion, the more
efficient the negotiation process).
Table 4: Utilitarian efficiency (%) according to the class of graphs Graph
SocialNegotiation policy Rational Social 〈1, 1〉 up to 〈2, 2〉 〈1, 0〉 〈1, 1〉 up to 〈1, 1〉 up to 〈2, 2〉 Full 96.6 97.0 100 98.3 100 100 Grid 79.0 81.3 86.2 85.3 86.1 86.1 Erdős-Rényi 94.8 95.0 98.9 97.1 98.9 98.9 Small world 80.8 84.8 91.4 90.0 90.2 90.3
- 5.5
-
When considering complete graphs, different negotiation policies
always lead to optimal resource allocations. The transactions of
weakest cardinality, which achieve optimal allocations, are social
〈1, 0〉 transactions (social gifts). Any negotiation
policy that includes social gifts, like ''up to
〈1, 1〉'', ''up to
〈2, 2〉'' or ''up to
〈3, 3〉'' also achieves socially optimal resource
allocations. However, their use leads to important additional
costs. The use of social gifts is sufficient to achieve optimal
allocations when the utilitarian welfare is considered. Table
4 also shows that, independently of the
social graph class, rational negotiation processes always lead to
socially weaker allocations than social negotiation processes. The
restrictive character of the acceptability criterion affects the
resource circulation and consequently the quality of the provided
solution. We can observe that agents in an artificial society must
be able to give resources without counterpart. Negotiation policies
that exclude such actions, i.e. if gifts are forbidden or never
considered as acceptable, lead to socially weaker results. Generosity
between the agents of the population is an essential characteristic to
achieve an optimal allocation in utilitarian societies.
Theorem 6 Within an utilitarian society where agents express their preferences by means of additive utility functions, negotiation processes based on complete social graphs always converge towards a global optimum using only social 〈1, 0〉 transactions.Proof. Since the contact graph is fully connected, any agent i∈
 can communicate with every other agent
j∈
can communicate with every other agent
j∈
 {i}. If a social
〈1, 0〉 transaction containing r can be performed
between agents i and j, then
uj(r) > ui(r)
according to the definition of a social transaction. It is always
possible to create a sequence of social
〈1, 0〉
transactions moving a resource into the bundle of an agent that
associates the largest utility value with it. Applying this process
to each resource, the resulting allocation is always a global
optimum.
{i}. If a social
〈1, 0〉 transaction containing r can be performed
between agents i and j, then
uj(r) > ui(r)
according to the definition of a social transaction. It is always
possible to create a sequence of social
〈1, 0〉
transactions moving a resource into the bundle of an agent that
associates the largest utility value with it. Applying this process
to each resource, the resulting allocation is always a global
optimum.

- 5.6
-
The more restrictions on a contact graph, the less efficient
the negotiations. The combination of a restricted graph like a
grid and the use of rational swaps, which significantly restrict the transaction
possibilities (since initial resource distributions cannot be
modified), leads to the worst social efficiency: Only 79% of the
optimal welfare value can be achieved. When grids are considered,
social negotiation processes achieve up to 86.2% of the optimum. The
weak mean connectivity handicaps the resource traffic and hence the
achievement of socially efficient allocations. Negotiation processes
lead to allocations associated with up to 98.9% of the optimal
welfare value when Erdős-Rényi graphs (p = 0.5) are considered. Only 91.4% of
the optimum is achieved when small-worlds are considered. In an Erdős-Rényi
graph, the probability for an edge to link any pair of nodes
is always the same, while in small-worlds, the probability to link one agent is proportional to the number of agents in its neighborhood. Many agents only have one neighbor and the resource traffic is
unequally distributed. Therefore, bottlenecks (i.e. agents that block the
resource circulation) may appear. Swaps are the least efficient
transactions, but the difference is generally small. Since the number
of resources per agent cannot vary, the resource circulation is very
limited.
Influence of the social graph connectivity
- 5.7
-
The topology of the contact graph affects the resource traffic as well
as the negotiation efficiency. Large agent neighborhoods correspond to
dense contact graphs which facilitate the circulation of the
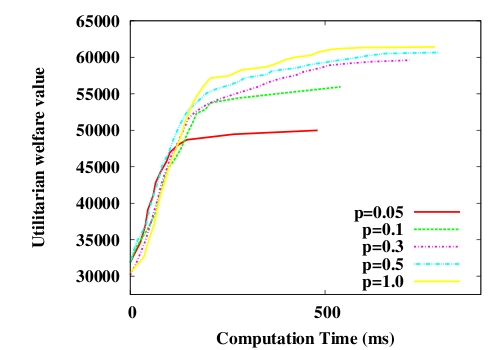
resources. Figure 4 shows the impact of
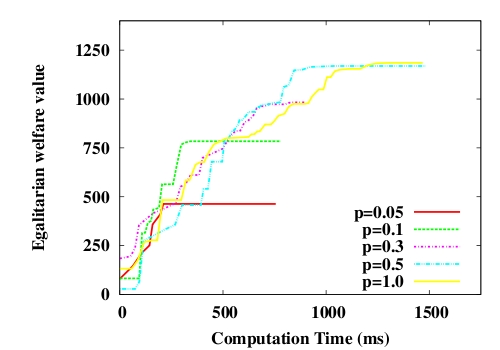
the mean connectivity on the negotiation processes efficiency. It
represents the evolution of the utilitarian welfare value in function of the computation time. Only social gifts are allowed between agents.
This figure shows that a weak probability (which corresponds to small agent neighborhoods) leads utilitarian welfare values to be far from the optimum. For instance, when p = 0.05 the negotiations stop after about 0.5 second although ending on allocations socially far from the optimum. The gradual increase of the probability p leads to longer transaction sequences, to the achievement of greater utilitarian welfare values and to more time-consuming negotiations. Larger neighborhoods facilitate the resource circulation by offering a larger number of possible transactions to all the agents. The impact becomes really significant when p < 0.3. Above this value, the resource circulation is sufficient to achieve socially interesting allocations, yet below this threshold social graphs are too restricted and the flexibility of the social acceptability criterion cannot compensate the restrictiveness of the graph topologies.
 Egalitarian negotiations
Egalitarian negotiations
Influence of the transaction cardinality- 6.1
-
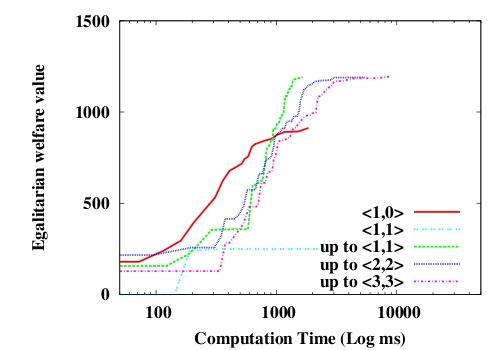
Figure 5 shows the influence of the
transaction cardinality on the evolution of the egalitarian welfare
value during the negotiation processes.
- 6.2
-
Figure 5 shows first that egalitarian
negotiations are much more time-consuming compared to utilitarian negotiations. It
also shows that three negotiation policies lead to similar welfare
value but different convergence times, while two other negotiation
policies achieve weaker results. Indeed, the negotiation policies ''up
to
〈1, 1〉'', ''up to
〈2, 2〉'' and ''up
to
〈3, 3〉'' achieve similar social values but are
respectively more and more time consuming. The negotiation policy ''up
to
〈1, 1〉'', which is included in the two others, is
the simplest policy associated with the best efficiency. The other
negotiation policies lead to useless additional costs that do not
improve the fairness of the artificial society. Several floors can be
observed in the evolution of the egalitarian welfare value. These
floors characterize specific negotiation periods during which the
poorest agent of the population is not involved in the performed
transactions, as described previously in Section
3.4.2. Negotiation processes based on social gifts end
quickly. However, provided solutions are associated to social values
far from the values achieved by larger bilateral transactions. Negotiation processes based on social
〈1, 1〉 transactions (social swaps) require a large number of
performed transactions, which barely improves the social welfare value
and ends on socially very weak allocations. Since such processes are
time consuming and inefficient, the exclusive use of swaps should be
avoided. Using a set of allowed transactions larger than
Δ = {〈1, 0〉,〈1, 1〉} is pointless since it leads to additional costs without any significant improvement on the solution quality. The set of allowed transactions
must be larger when fair artificial societies are considered than in
the case of utilitarian population.
Egalitarian efficiency - 6.3
-
In order to determine the social efficiency of negotiation processes,
the optimal egalitarian value must be computed relying on a
centralized technique. However, there does not exist a simple algorithm like in the case of utilitarian societies. Egalitarian resource allocation
problems can be formulated by means of a mathematical model and solved
using a linear program solver for instance. Our model is based on
Boolean variables describing the ownership of a resource by an agent:
xir = 1 if resource r belongs to agent i, xir = 0
otherwise. Egalitarian resource allocation problems can thus be
written as follows:
sweopt =The objective is the maximization of the poorest agent welfare. Two consistency constraints are also defined. The first ensures that each resource is allocated to a single agent while the second specifies that all resources are atomic, unique and not shareable. Such a technique can estimate the optimal egalitarian value but is very time-consuming.
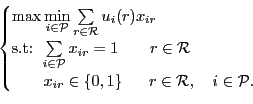
- 6.4
-
Table 5 shows the impact of the
graph topology on the egalitarian negotiation efficiency.
Table 5:Egalitarian negotiation efficiency (%) according to the class of graphs Graph
SocialNegotiation policy Rational Social 〈1, 1〉 up to 〈2, 2〉 〈1, 0〉 〈1, 1〉 up to 〈1, 1〉 up to 〈2, 2〉 Full 19.3 20.8 78.5 24.1 99.9 99.9 Grid 13.9 14.6 66.2 23.6 80.2 80.6 Erdős-Rényi 17.4 20.2 77.3 23.8 96.1 96.6 Small world 13.1 13.9 63.8 23.4 78.1 78.2
Table 5 shows that generally, negotiations among rational agents achieve unfair allocations. Indeed, independently of the kinds of allowed transactions and of the social graph topology, rational negotiation processes end far from the optimal welfare value. Only 20% of the optimal welfare value is achieved in the best cases. The individual rationality, which is widely used in the literature, is not an efficient acceptability criterion. Even on complete graphs, no social negotiation policy can guarantee the achievement of egalitarian optima. Whereas social gifts are well adapted to the solution of utilitarian problems, they do not suit the negotiations within egalitarian societies. Only 78.5% of the optimum can be achieved in the best cases. Indeed, after a finite number of transactions, agents can not give a resource without becoming poorer than their partners were initially. The exclusive use of gifts is then not sufficient to lead negotiations to socially efficient resource allocations. Negotiations based only on social swaps lead to severely sub-optimal resource allocations with an efficiency of 24.1% on complete social graphs in the best case. Such a weak efficiency is mainly due to the inherent constraints of swap transactions. Since the resource distribution cannot be modified, a poor agent who only has few resources initially penalizes a lot the egalitarian negotiation process. When both gifts and swaps are allowed, the negotiation efficiency is really close to the optimum. Larger bilateral transactions bring a small improvement on the fairness among agents but are much more expensive to determine.
Theorem 7 Within an egalitarian society where agents express their preferences by means of additive utility functions, bilateral transactions cannot guarantee the achievement of an egalitarian optimum, independently of the social graph considered.Proof. Let us consider a counter-example, based on a population of three agents = {1, 2, 3} and a set
of three available resources
= {1, 2, 3} and a set
of three available resources
 = {r1, r2, r3}. The agent preferences are described in Table
6.
= {r1, r2, r3}. The agent preferences are described in Table
6.
Table 6:Insufficiency of bilateral transactions in egalitarian negotiations – Agent preferences ui(rj) Resource Set 
r1 r2 r3 Population 
1 2 1 5 2 5 2 1 3 1 5 2
The complete social graph is described in Figure 6 with the initial resource allocation A = [{r1}{r2}{r3}].
This figure also describes the only egalitarian transaction that would be acceptable. No sequence of acceptable bilateral transactions can lead to an optimal resource allocation. Six gifts are possible but none can be performed since they are not social. Indeed, if an agent gives a resource, its bundle becomes empty and the egalitarian welfare value becomes null. Three swaps are possible, but for each the welfare value decreases, which means that the transaction is not acceptable. Hence, even if the multiagent system is completely connected, the optimal solution cannot be achieved using only bilateral transactions. Only a multilateral transaction corresponding to three simultaneous gifts is acceptable as described in Figure 6. Since bilateral transactions are not sufficient when negotiations are based on a complete social graph, they are also not sufficient when the social graph is restricted. In such cases, less transactions are possible and unacceptable transactions on a complete social graph are still unacceptable on a restricted social graph.
- 6.6
-
Graphs of weaker mean connectivity like grids lead negotiation
processes to socially weaker allocations. In the case of small worlds,
many agents only have a few neighbors, which may penalize egalitarian
negotiations. Indeed, if such agents cannot identify an acceptable
transaction with their unique neighbor, some resources may be trapped in
their bundle.
Impact of the contact graph connectivity
- 6.7
-
Figure 7 presents the impact of the
mean connectivity on negotiations within egalitarian societies.
Similarly to utilitarian negotiations, this figure shows that a high probability (corresponding to a dense social graph) leads to longer sequences of transactions during negotiation processes, moreover achieving a higher welfare value. Larger neighborhoods facilitate the resource circulation by offering larger numbers of possible transactions to all agents. The impact of the connectivity is important provided the probability p of generating edges is very low. Like in negotiations on utilitarian societies, the impact of the connectivity is not linear: it becomes really significant below p≤0.5. Societies require a denser contact graph to achieve interesting allocations when fairness is considered.
 Conclusion
Conclusion
- 7.1
-
A large variety of applications can be modeled as resource reallocation problems. Yet, studies investigating such problems do not always consider an adequately realistic context.
Considering that neither omniscient agents nor unrestricted interaction
possibilities represent a realistic environment, the knowledge of the agents in our approach is limited to local information and their possible interaction is defined by a contact graph.
Compensatory payments are also prohibited in order to avoid infinite agent wallet.
- 7.2
-
We also consider that centralized techniques are not best suited for searching transaction sequences leading to an optimal allocation. Therefore, we focus in this paper on distributing solving methods based on agent negotiations.
We seek to define the optimal behavior maximizing the welfare of the whole society. To that end, we propose the agent behavior and the negotiation policy allowing the achievement of socially optimal allocations according to different welfare functions.
The finiteness of the negotiation processes is guaranteed
by an acceptability criterion enabling the agents to determine the
profitability of a transaction on a local basis. In this paper, we
show that negotiations between individually rational agents do not
lead to socially interesting allocations. We propose a new criterion, sociability, that certifies that agents accept any transaction that do not harm the society. The expression of this social acceptability criterion is detailed according to the four main
welfare notions. The agent behavior required to achieve socially
interesting state in agent societies is also described.
- 7.3
-
We choose to evaluate different aspects of negotiation processes in a large number of simulations. The efficiency of the negotiation settings is quantified by means of a comparison with optimal solutions estimated by centralized techniques.
We also evaluate the impact of
the transaction cardinality, of the graph connectivity and the quality
of provided solutions. We show that the use of large bilateral
transactions is not essential to achieve optimal allocations. Indeed,
it does not lead to significant improvements of the solution but to an
important increase of the computational costs. Bilateral transactions
of restricted cardinality are sufficient to achieve socially
interesting allocations.
- 7.4
-
The most efficient negotiation policies are summarized in Table
7 according to the social welfare notion considered.
- Utilitarian societies:
- A negotiation policy based on social gifts is sufficient to achieve optimal allocations when complete contact graphs are considered. This negotiation policy also leads to the best results on restricted graphs (structured and random graphs).
- Egalitarian societies:
- The use of bilateral transactions cannot guarantee the achievement of optimal allocations, even on complete contact graphs. However, a negotiation policy based on social gifts and social swaps is sufficient to achieve socially efficient allocations.
Table 7:Summary of efficient negotiation policies according to different scenarios Contact graph
ClassWelfare notions Utilitarian Egalitarian Complete optimal
social 〈1, 0〉 transactionssuboptimal (99%)
social 〈1, 0〉 transactionsRestricted suboptimal
social ''up to 〈1, 1〉'' transactionssuboptimal
social ''up to 〈1, 1〉'' transactions
- 7.5
-
Unsurprisingly, we find that the topology of the contact graphs has a significant impact on the efficiency of the negotiation processes, yet lessened when utilitarian societies are considered.
A very weak mean connectivity will drastically affect the efficiency whereas an irregular topology will not.
In fair artificial societies, a more important connectivity is
required to achieve fair allocations. Regular topologies also lead to
better results because isolated agents trap resources easily, affecting the efficiency of the negotiations.
 References
References
-
ALBERT, R. & BARABáSI, A. (2002).
Statistical Mechanics of Complex Networks.
Reviews of Modern Physics 74(1), 47-97. [doi:10.1103/RevModPhys.74.47]
ANDERSSON, M. & SANDHOLM, T. (1998). Contract types for satisficing task allocation: II experimental results. In: AAAI Spring Symposium Series: Satisficing Models, vol. 17. USA, California, Stanford University: AAAI Press.
ARROW, K., SEN, A. & SUZUMURA, K. (2002). Handbook of social choice and welfare, vol. 1. Elsevier.
BACHRACH, Y. & ROSENSCHEIN, J. (2008). Sequential auctions for the allocation of resources with complementarities. In: Proceedings of the 7th international joint conference on autonomous agents and multiagent systems (AAMAS'2008). Honolulu, USA.
BRAMS, S. & TAYLOR, A. (1996). Fair Division: From Cake-Cutting to Dispute Resolution. Cambridge University Press. [doi:10.1017/cbo9780511598975]
CAMERER, C. (2003). Behavioral game theory. University Press Princeton.
CHEVALEYRE, Y., ENDRISS, U. & MAUDET, N. (2007). Allocating goods on a graph to eliminate envy. In: Proceedings of the 22nd National conference on artificial intelligence (AAAI'2007), vol. 22(1). MIT and AAAI.
CHEVALEYRE, Y., ENDRISS, U. & MAUDET, N. (2010). Simple negotiation schemes for agents with simple preferences: Sufficiency, necessity and maximality. Autonomous Agents and Multi-Agent Systems 20(2), 234-259. [doi:10.1007/s10458-009-9088-7]
DE WEERDT, M., ZHANG, Y. & KLOS, T. (2007). Distributed task allocation in social networks. In: Proceedings of the 6th international joint conference on Autonomous agents and multiagent systems (AAMAS'2007). ACM. [doi:10.1145/1329125.1329217]
DEKKER, A. (2007). Studying organisational topology with simple computational models. Journal of Artificial Societies and Social Simulation 10(4), 6. https://www.jasss.org/10/4/6.html.
DOYLE, J. (2004). Prospects for preferences. Computational Intelligence 20(2), 111-136. [doi:10.1111/j.0824-7935.2004.00233.x]
DUNNE, P. & CHEVALEYRE, Y. (2008). The complexity of deciding reachability properties of distributed negotiation schemes. Theoretical Computer Science 396, 113-144. [doi:10.1016/j.tcs.2008.01.031]
DUNNE, P., WOOLDRIDGE, M. & LAURENCE, M. (2005). The complexity of contract negotiation. Artificial Intelligence 164(1-2), 23-46. [doi:10.1016/j.artint.2005.01.006]
ENDRISS, U. & MAUDET, N. (2005). On the Communication Complexity of Multilateral Trading: Extended Report. Autonomous Agents and Multi-Agent Systems 11, 01-107. [doi:10.1007/s10458-005-1080-2]
ENDRISS, U., MAUDET, N., SADRI, F. & TONI, F. (2006). Negotiating Socially Optimal Allocations of Resources. Journal of Artificial Intelligence Research 25, 315-348.
ERDŐS, P. & RéNYI, A. (1959). On Random Graphs. Publicationes Mathematicae 6, 290-297.
ESTIVIE, E., CHEVALEYRE, Y., ENDRISS, U. & MAUDET, N. (2006). How Equitable is Rational Negotiation? In: AAMAS'06 - Autonomous Agents and Multiagent Systems. Japan, Hakodate: ACM Press. [doi:10.1145/1160633.1160788]
GALSTYAN, A., CZAJKOWSKI, K. & LERMAN, K. (2005). Resource Allocation in the Grid with Learning Agents. Journal of Grid Computing 3(1), 91-100. [doi:10.1007/s10723-005-9003-7]
GIOVANNUCCI, A., RODRIGUEZ-AGUILAR, J. A., REYES, A., NORIA, F. X. & CERQUIDES, J. (2004). Towards automated procurement via agent-aware negotiation support. In: AAMAS '04: Proceedings of the Third International Joint Conference on Autonomous Agents and Multiagent Systems. Washington, DC, USA: IEEE Computer Society.
LIEBERMAN, E., HAUERT, C. & NOWAK, M. (2005). Evolutionary dynamics on graphs. Nature 433(7023), 312-316. [doi:10.1038/nature03204]
MAS-COLELL, A., WHINSTON, M. & GREEN, J. (1995). Microeconomic Theory. Oxford University Press.
MONTET, C. & SERRA, D. (2003). Game theory and economics. Palgrave Macmillan.
MOULIN, H. (1988). Axioms of cooperative decision making. Cambridge University. [doi:10.1017/ccol0521360552]
NONGAILLARD, A., MATHIEU, P. & EVERAERE, P. (2010). Nash welfare allocation problems : Concrete issues. In: In proceedings of the IEEE/WIC/ACM International Conference on Intelligent Agent Technology (IATÄô2010).
NONGAILLARD, A., MATHIEU, P. & JAUMARD, B. (2008). A multi-agent resource negotiation for the utilitarian social welfare. In: Proceedings of the 9th International Workshop Engineering Societies in the Agents World (ESAW'2008), vol. 5485 of Lecture Notes on Artificial Intelligence. Springer.
NONGAILLARD, A., MATHIEU, P. & JAUMARD, B. (2009). A realistic approach to solve the nash welfare. In: Proceedings of the 7th International conference on Practical Applications of Agents and Multi-Agents Systems (PAAMS'2009), vol. 55 of Practical Advances in Intelligent and soft computing. Springer. [doi:10.1007/978-3-642-00487-2_40]
RAMEZANI, S. & ENDRISS, U. (2009). Nash social welfare in multiagent resource allocation. In: Proceedings of the 11th International Workshop on Agent-Mediated Electronic Commerce (AMEC-2009). Springer.
SANDHOLM, T. (1998). Contract Types for Satisficing Task Allocation: I Theoretical Results. In: AAAI Spring Symposium: Satisficing Models, vol. 99. USA, California, Stanford University: AAAI Press.
SANDHOLM, T. (2002). Algorithm for optimal winner determination in combinatorial auctions. Artificial Intelligence 135(1-2), 1-54. [doi:10.1016/S0004-3702(01)00159-X]
XIANYU, B. (2010). Social preference, incomplete information, and the evolution of ultimatum game in the small world networks: An agent-based approach. Journal of Artificial Societies and Social Simulation 13(2), 7. https://www.jasss.org/13/2/7.html.
ZOETHOUT, K., JAGER, W. & MOLLEMAN, E. (2010). When does a newcomer contribute to a better performance? a multi-agent study on self-organising processes of task allocation. Journal of Artificial Societies and Social Simulation 13(3), 7. https://www.jasss.org/13/3/7.html.