Introduction
Authors and reviewers are central actors in the peer review process. Several simulation studies have focused on their respective roles to explore how they could influence the peer review process in science funding and journal publication. Results indicate many ways in which author and reviewer cognitive features or behavioural patterns can be detrimental to (or beneficial for) the performance of peer review systems. For instance, some studies have explored what happens if all (or some) reviewers decide not to commit to their task and return inaccurate reviews (e.g., Righi & Takács 2017; Roebber & Schultz 2011; Thurner & Hanel 2011; Wang et al. 2016). Other studies have explored the consequences of deliberate reviewer strategies, such as reviewers systematically overrating or underrating submissions in order to outcompete the authors (Cabotà, Grimaldo, & Squazzoni 2013; Sobkowicz 2015 , 2017) or as a response to their own past experiences as authors (Bianchi & Squazzoni 2015; Squazzoni & Gandelli 2013a). Some of these studies also explored the consequences of author strategies such as minimizing the effort and resources invested in the preparation of their submission (Squazzoni & Gandelli 2013a) or, similarly, prioritizing the quantity of submissions over their quality (Roebber & Schultz 2011).
Crucially, many of these studies are directly based on, or have been heavily influenced by, a few so-called ‘root models’, with whom they share fundamental assumptions (Feliciani et al. 2019). Some of these assumptions relate to the evaluation scale. For example, while most of these models[1] define the evaluation scale as a real number within a finite range, the actual evaluation scale in peer review processes is typically a coarse-grained Likert scale with few categories (e.g. a progressive range from “Very poor”/”Reject” to “Outstanding”/”Accept”). Secondly, all these models implicitly assume that all peer reviewers interpret the scale in the exact same way. However, in reality reviewers may differ in defining and assessing what exactly qualifies, for example, as an “outstanding” submission (Wardekker et al. 2008).
Some research has tried to relax these assumptions. For instance, Paolucci & Grimaldo (2014) ran a simulation study comparing an evaluation scale with 10 categories with one with a binary one. In the former, reviewers return their evaluation in the form of an integer between 1 and 10; with a binary scale, reviewers can only recommend a paper for acceptance or rejection. More recently, Morreau & Lyon have also proposed a formal and computational model where the evaluation scale is discrete; in addition, reviewers may differ in how they interpret the categories of the evaluation scale (Lyon & Morreau 2018; Morreau & Lyon 2016).
Morreau & Lyon have introduced the concept of grade language in simulation models of peer review. A grade language is defined as a set of symbols (i.e., the grades of an evaluation scale) and their interpretations (i.e., how good a submission has to be to deserve a certain grade by a peer reviewer). Thus, a grade language can vary in terms of its heterogeneity, depending on how differently these grades are interpreted across reviewers. For example, the presence of reviewers with very different grading standards signals a highly heterogeneous grade language.
Empirical research suggests that reviewers may differ in how they understand evaluation grades, lending more importance to understanding grade language heterogeneity (Morgan 2014; Wardekker et al. 2008). Furthermore, simulation research has shown that, counterintuitively, heterogeneity is not necessarily detrimental to the quality of a collective judgement (Lyon & Morreau 2018). A collective judgment made by a group of reviewers with different grading standards can, under some circumstances, be more accurate than the collective judgement by a homogeneous group. These findings can have practical consequences for editorial policies. To give one example, if the editor of an academic journal wishes to standardise reviewer evaluations (e.g., by training reviewers thereby homogenizing reviewers’ grading language), the editor would be better informed if they could know in which ways and under which circumstances standardised reviewers are more desirable than reviewers with heterogeneous grading standards.
In this paper, we study the effects of grade language heterogeneity in an agent-based model (ABM) of peer-review from the literature. It is important to note that discrete scales and grade language heterogeneity are two related assumptions. Since the set of symbols in a grade language is finite, modelling grade languages implies a discrete evaluation scale. That is, one cannot be studied without making assumptions about the other. For this reason, we study grade language heterogeneity by implementing both grade languages and discrete evaluation scales into an existing model. The model we revisit is the well-known model of journal peer review by Squazzoni & Gandelli (2012a, 2012b, 2013a), hereafter: ‘SG’.
The SG model examines the peer review process in academic publishing vis-à-vis author and reviewer behavioural strategies. The reasons we chose this model are its relevance and simplicity: in fact, this model emerged as influential in the literature of simulation models of peer review, and served as a basis for (or inspired) several follow-up simulation studies on reviewer and author strategies (Feliciani et al. 2019). Showing that grade language heterogeneity affects the dynamics of the SG model would demonstrate the point that work building on the SG model should not overlook this assumption. This also applies to the more general modelling literature on peer review. Thus, by adding both discrete evaluation scales and grade language heterogeneity to the SG model, our approach tackles the following research question: how do results change in peer review modelling when introducing more realistic assumptions about reviewer behaviour (i.e., discrete evaluation scales and grade language heterogeneity)?
In the following sections, we outline the rationale behind (plus functioning of) the SG model and introduce the concept of grade languages (Section 2). We then outline our simulation experiment (Section 3); results and discussion follow.
Background
The premise of the work by SG is that reviewers are “unreliable”, meaning they incorrectly evaluate author submissions (Bornmann 2011; Cicchetti 1991). Even if reviewers were completely reliable, peer review would still not necessarily promote good quality submissions and filter out poor ones (Stinchcombe & Ofshe 1969). This led SG to inquire what incentivises scholars to be gatekeepers of good quality science (Squazzoni & Gandelli 2013a; Squazzoni & Takács 2011). In turn, the SG model focuses on how author and reviewer behaviour can impact different aspects (such as efficacy, efficiency, and inequality) of the peer review process for an academic journal publication.
In SG, the process of peer review is simplified to some essential components. One important simplifying assumption is that submissions have an objective level of quality (hereafter: ‘true quality’), a real number ranging between the theoretical minimum and maximum quality levels. Furthermore, only authors and reviewers are considered as agents involved in the peer review process (thus ignoring other roles, such as editors). Further, SG assumes that each manuscript is reviewed by only one reviewer. Lastly, this journal publication peer review only consists of one round of review, where authors submit manuscripts for publications, reviewers evaluate the submission, and the best-rated manuscripts are published.
At the core of the SG model (and other follow-up work, e.g. Bianchi & Squazzoni 2015; Cabotà, Grimaldo, & Squazzoni 2013) lies the idea that scholars constantly face a trade-off when they have a finite amount of resources (e.g., time) that they must allocate to two competing tasks: to work on their own manuscript or to review someone else’s. How resources are invested in each task is dependent on motives of the reviewers and authors: as we will illustrate, scholars’ sense of fairness and reciprocating attitude influences the resources that they invest in authoring and reviewing.
Overview of the SG model
Since our study implements SG as it was originally defined and coded in those earliest publications of simulation of peer review systems/processes, we will henceforth refer to Squazzoni & Gandelli (2012a, 2013a) for the formal definition of the model. A discussion of our implementation of SG, along with pointers to the original code (Squazzoni & Gandelli 2013b), our scripts and documentation, is included in Appendix I. Here we provide an overview of the original model scheduling and relevant entities, attributes and processes.
Scholars are the main entities in the system, and their most important attribute is the amount of resources they have (assumed to be zero at the start of the simulation). Resources are spent in authoring and reviewing submissions and are gained at a fixed rate as time progresses. Scholars can further increase their resources by getting their own submissions published.
At every time step of the simulation, each agent either plays the role of a reviewer or of an author; the role is drawn with a uniform probability. Once roles are assigned, each author produces a submission of a given quality and a randomly chosen reviewer evaluates the submission with some degree of accuracy[2].
The quality of the submissions and the accuracy of the reviews are key in SG. “Quality” is assumed to be the intrinsic, unobservable true worth of a submission. Thus, a submission of high quality is a submission that highly deserves publication. Furthermore, accuracy is a property of reviewers, which determines the magnitude of the error the reviewer can make when reviewing (i.e. when estimating a submission’s quality). In the SG model, quality and accuracy are endogenously determined. So authors should produce high quality submissions in order to maximise their chance of being published. To increase the submission quality, authors must invest more of their resources in authoring. In similar fashion, the amount of resources available to reviewers determines both the accuracy and the costs of their review, so that more resources invested in review result in higher quality reviews.
Each simulation step ends with the determination of which submissions get published. Submissions are ranked based on the review they received. The ones ranking higher than the baseline are published, and their authors rewarded with extra resources. The baseline is determined by the acceptance rate of the journal (i.e., the proportion of proposals that are to be published at each time step).
Reviewer and author strategies in SG
In SG, scholars have one behavioural choice: to be reliable, or unreliable. Reliable authors invest their resources fully to produce and submit a good quality submission; likewise, reliable reviewers make the largest resource investment in order to make accurate reviews. By contrast, unreliable behaviour consists of low resource investments and poor-quality submissions (by authors) and inaccurate reviews (by reviewers). A set of rules, named ‘scenario’, determines how scholars will behave. We build on the scenarios introduced in SG:
- No reciprocity. In this scenario, reviewer behaviour is based on chance: with a probability of 0.5 reviewers behave reliably (thus, making a high investment of resources and returning an accurate review); with a complementary probability, they behave unreliably. Author behaviour, by contrast, is assumed to be always reliable (i.e., a constant combination of high investment and high-quality submissions).
- Indirect reciprocity. Reviewers only behave reliably if their own most recent submission was accepted for publication. Authors are assumed to be always reliable.
- Fairness. Reviewers calculate how fairly their own most recent submission was evaluated. If their previous submission was given a grade close to what they believe was its true quality (regardless of whether it was eventually published), they behave reliably. Authors are assumed to be always reliable.
- Self-interested authors. Reviewers behave similarly as in the indirect reciprocity scenario (i.e. reliable only if their most recent submission was published). Authors are assumed to be reliable only if their previous submission was published (and unreliable otherwise).
- Fair authors. Reviewers behave similarly as in the fairness scenario (i.e., reliably is assumed only if their most recent submission was evaluated fairly). Likewise, authors are assumed reliable only if their previous submission was evaluated fairly.
These scenarios revolve around fairness and reciprocity as guides for scholars’ reliability and are a subset of the possible combinations of random, consistent, fairness-inspired and reciprocating behaviour of authors and reviewers. These scenarios are studied across different levels of acceptance rate (namely 0.25, 0.5, 0.75). Acceptance rate is an important input parameter defining the percentage of author's submission accepted for publication, thus representing high- or low-competitive environments in the model.
Extending the SG model
The SG model, along with a series of follow-ups (e.g., Bianchi & Squazzoni 2015; Cabotà et al. 2014; Righi & Takács 2017), implicitly makes some assumptions about the grade language. For instance, SG assumes that the evaluation scale is continuous: reviewers, for example, return their evaluation in the form of a real number between 0 and 1. Second, SG assume that the grades of the evaluation scale mean the same thing to all scholars (i.e., the grade language is perfectly homogeneous).
However, these assumptions do not necessarily mirror actual peer review processes. Reviewers may not give grades as precise as a continuous scale would require. Real peer review processes typically ask reviewers to return evaluations on a discrete scale (e.g., a Likert scale, with categories ranging from “very bad” to “very good” or other similar labels). There is then an issue of semantic diversity among reviewers. Research has highlighted that different individuals often have different understandings of what those grades mean (Morgan 2014; Wardekker et al. 2008). In other words, the grade language of a real peer review system is more likely to have some heterogeneity instead of being fully homogenous.
Recent simulation experiments on the wisdom of crowds (Lyon & Morreau 2018; Morreau & Lyon 2016) show that grade language heterogeneity has counterintuitive consequences for the performance of a panel of experts. Assume a panel is tasked with the estimation of something measurable, like the quality of a submission. The authors show that the aggregation of the scores by the panel members can be closer to the true quality if panel members have different interpretations of the evaluation scale. This result has important implications for peer review, where one often does not know if there is consistency between reviewers (i.e., good inter-scorer reliability) or if such consistency indicates good quality review at all. In sum, the impact of low inter-scorer reliability is an open problem (Bornmann 2011; Lee et al. 2013).
To our knowledge, grade language heterogeneity has never been implemented in ABMs of peer review. Therefore, we do not know how grade language heterogeneity affects peer review in repeated interactions between interdependent scholars. To explore these effects, we reimplemented and extended the SG model by adding grade languages (and thus also discrete evaluation scales) to assess whether, and how, grade language heterogeneity interacts with author and reviewer strategies — ultimately affecting peer review outcomes.
Implementation of discrete scales and grade language heterogeneity
As we noted above, in SG the evaluation scale is continuous and the grade language is homogeneous. To test how the granularity of the evaluation scale and grade language heterogeneity affect the SG model, we start by discretizing the evaluation scale. We then compare three levels of discretization: with 5, 10, and 20 categories. With 5 categories we mimic a typical Likert-style evaluation scale in peer review. And by increasing the number of categories, we increase the granularity of the scale, where more categories approach a situation where the evaluation scale is continuous.
Specifically, the discretization is done by means of a list of thresholds in the range of the evaluation scale, [0,1]. An evaluation scale with 5 categories requires 4 thresholds. For example, the discretization thresholds {0.2, 0.4, 0.6, 0.8} partition the continuous evaluation scale [0,1] into five regular intervals. Suppose a submission is judged to be worth 0,394 on the continuous scale [0,1]. This submission will fall in the second interval set by the thresholds, that is between 0,2 and 0.4: thus, the continuous value 0.394 in [0,1] is discretised into the score 2 on the discrete scale from 1 to 5. Similarly, a scale with 10 categories will require 9 thresholds {0.1, 0.2, 0.3, etc.}, and 20 categories will require 19 thresholds {0.05, 0.1, 0.15, …}.
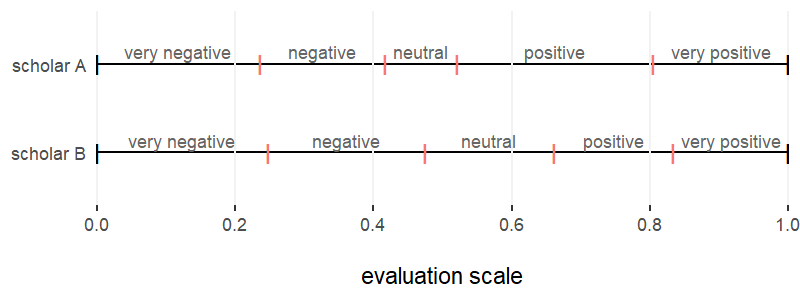
We denote a ‘homogenous grade language’ as a situation where the thresholds are spaced evenly, like in the example above, and all reviewers adopt the same thresholds to discretise their evaluation. When the grade language is homogeneous, we can state that all reviewers have the same interpretation of the grades. By contrast, with heterogeneous grade language, reviewers may have different interpretations of the grades. Grade language heterogeneity is therefore modelled by giving each scholar a different set of thresholds. Figure 1 exemplifies this by visualizing the discretization thresholds of two scholars under grade language heterogeneity. For clarity, the discrete scores 1 through 5 are labelled “very negative” to “very positive”: the figure shows how scholars map these labels differently on the underlying continuous evaluation scale via adopting different sets of thresholds (marked in orange).
We generate a heterogeneous grade language by drawing, for each reviewer, a set of thresholds from a uniform distribution in the range [0,1], and then by ordering the sets from its smallest value (first) to the biggest (last) threshold. The violin plots in Figure 2 show the resulting distribution of thresholds of a 5-categories scale over the continuous evaluation.
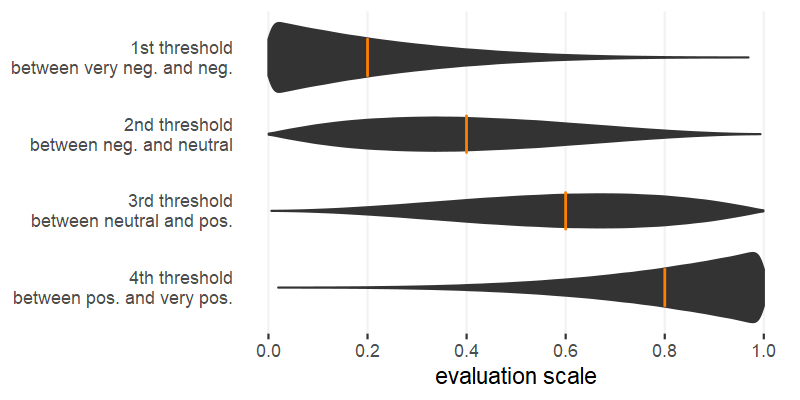
As Figure 2 shows, the procedure of ordering a set of thresholds drawn from a uniform distribution has two characteristics. First, the thresholds are noisy. For example, the first threshold tends to assume low values (0.2 on average), but occasionally takes values > 0.5. A reviewer with such a high first threshold is a markedly severe reviewer, who would rate 1/5 (i.e., “very negative”) all proposals with a quality lower than such a high threshold. The second characteristic concerns the average of each threshold distribution. The average is equal to the corresponding threshold in a regular partition of the continuous scale. To clarify: the thresholds to discretise the continuous evaluation scale into five regular intervals are {0.2, 0.4, 0.6, 0.8}. Figure 2 shows that the first threshold distribution has, in fact, mean 0.2; the second, 0.4; and so forth. This distribution makes for a fair comparison between homogenous grade language (where the partition is regular for all scholars) and heterogeneous (where the thresholds are distributed around the same average value).
Implementing discrete scales and heterogeneous grade languages in SG is straightforward: we discretise the evaluation score using the threshold derived from a regular partition of the continuous scale (homogeneous grade language), or using scholars’ own discretization thresholds (heterogeneous grade language). More precisely, we discretise the scores in two ways. In the first case, whenever a reviewer returns their evaluation of a submission, the evaluation is transformed into a grade on the discrete scale according to the reviewer’s thresholds. The second occasion only affects the scenarios’ ‘fairness’ and ‘fair authors’. In these two scenarios, scholars behave reliably only if they deem that their most recent submission as authors was evaluated fairly. Fairness is based on the difference between the scholar’s self-perception of the quality of their submission and the reviewer’s evaluation of it. Thus, in these two scenarios, not only do we discretise the reviewer’s evaluation, we also discretise the scholar’s self-perception of the quality of their own work.
Outcome measures
To measure how grade language heterogeneity can impact peer review dynamics, we look at the same outcome measures investigated in the SG model. The measures devised in SG capture three different dimensions of the peer review process: efficacy, efficiency, and inequality. Broadly speaking, efficacy of a peer review process can be defined as its tendency to have the best submissions published. Efficiency refers to the optimal use of resources by reviewers and authors. Lastly, inequality refers to the resulting unevenness in the distribution of resources among scholars.
These three dimensions are captured using the following indicators:
- Evaluation error refers to the percentage of high-quality submissions (i.e. worth being published) that were not published. A poor review process where considerable numbers of deserving submissions are not published has a higher evaluation error. This measure operationalises the concept of peer review efficacy.
- Resource loss is a measure of peer review efficiency. It is defined as the percentage of the sum of the resources spent on all publication-worthy submissions that were not eventually published. In other words, it measures the amount of quality that went to “waste” because deserving submissions were not published.
- Reviewing expenses are calculated as the ratio of resources invested by reviewers over the resources spent by authors. A range from [0,1] is transformed into a percentage.
- System productivity is the sum of the resources of all scholars in the system.
- Gini index captures the concept of peer review inequality. Measured over the distribution of resources among scholars, it indicates the degree to which resources are unevenly distributed. That is, 0 means all scholars have the same amount of resources, and 1 means a scholar has all the resources, while the others have none.
Expected effects of grade language heterogeneity on SG
Generally, we expect to find a difference between the SG model dynamics with homogeneous vs heterogeneous grade language. Our thinking is that heterogeneity makes reviewer evaluation more noisy. In turn, noisy evaluations mean less precision which should make harder the identification of the most deserving proposals. Additionally, noise in the determination of which submissions get published may also hinder the ability of the best scholars to further concentrate resources in their hands. We expect then that heterogeneity affects peer review efficacy (evaluation error), efficiency (resource loss) and inequality (Gini index). The expectations discussed above can be rephrased as hypotheses:
H1b.Grade language heterogeneity leads to higher resource loss.
H1c. Grade language heterogeneity leads to a lower Gini index.
Furthermore, we need to consider that the implementation of grade languages entails a discrete evaluation scale. The evaluation scale may have different levels of granularity, which also may affect the precision of reviewer evaluation. For example, a relatively coarse evaluation scale (e.g., with 5 categories) allows for less precision than a more fine-grained scale (e.g., with 10 or 20 categories). Since coarser scales mean higher evaluation noise, we expect that the granularity of the scales should affect peer review efficacy, efficiency and inequality in the same way as heterogeneous discretization thresholds. It is therefore important to separate the effects of random thresholds from the granularity of the scale. To achieve this, we test for the effects of grade language heterogeneity for different levels of granularity of the discrete scale.
Next, we focus on the differences between the SG-modelled scenarios (i.e. the rules determining scholars’ reliable vs unreliable behaviour). In principle, the reasoning behind H1a, b, c should apply to all scenarios in the same way. Finding support for these expectations would thus not change the most important conclusions from the original SG model on the comparisons between scenarios.
An even more interesting possibility is that our treatment affects some scenarios more than others, or otherwise affects the ranking of the scenarios under the different outcome variables. If this were the case, we would conclude that assuming or not assuming grade language heterogeneity (and a discrete evaluation scale) changes the prediction of the model about which scenarios perform better than others. It is difficult to anticipate in which ways each scenario will be affected by granularity and heterogeneity: therefore, we formulate an overarching hypothesis:
Simulation Experiment
The SG model was originally implemented in NetLogo and is available in the CoMSES repository (Squazzoni & Gandelli 2013b). Instead of building on the original NetLogo script, we re-implemented the SG model from scratch in the R language by following the description of the model as provided in the original papers (Squazzoni & Gandelli 2013a, 2012b) and inspecting the NetLogo scripts. The re-implementation constitutes an effort to inspect and ensure the internal validity of the model as originally designed and is recognised as a best practice in the simulation literature (Rouchier et al. 2008). The re-implementation of the SG model brought to light a number of discussion points on the internal validity of the model which would have otherwise likely gone unnoticed. Appendix 1 discusses in depth our re-implementation effort and the emergent discussion points.
The re-implementation allowed us to run a version of the SG model where we can specify the granularity of the evaluation scale and whether the grade language is homogeneous. Specifically, in our simulation experiment we manipulate two parameters:
- The number of categories in the evaluation scale: we compare three types of scales, with 5, 10 and 20 categories.
- Heterogeneity of the grade language. We compare a SG model version where the grade language is homogeneous with the heterogeneous version.
We ran 100 independent simulation runs using the same baseline configuration adopted in SG. We compare the outcome measures at the end of the simulation runs (t=200) between the various sets of conditions. In the next section, we present results assuming the middle value for acceptance rate (i.e., acceptance rate = 0.5). Appendix II discusses the results obtained with alternative acceptance rates.
Results
We proceed by breaking down simulation results following the order of H1a, b, c and H2.
Effect on peer review efficacy, efficiency and inequality
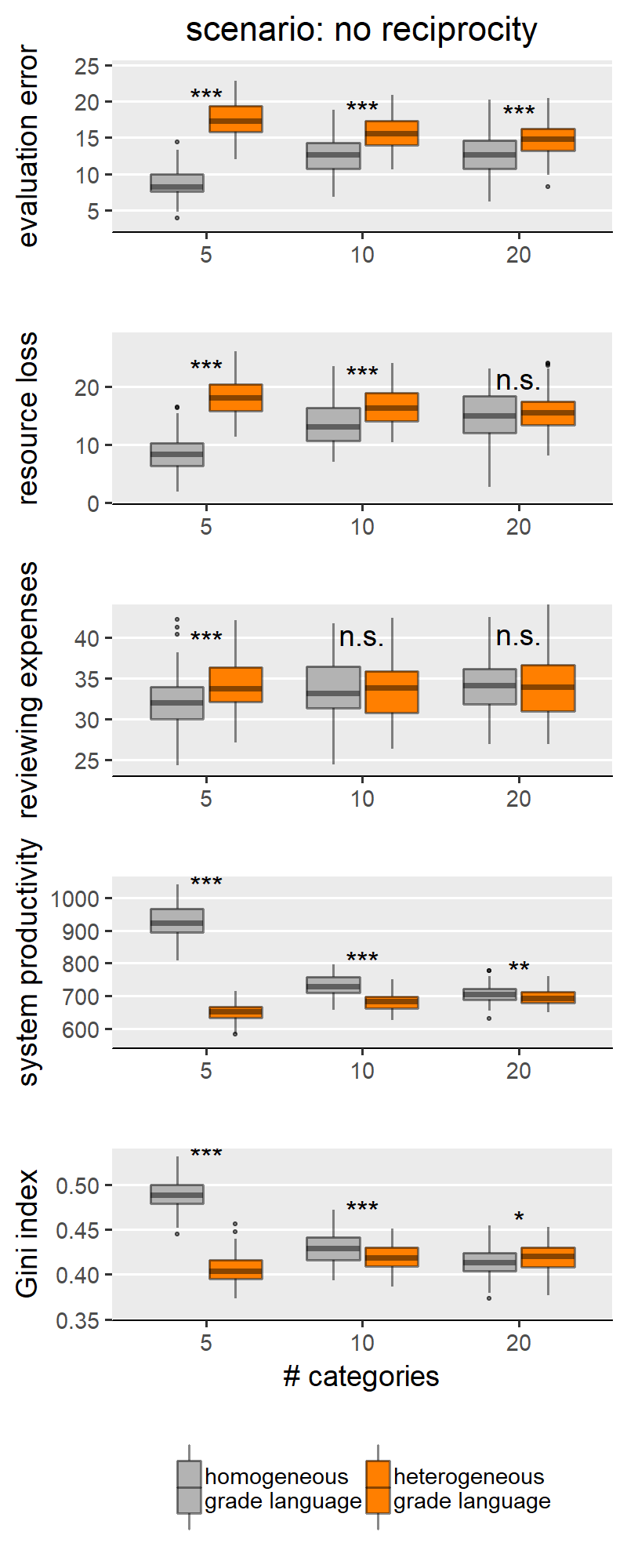
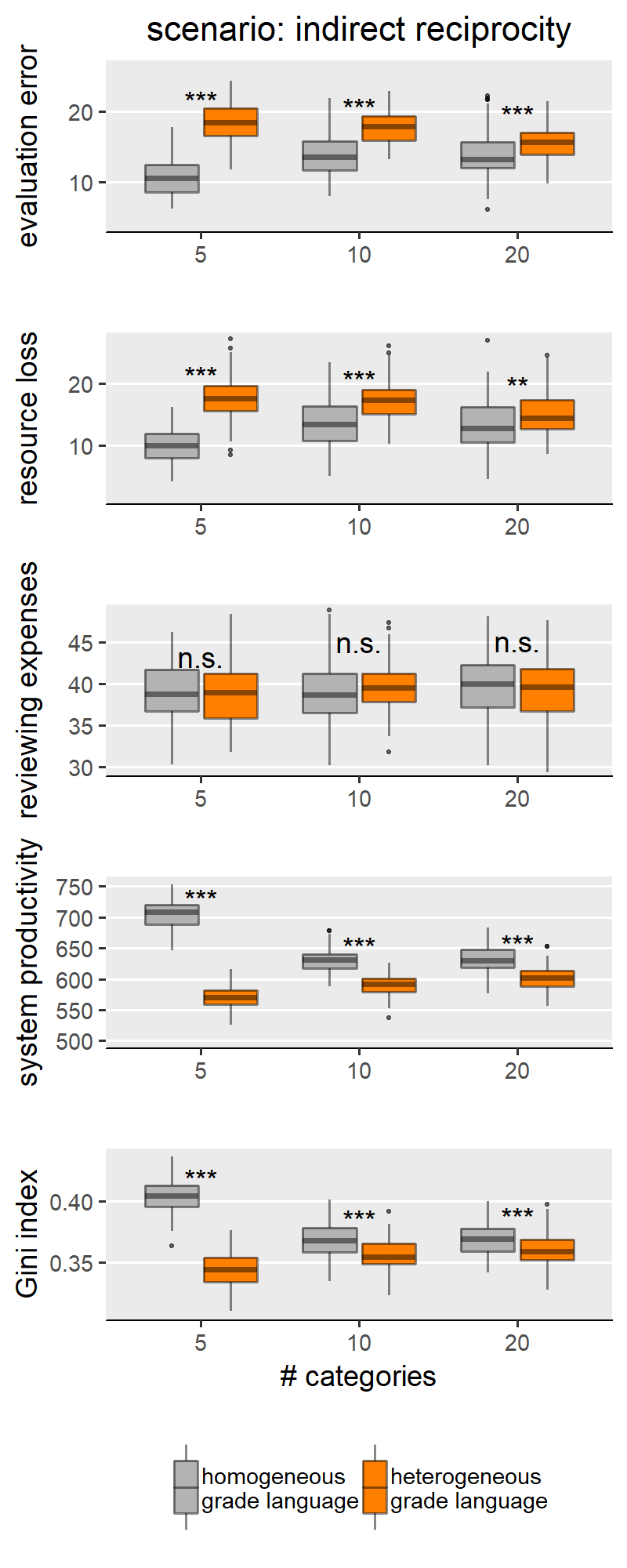
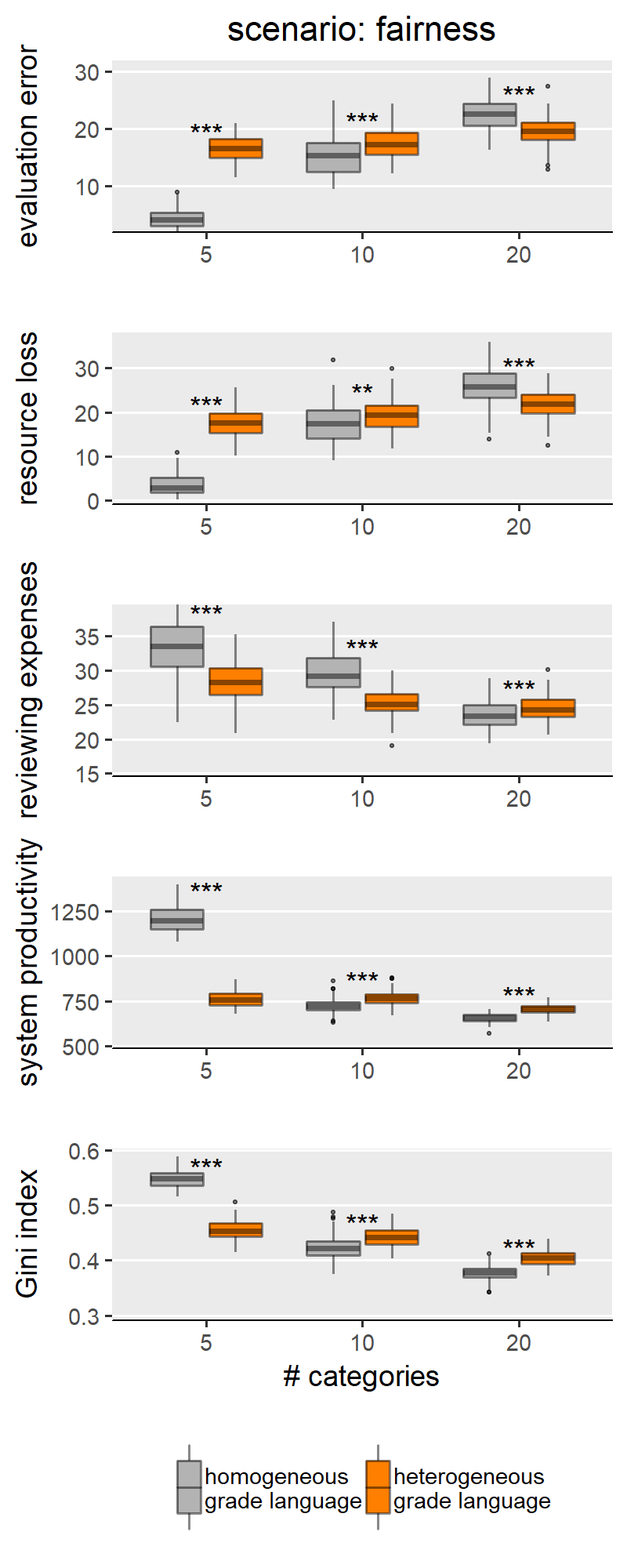
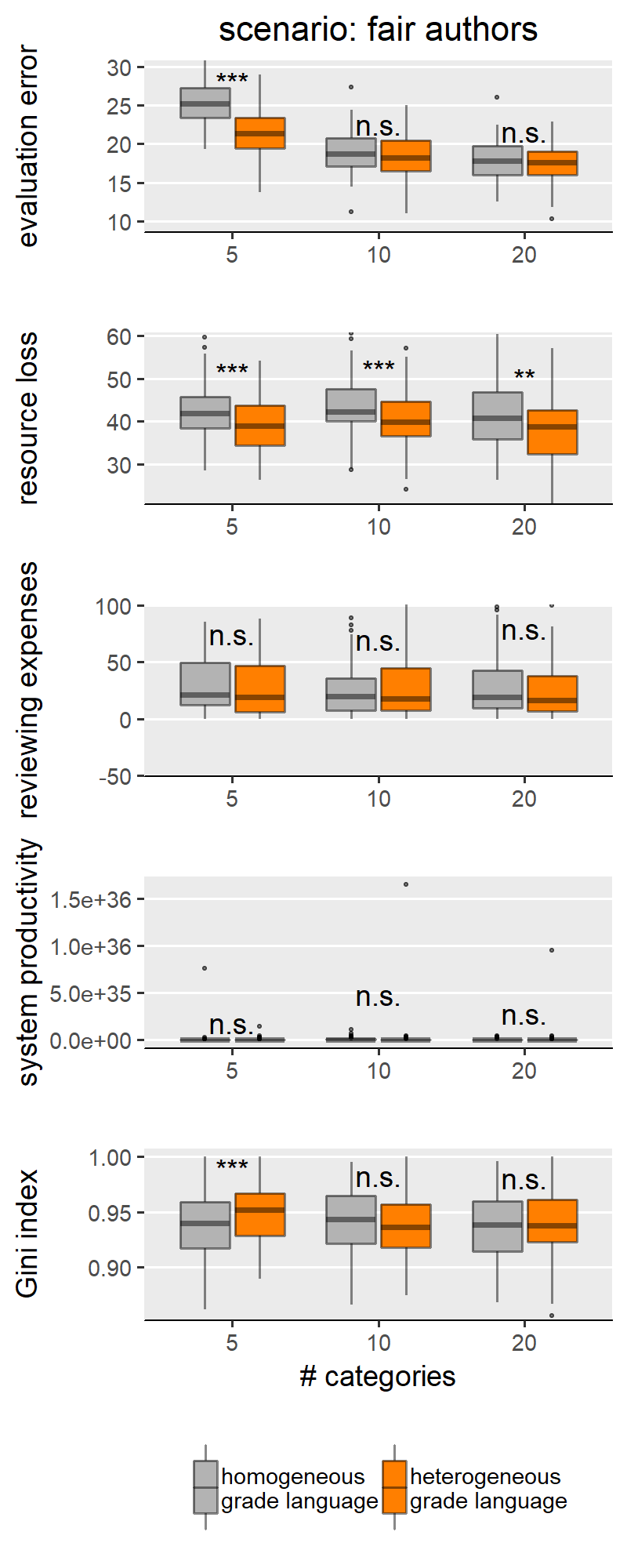
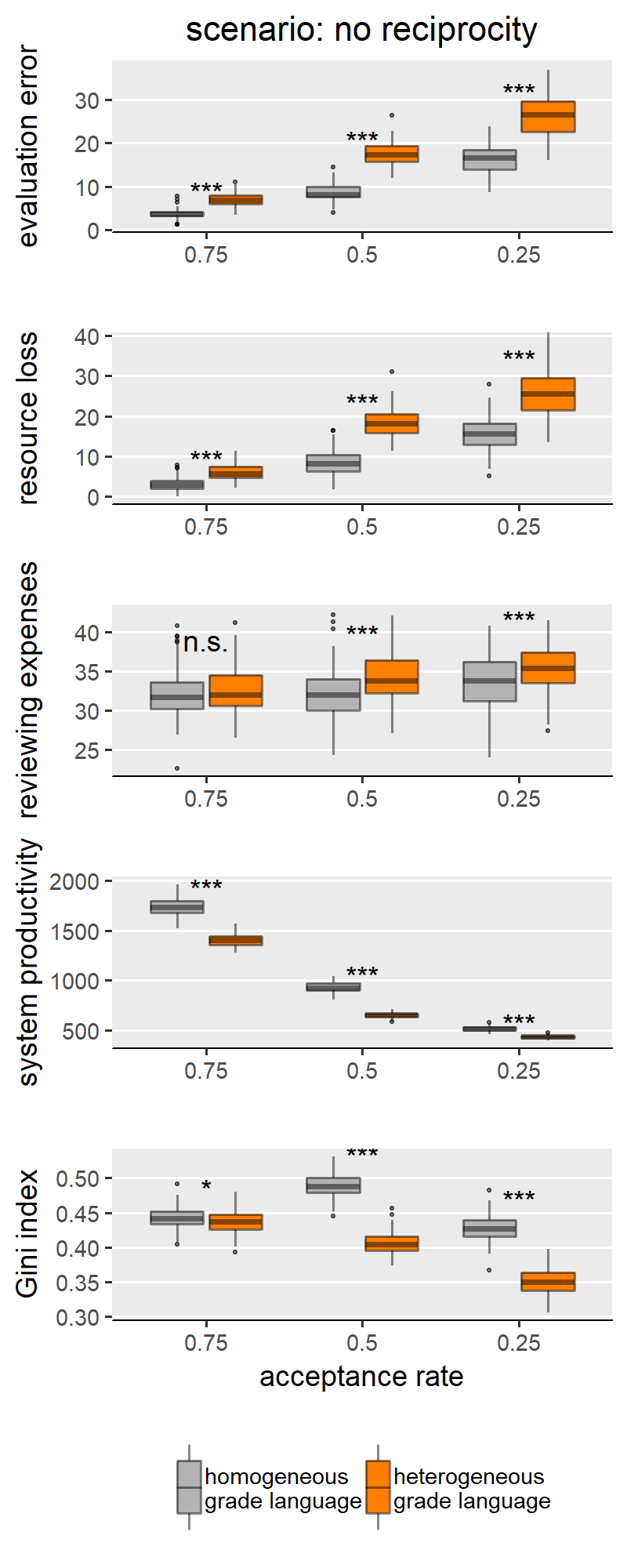
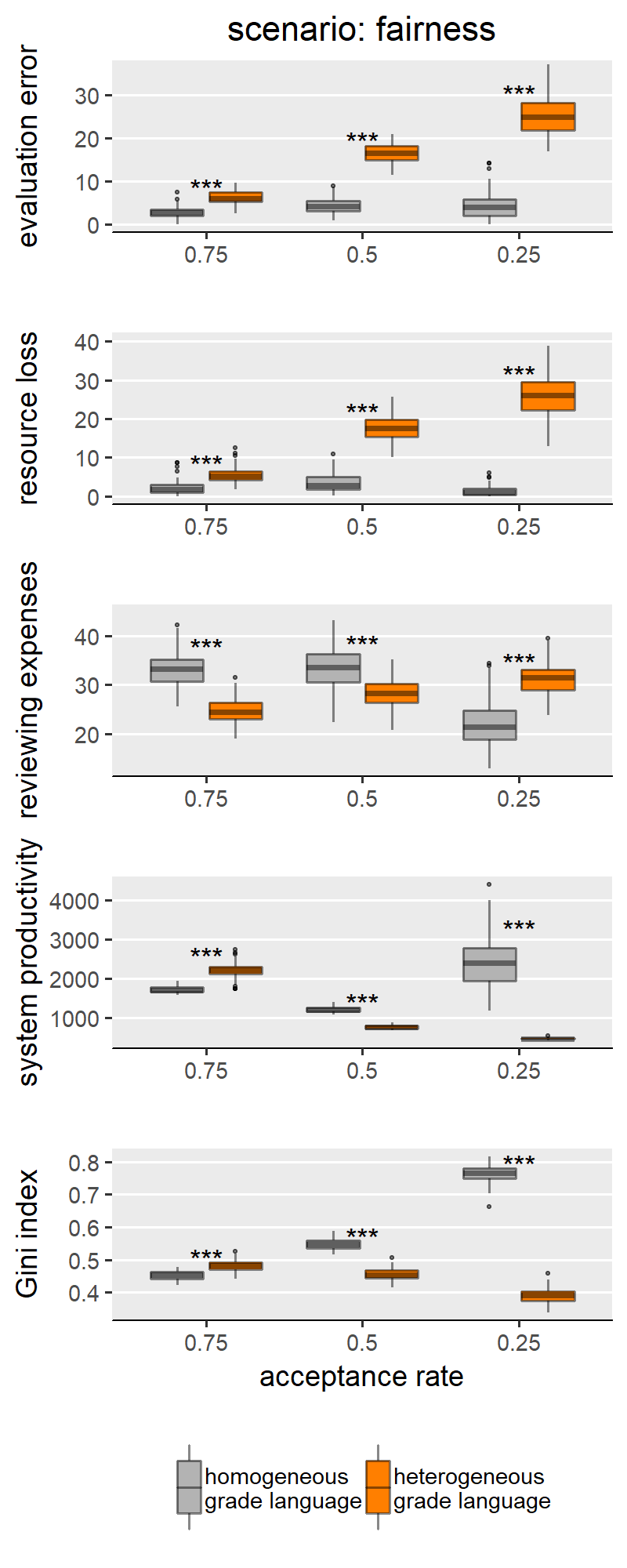
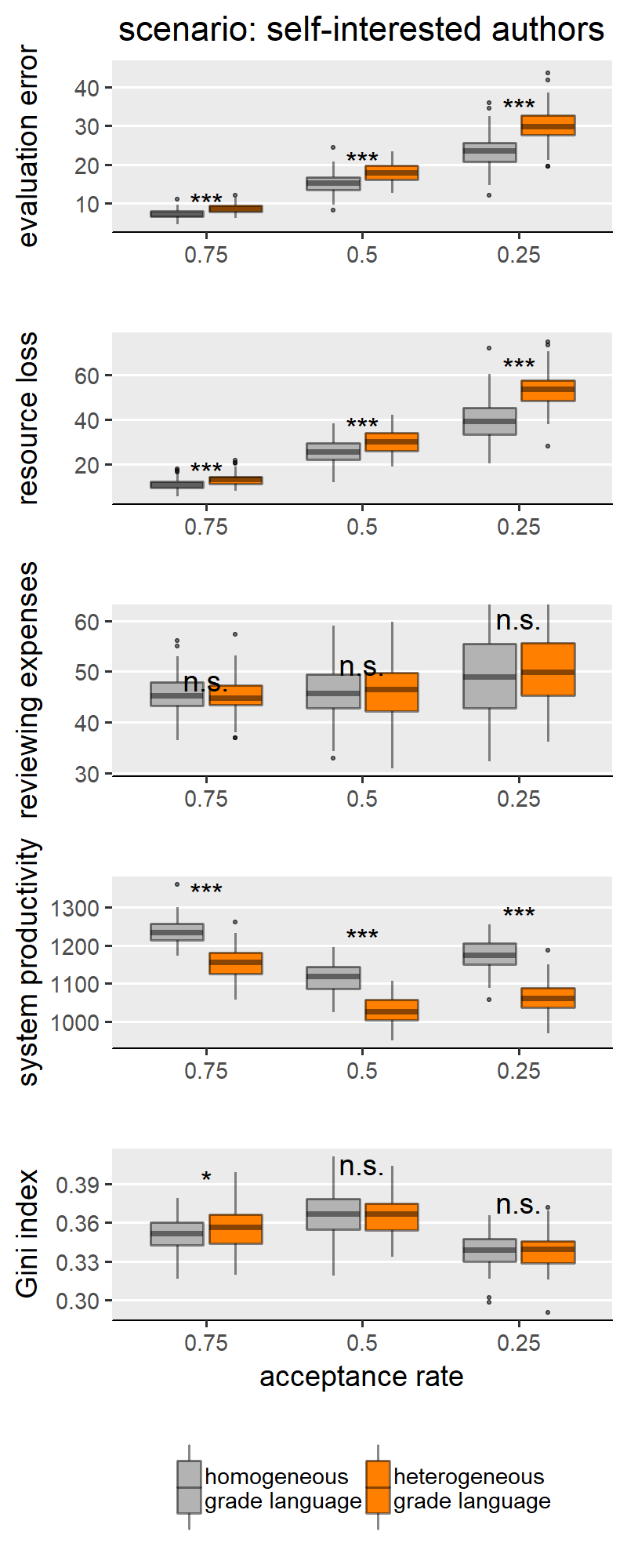
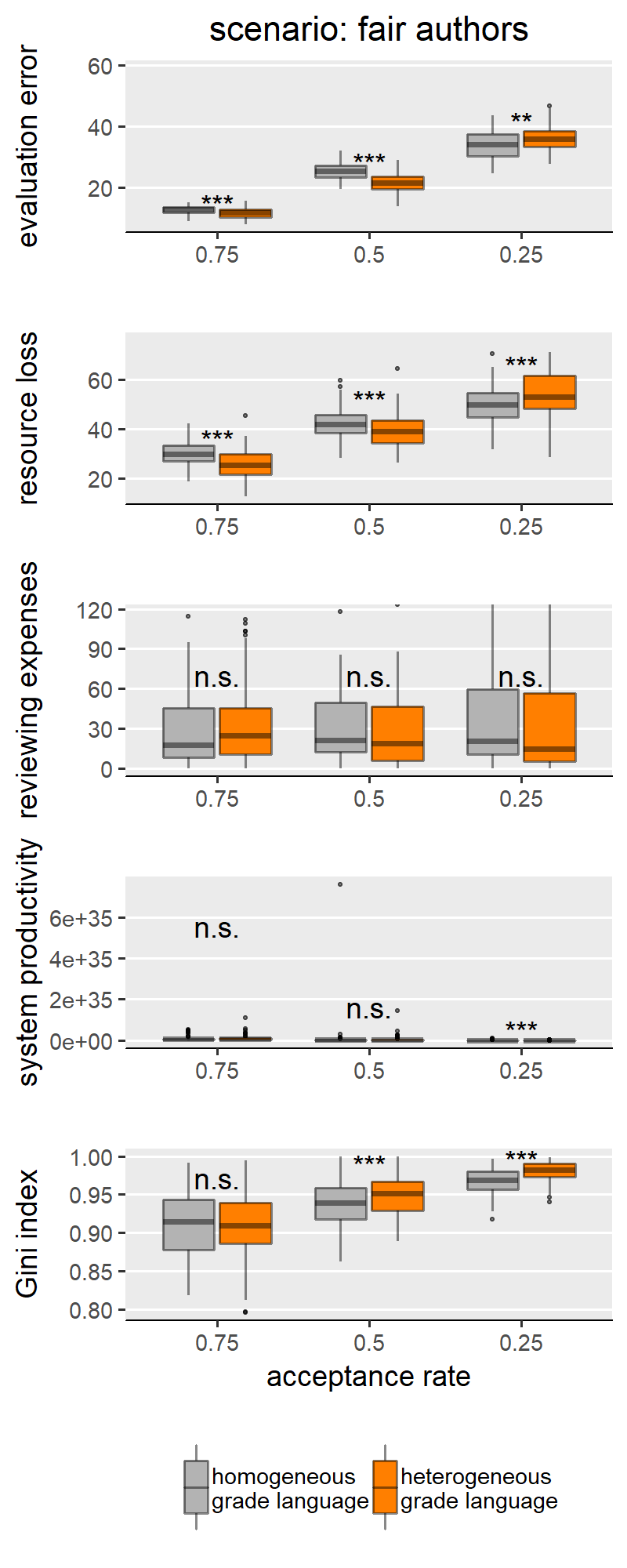
With H1a, b, c we are comparing homogeneous and heterogeneous grade languages within each SG behavioural scenario and for each of the explored levels of scale granularity. With few caveats, H1a, b, c are confirmed in only three of the five scenarios: “no reciprocity”, “indirect reciprocity” and “self-interested authors”, and not for the scenarios “fair authors” and “fairness”. Since the results from these two groups of scenarios are internally consistent, for illustration purposes the main text only shows results for the scenario “no reciprocity” as representative of the first group (Figure 3) and “fairness” for the other group (Figure 4). Plots for all scenarios are found in Appendix III.
Concerning the first group (exemplified by “no reciprocity” in (Figure 3), we indeed find that heterogeneous grade language leads to higher evaluation error (H1a), higher resource loss (1b), and lower Gini index (1c) compared to the homogeneous counterpart. We note these effects appear to be moderated by the granularity of the evaluation scale. Specifically, the effect size is larger with coarse-grained scales (i.e., with evaluation scale with 5 categories). With finer-grained scales (i.e., 10 or 20 categories), the effect grows smaller and, in a few cases, the difference between heterogeneous and homogeneous grade languages loses significance or disappears entirely. This is particularly evident in the boxplots for the Gini index in Figure 3: in this scenario, with maximal granularity (20 categories) we find that heterogeneity leads to a higher (instead of lower) Gini index. These results teach us something important: that the granularity of the scale can hamper the effect of grade language heterogeneity, and sometimes overcome it. For example, the Gini index case in the “no reciprocity” scenario.
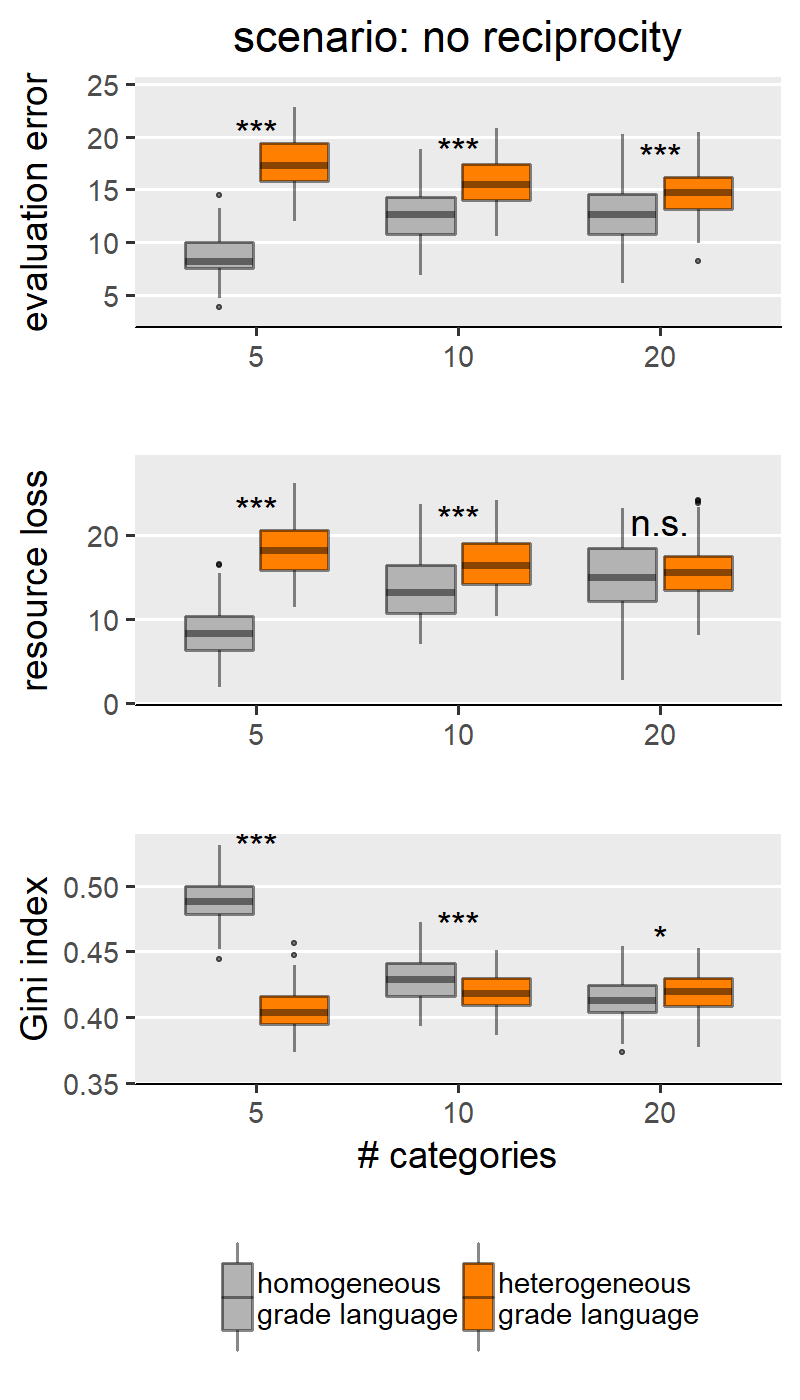
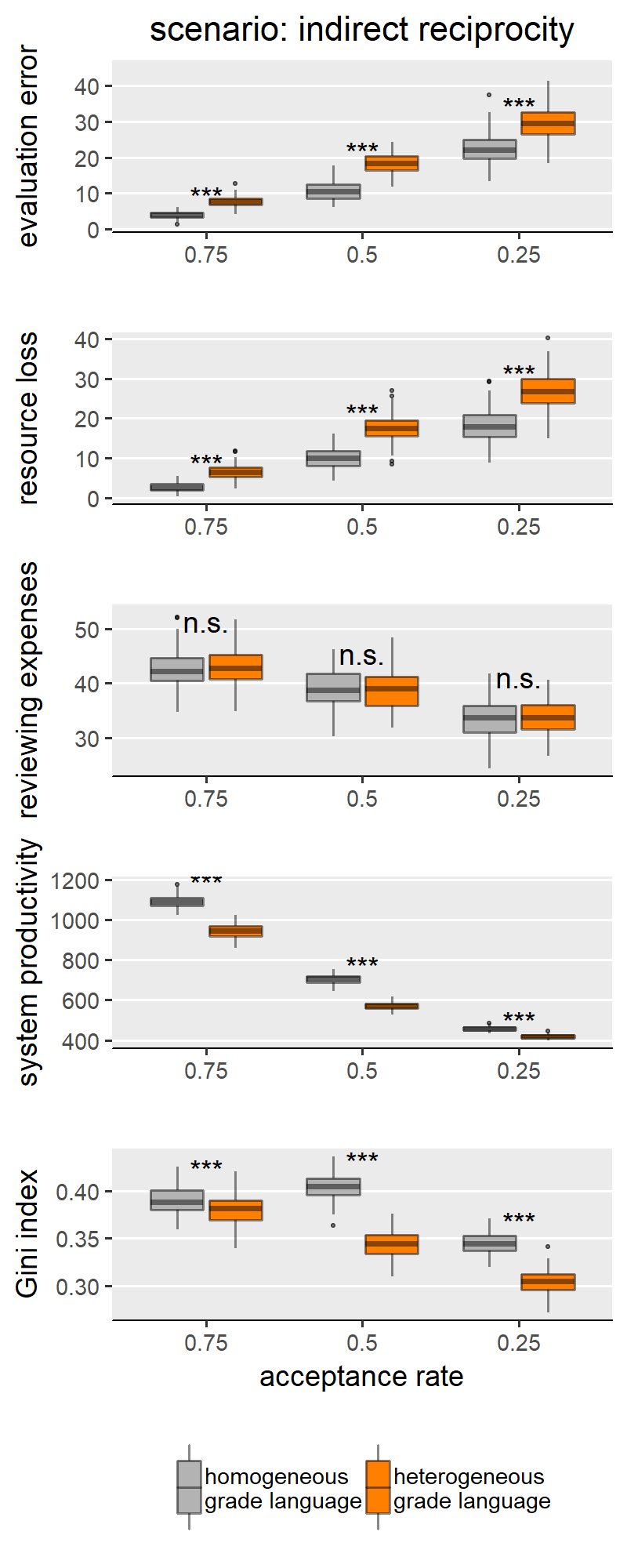
Figure 4 shows results for the scenario “fairness”, selected to represent the scenarios for which we do not find support for H1a,b,c and also includes “fair authors”. In these two scenarios, we mostly find either non-significant differences between homogeneous and heterogeneous grade languages, or effects with a sign opposite to what we hypothesised. This means that our simulations identify some conditions (i.e., combinations of scenario and scale granularity) for which a heterogeneous grade language outperforms a homogeneous one (i.e. producing less evaluation error and wasting fewer resources). We only find the effect in the predicted direction in the scenario “fairness” (Figure 4), for simulation runs with an evaluation scale with 5 categories. Thus, we believe that this, too, is to be interpreted as an effect of the granularity of the evaluation scale. The question arises why the scenarios “fairness” and “fair authors” yield results so markedly different from the first group of scenarios. Our explanation for this finding hinges on the concept of discrepancy: in these scenarios, scholars behave reliably only if their previous work was evaluated ‘fairly (i.e., in case of little discrepancy between the evaluation of their own previous work and their own self-evaluation). A discretised evaluation scale may reduce discrepancy by increasing the likelihood that scholars’ self-perceived submission quality is equal to the reviewer assessment.
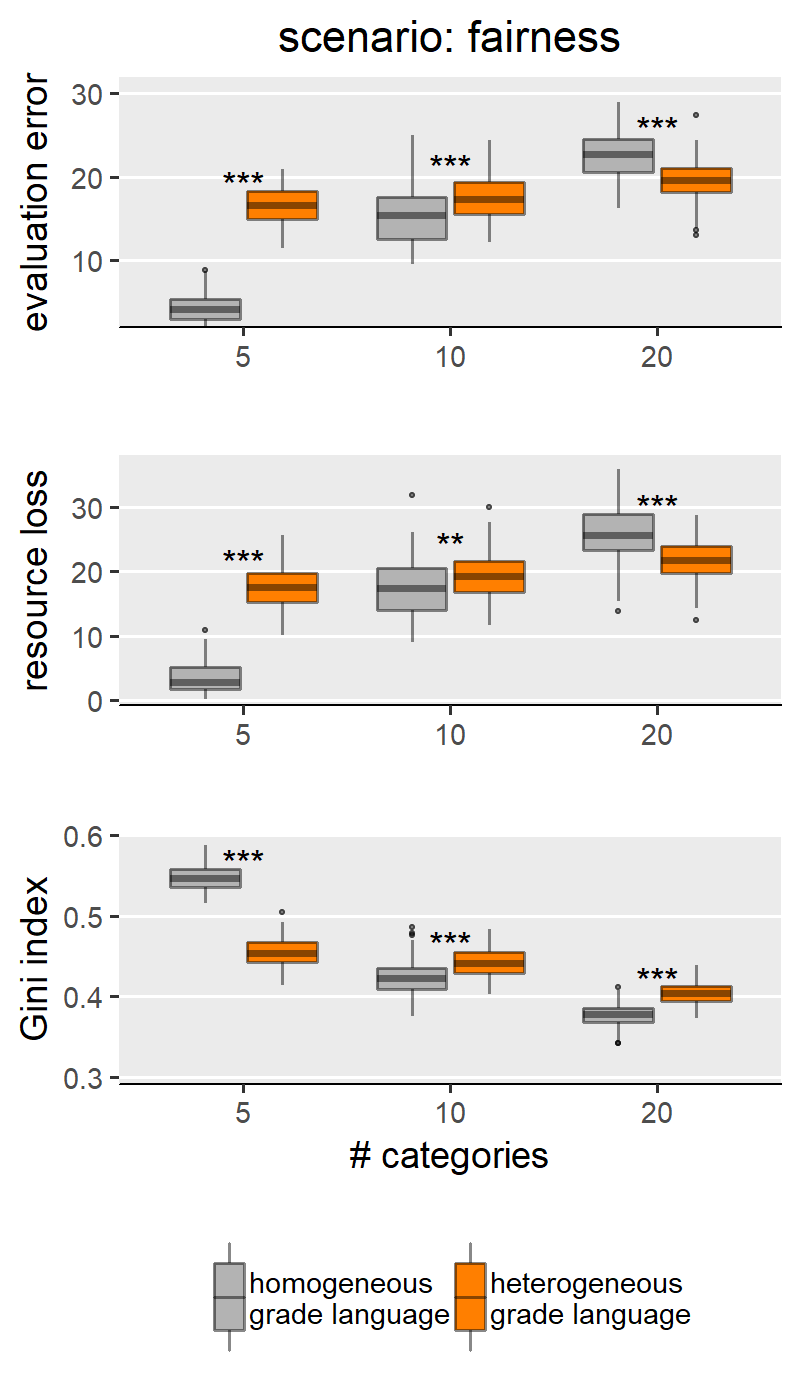
In sum, our results do not fully support H1a, b, c. We do find significant differences between homogeneous and heterogeneous grade languages under most of the simulation conditions. Yet the effect is not always in the expected direction. Some scenarios and finer-grained evaluation scales interact with grade language heterogeneity in unanticipated ways, resulting in grade language heterogeneity unexpectedly outperforming homogeneity. As discussed in Appendix II, these results are robust to another important model parameter from SG, the acceptance rate.
The result that different scenarios are affected by grade language heterogeneity in different ways bridges to H2 by means that the ordering of scenarios based on the five outcome variables varies depending on whether the grade language is homogeneous.
Effect on the relative performance of scholars’ behavioural strategies
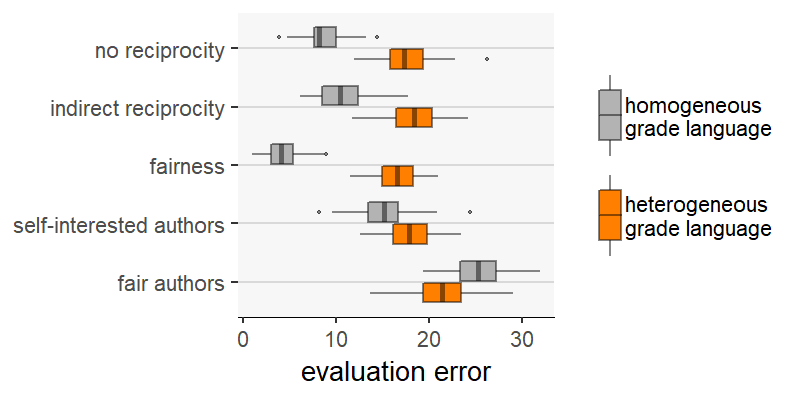
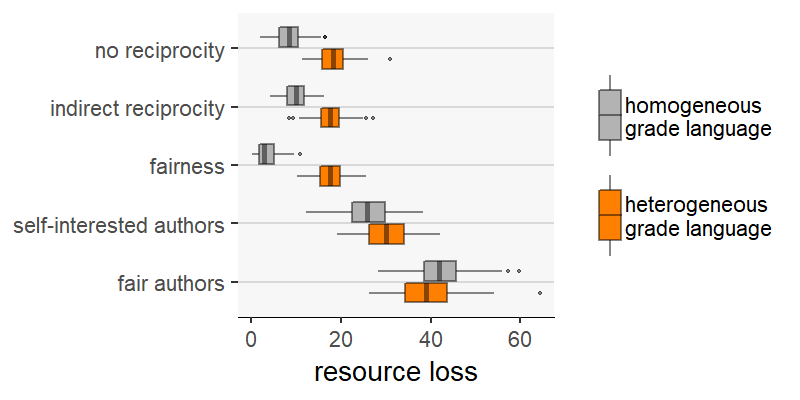
If our goal is to compare scholars’ strategies (i.e., the different scenarios), we want to ensure that whatever the predicted differences between strategies, these differences are robust to different model parameterizations (in our case, robust to the two kinds of grade languages). We have argued that grade language heterogeneity (and discrete evaluation scales) can add randomness to the measurement of some of the outcome variables (e.g., evaluation error, resource loss and Gini index), and that this effect may be different for different scenarios. Figures 5 through 9 examine the outcome one by one, allowing us to compare grade languages (homogeneous and heterogeneous) across scenarios.
Our first observation is that, compared to homogeneous grade language, heterogeneity reduces the differences between the scenarios on some outcome measures. This is true for evaluation error (Figure 5) and resource loss (Figure 6). For these two measures, markedly different scenarios are much more similar when the grade language is homogeneous. A comparison between the scenarios “indirect reciprocity” and “self-interested authors” is an extreme example. Regarding evaluation error (Figure 5), there is a strong difference between the two scenarios with homogeneous grade language, with “self-interested authors” being the scenario with the higher evaluation error. When the language is heterogeneous, however, not only does this difference disappear: “indirect reciprocity” yields, on average, slightly higher evaluation errors.
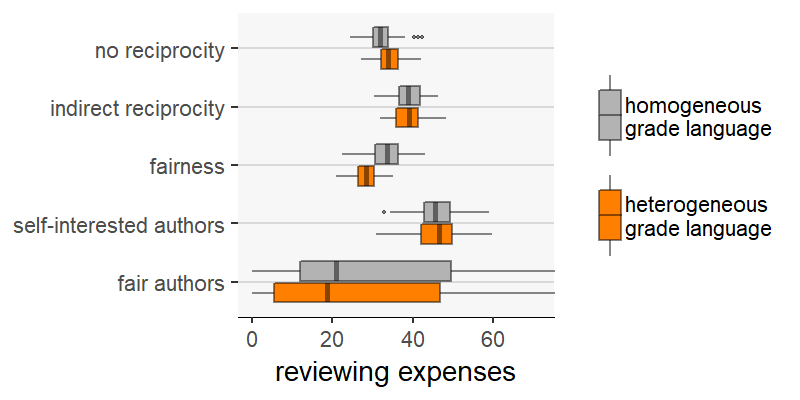
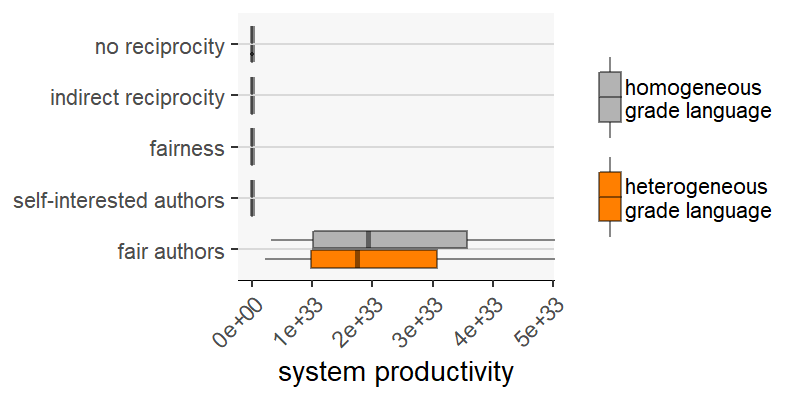
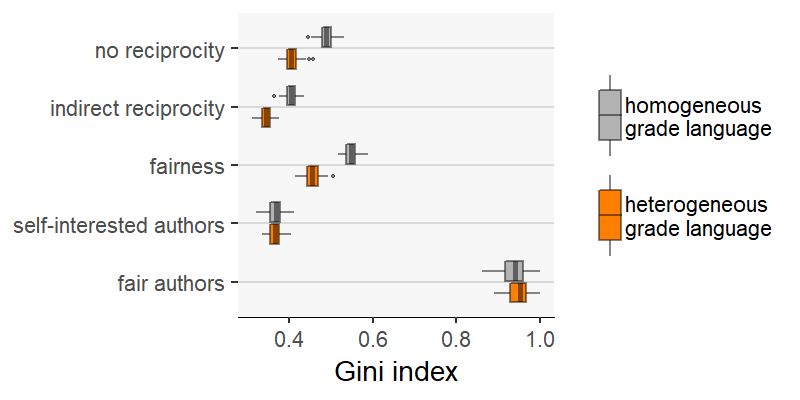
Results are somewhat different if we compare scenarios on the basis of other outcome measures: reviewing expenses (Figure 7), system productivity (Figure 8) and Gini index (Figure 9). On the one hand, with these measures we find more cases where scenarios perform better than others when assuming grade language homogeneity, but worse when the grade language is heterogeneous. The outcome variable “reviewing expenses” (Figure 7) is an example: on average, under homogeneity the scenario “no reciprocity” produces fewer reviewing expenses than “fairness”; however, it produces more with heterogeneous grade language.
On the other hand, grade language heterogeneity does not reduce the difference between the scenarios in these outcome measures (i.e., reviewing expenses, system productivity and Gini index) as it did previously with evaluation error and resource loss.
H2 is about the ordering of scenarios based on the five outcome variables varies depending on whether the grade language is homogeneous. We have found cases where heterogeneity suppresses differences between scenarios and cases where the relative performance of two scenarios reverses depending on the heterogeneity of the grade language. Thus, we conclude that H2 is supported by the results. This is an important result, as it shows that the modeller’s decision whether to assume different grading scales and grade heterogeneity can lead to very different predictions about the relative performance of the simulated scenarios. In sum, we have shown that heterogeneity in reviewers’ understanding and interpretation of an evaluation scale may have an important impact on the peer review system in terms of different aspects such as peer review efficacy, efficiency and equality. To capture this in one sentence, adding extra realism in modelling the evaluation scale does make a difference.
Conclusion and Discussion
In this paper, we have investigated the consequences of two interrelated fundamental assumptions underlying most current ABMs of peer review: (1) that the evaluation scale is continuous and (2) that reviewers understand and interpret the evaluation scale in the same way. Recent work on expert panel evaluation has shown that relaxing these assumptions can have a remarkable impact on the accuracy of the resulting evaluation (Lyon & Morreau 2018; Morreau & Lyon 2016). We follow Lyon and Morreau by assuming that (1) evaluations are expressed as grades on a discrete scale (analogous to a Likert scale); and (2) that individuals may differ between one another in how they understand the scale (called ‘grade language heterogeneity’).
To assess the impact on existing peer review ABM, we implemented discrete evaluation scales into a well-known ABM of peer review (Squazzoni & Gandelli 2012a, 2013a - or 'SG' for short). We have built on this existing model, SG, as it shares the same assumption on the grade language with most simulation models of peer review available in the literature. Many of which were derived from SG. By comparing the model dynamics with and without grade language heterogeneity, we have shown that grade language heterogeneity impacts the dynamics of the SG model in different ways for different parameter configurations. This result suggests that grade language heterogeneity should be considered as a core ingredient of future ABMs of peer review, as neglecting it would lead to unrealistic results that are ultimately inapplicable. Our approach is an explicit endeavour to avoid developing yet another simulation model that could be published and forgotten, which is a trend that has been already observed in the relevant literature of simulation models (Feliciani et al. 2019).
Scholars have advocated for the use of ABMs to observe the consequences of relaxing agent-level assumptions (Axtell 2000; Epstein 2006). Our work has shown that agent heterogeneity matters: when we relaxed a rather unrealistic assumption for modelling peer review (i.e., that all reviewers interpret evaluation scales exactly in the same way), we found that diversity in reviewers’ understanding and use of an evaluation scale can lead to important differences in the overall outcome of the peer review process.
SG is explicit in saying that the model is “highly abstracted and greatly simplified compared to in-depth empirical or experimental research” (Squazzoni & Gandelli 2013a:5.2). In this paper, we have ‘decreased the abstraction’ (Lindenberg 1992) of the SG model by adding features that more accurately reflect how peer review actually happens. Our results show that a lower level of abstraction can lead to different predictions and thus highlight contributions to better understanding peer review through agent-based modelling.
Model Documentation
Our simulation results are obtained from a re-implementation of the SG model in a different scripting language, R 3.6.1 (R Core Team 2019), whereas the original model was developed in NetLogo 4.1 (Wilensky 1999). Our re-implementation, ODD protocol (Grimm et al. 2006, 2010) and all scripts used for this paper are published in the CoMSES library as well (https://www.comses.net/codebases/35729cf6-9a2b-40ca-b895-1e4e6225f092/releases/1.0.0/). The original NetLogo code is also available on CoMSES (Squazzoni & Gandelli 2013b) and is based on the SG papers (Squazzoni & Gandelli 2013a, 2012b).Notes
- Exceptions include Righi & Takács (2017) and Paolucci & Grimaldo (2014).
- It is worth noting that, in SG, a review consists of only one grade on an evaluation scale. By contrast, in real-world peer review systems, reviews typically consist of a set of grades (because there are multiple evaluation criteria), and typically reviews are accompanied by some review text. Thus, the review grade in SG and in our own work can be interpreted as a proxy of how positive (or negative) the review is overall.
Acknowledgements
We would like to thank Michael Morreau (University of Tromsø) for the exchange of ideas which have made this work possible, and Junwen Luo (University College Dublin) for her helpful feedback on the manuscript. We also thank two anonymous reviewers for their thorough and constructive work. This material is based upon works supported by the Science Foundation Ireland under Grant No.17/SPR/5319.Appendix
Appendix A
Hereby we reference sections and quote text from Squazzoni & Gandelli (2013a) and the code of the model presented therein (Squazzoni & Gandelli 2013b). For simplicity, we refer to the paper as “SG2013a”, and to the NetLogo scripts as “SG2013b-NetLogo”.
It is important to point out that the goal of our paper is not to replicate a simulation paper from the literature. Rather, we use a simulation model from the literature to prove the point that an important theoretical ingredient is being neglected. Nevertheless, we took great care in reproducing the original model with our re-implementation. To re-implement the model we strictly followed the definitions provided in SG2013a. When necessary, we also looked into the related conference paper (Squazzoni & Gandelli 2012b) and thoroughly inspected SG2013b-NetLogo. This appendix discusses the re-implementation effort.
The process of re-implementing and testing the SG model highlighted a number of discussion points which can be d in three classes: (a) bugs or unintended artefacts in SG2013b-NetLogo; (b) incomplete model definition in SG2013a; and (c) obstacles for the replication of the results reported in SG2013a. Despite these issues, we found results reported in SG2013a to be robust (with a few caveats explained at the end of this appendix). Next, we list and discuss the issues within each of these three classes.
summarise(a) Bugs or unintended artefacts in SG2013b-NetLogo
- SG2013a:3.3 describes the fairness scenario, specifically how authors determine whether the review they have received is sufficiently accurate (i.e., “fair”). The text reads: “If the referee evaluation approximated the real value of their submission (i.e., ≥ -10%), they concluded that the referee was reliable and had done a good job”. The same statement is found in Squazzoni & Gandelli (2012b: 3), but is unclear about the exact condition for a review to be considered sufficiently accurate by the author. Upon inspection of SG2013b-NetLogo, we learned that the review is considered sufficiently accurate if the absolute difference between the submission’s true quality and the review score is strictly smaller than a tenth of the true quality. We interpreted the discrepancy between SG2013a and SG2013b-NetLogo as some text inaccuracy, and followed the implementation as in SG2013b-NetLogo.
- SG2013b-NetLogo (see e.g., “FairAuthors.nlogo”) can generate negative values for the submission quality. Negative values fall outside the defined range [0,1], and this has consequences for other parts of the code. Most prominently, the calculation of the outcome variables. This issue can be replicated by running the model with the default settings for a few iterations and then entering this command into NetLogo's console:
ask turtles [if work-quality < 0 [print work-quality]]Our re-implementation corrected this by replacing affected negative values with zero. - There is an inconsistency between text and original code concerning the calculation of reviewer’s assessment. SG2013a states that the assessment is a function of the submission’s true quality (SG2013a: 2.10). Yet the code shows that the submission quality plays no role. Instead, reviewer assessment is based on the reviewer’s estimation of the author’s resources (or ‘productivity’). That is correlated yet it is also something rather different. We attributed this inconsistency to unclear text in SG2013a, so in our re-implementation we followed exactly the procedure as implemented in SG2013b-NetLogo, where submission quality plays no role.
(b) Incomplete model definition in SG2013a
- In the “no reciprocity scenario”, reviewers behave reliably or unreliably with a given probability. SG2013a does not explain how this probability is defined: it only reads that “agents had a random probability of behaving unreliably when selected as referees; this probability was constant over time and was not influenced by past experiences” - SG2013a:3.2). Upon inspection of SG2013b-NetLogo, we find that the behaviour is drawn with a uniform probability, and reviewer behaviour is updated only if the model parameters “choose-reviewers-by-ranking” and “random-behaviour” are both set “On”. In our re-implementation we implemented this rule by setting reviewer behaviour to “reliable” with probability 0.5; “unreliable” otherwise. Following the explanation in SG2013a, we further assumed that the behaviour is updated at every time point.
- In SG2013a:2.5 the submission quality is drawn from a normal distribution with mean defined in Equation 1. The paper is not clear about how the standard deviation of this distribution is calculated. Upon inspection of SG2013a-NetLogo, we found that the standard deviation adopted is defined as follows: the product of the expected quality, times a constant (called “author investment”, or simply i), that is set by default to 0.1.
- SG2013a:2.14 mentions equation 3, the equation that should show how resources are multiplied in case of successful submission. However, equation 3 does not exist in the paper. The resources multiplier is not defined in the paper. Again, we addressed this issue by following the implementation in SG2013b-NetLogo.
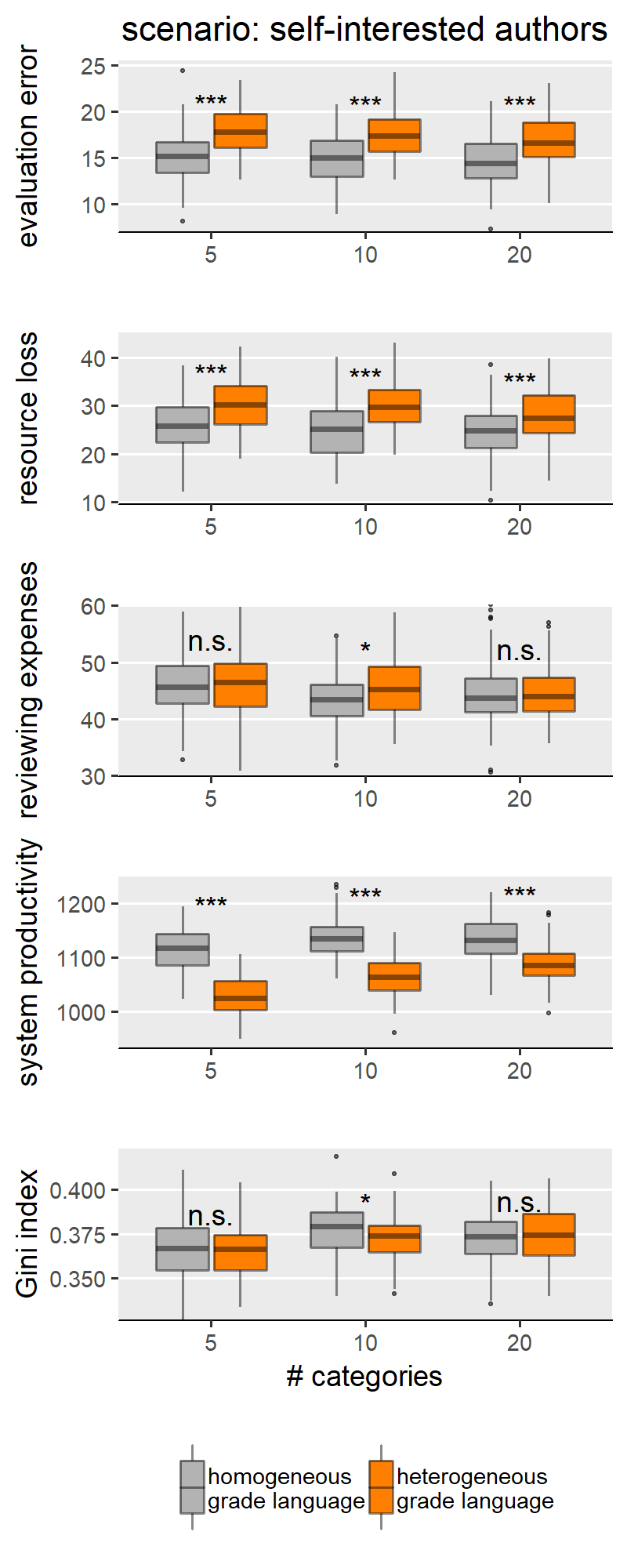
- The scenarios “self-interested authors” and “fair authors” are unique in that, unlike the other three scenarios, they manipulate authors as well as reviewer behavioural choice (SG2013a: 3.4). Reviewer and authors strategies could be considered orthogonal dimensions. For example, one could simulate a world with “self-interested authors” and “non-reciprocating reviewers”. However, in the SG model the two author scenarios are only explored in conjunction with one of the reviewers' scenarios. Specifically, the scenario “self-interested authors” is always combined with reviewers’ “indirect reciprocity”, whereas “fair authors” are always combined with reviewers’ “fairness”. This is what we extrapolated from SG2013b-NetLogo, as the text in SG2013a is not clear about the conditions for the experiments on author behaviour. The way the two author scenarios are combined with reviewer scenarios is addressed only in one short sentence, paragraph SG2013a: 3.4: “[these two scenarios] extended the previous two scenarios by examining author behaviour in conjunction with reviewer behaviour”.
(c) Obstacles to the replication of the results reported in SG2013a
The outcome variables adopted in this paper are identical to the ones used in the SG model; however, there is one crucial difference. The results in SG are based on the average across the 200 time steps of a single simulation run per condition. By contrast, our results are based on the average of these measures across the final simulation step (t=200) of 100 independent simulation runs per condition. The latter is a way of presenting results similar to the one adopted in follow-up work on the SG model (see e.g., Bianchi & Squazzoni 2015).
This way of measuring the model outcome was selected because it provides two advantages. The first advantage is the reliability of results, which are based on multiple simulation runs, so are less susceptible to random noise. The second advantage is that, by not averaging across the whole time series, we prevent highly volatile results of the first simulation steps (i.e., the so-called ‘burn-in period’) from influencing the outcome measures. The disadvantage of using this method for running simulations and presenting results is that the results from the replication are not directly comparable to those presented in SG2013a.
To minimise this disadvantage, we performed preliminary analyses where we looked at the results from our re-implementation using the same method as in SG2013a. That is, one run per condition, averaging across the time series. The results of this exercise are available in the CoMSES repository for this model, and contain a replication of the results tables and plots as in SG2013a. To summarise, we found that our re-implementation would typically replicate the results presented in SG2013a; however, we also identified some dynamics which differ from what has been originally reported.
With one exception, results reported in SG and based on single runs always fell within the range of values that we obtained from running the model 50 times. The only exception concerned the scenarios “fairness” and “fair-authors”. In these two scenarios, reviewers and/or authors decide whether or not to invest their full endowment of resources in producing accurate reviews or high-quality submissions, respectively. This decision is based on their assessment of how “fairly” their own previous submission was evaluated: if the discrepancy between the true quality of their previous submission and the received evaluation is below a given threshold, then the agents behave reliably (i.e., invest the full amount of resources in doing a good job).
In our implementation, using the same parameterization as in SG, we found that reliable behaviour fades away after a few simulation steps. This happens because as the simulation run progresses, more and more scholars deem their previous work to be evaluated unfairly and they respond by submitting poor quality papers and returning inaccurate reviews. This, in turn, translates into even more agents being evaluated unfairly, and the cycle repeats. By t=200, most agents behave unreliably. By contrast, in the original NetLogo implementation in SG, this negative feedback loop does not occur (at least not as often), and throughout the simulation run agents consistently produce more high-quality submissions and fairer reviews.
We did not investigate further the source of this difference as we deemed it irrelevant, given that the goal of this paper was not to replicate SG, but to test whether more realistic assumption on grading would make a difference. Despite this difference in the underlying dynamics between the two model implementations, the most important results on these two scenarios are qualitatively the same in SG and in the replicated condition. This difference does not affect our results. This is as, even though the difference may affect results in two points in the parameter space, our paper shows that heterogeneous grade languages lead to different results across all other SG parameter configurations.
Appendix B
This appendix reproduces the results we presented in the main text for the other parameter configurations presented in the SG model. Besides scenarios involving author and reviewer strategies, the original paper only varied the acceptance rate in the peer review process, where acceptance rate ∈ {0.25, 0.5, 0.75}. By manipulating the acceptance rate, the authors were modelling varying degrees of competitiveness between authors, where lower acceptance signifies harsher competition for publishing. In Figures 1-9 we show results for the middle value of acceptance rate (0.5). The following Figures 10-14 (i.e., one per scenario), show how acceptance rate interacts with grade language heterogeneity. These figures show that, under all three levels of competition, the assumption of grade language heterogeneity produces the same effects that we discussed in our results section. We find that homogeneous and heterogeneous grade languages differ significantly in evaluation error, resource loss and Gini index under all scenarios and all acceptance rate levels. For most scenarios, this effect is expected (i.e., as in H1a, b, c). In few cases though, the effect has the opposite sign, which we attribute to noise sources such as evaluation scale granularity or scenario-specific features.
Appendix C
This appendix reports all results integrating Figures 3 and 4. When discussing results for our H1a, b, c, we divided the five scenarios into two groups, and only showed results for one scenario representative per group. One group comprises the following scenarios: “no reciprocity”, “indirect reciprocity” and “self-interested authors”. That is, featuring effects of grade language heterogeneity generally in line with our expectations. Another group comprises of the following scenarios: “fair authors” and “fairness” – where we still found significant differences between types of grade languages, but in the opposite direction to what we expected.