Structural Effects of Agent Heterogeneity in Agent-Based Models: Lessons from the Social Spread of COVID-19

, ,
and
aGeorgia Institute of Technology, United States; bThe University of Texas at Austin, United States
Journal of Artificial
Societies and Social Simulation 25 (3) 3
<https://www.jasss.org/25/3/3.html>
DOI: 10.18564/jasss.4868
Received: 16-Dec-2021 Accepted: 08-Jun-2022 Published: 30-Jun-2022
Abstract
Modeling human behavior in the context of social systems in which we are embedded realistically requires capturing the underlying heterogeneity in human populations. However, trade-offs associated with different approaches to introducing heterogeneity could either enhance or obfuscate our understanding of outcomes and the processes by which they are generated. Thus, the question arises: how to incorporate heterogeneity when modeling human behavior as part of population-scale phenomena such that greater understanding is obtained? We use an agent-based model to compare techniques of introducing heterogeneity at initialization or generated during the model’s runtime. We show that initializations with unstructured heterogeneity can interfere with a structural understanding of emergent processes, especially when structural heterogeneity might be a key part of driving how behavioral responses dynamically shape emergence in the system. We find that incorporating empirical population heterogeneity – even in a limited sense – can substantially contribute to improved understanding of how the system under study works.Introduction
Box famously declared that all models are wrong – since then some models have been declared useful – but equally important is his caution against being “concerned about mice when there are tigers abroad” (Box 1976, p. 792). Box’s mice certainly contribute to error, but it is the tigers that contribute to erroneous understanding of the systems and phenomena under study. In the pursuit of increasingly useful models of social systems, there is value, alongside analyzing outcomes themselves, in understanding how outcomes come about. Such a structural understanding comes from bringing social science theory to bear on empirical data that captures the underlying heterogeneity of human populations. But doing so offers two openings for Box’s tigers to enter: through the operationalization of theory or through the introduction of empirical context. The central theme here is heterogeneity: individuals often display significant heterogeneity in how they act and how they respond to changing conditions. The question thus arises: how does our understanding of a system and its outcomes stem from the heterogeneity that we observe empirically as opposed to the way we model the evolution of heterogeneity over time?
In many applications, representing heterogeneity in individuals’ attributes and behaviors is critical. In epidemiological modeling, for example, connecting attributes to behaviors to outcomes can shed light on novel policy approaches for containment (Bavel et al. 2020; Gulden et al. 2021; Vermeulen et al. 2021). Agent-based models (ABMs) are particularly well suited to capturing this kind of heterogeneity. Compared to top-down, equation-based models, ABMs account for inhomogeneous mixing of populations by simulating individual-level actions and interactions and generating emergent, system-level outcomes. An ABM can incorporate agent heterogeneity in many ways (Chapuis et al. 2022). For instance, when the agents are humans, it could be through variations in age, race, income, disease susceptibility and infectiousness, interaction patterns, etc. (Crooks & Heppenstall 2012). However, increasing the level of detail in agents is only useful from a modeling perspective to the extent that the heterogeneity either informs agent behavior – e.g., interaction patterns which vary with age – or contextualizes modeling outcomes – e.g., who might become infected.
The ongoing COVID-19 pandemic has provided fertile ground for deploying ABM to understand the spread of the disease and to model interventions (Hammond 2020; Hoertel et al. 2020; Kerr et al. 2021; Lorig et al. 2021; Manzo & van de Rijt 2020; Shastry et al. 2022; Vermeulen et al. 2021). Connecting populations to sensible intervention designs requires incorporating realistic variation in the traits and behaviors of individuals, but little guidance exists on resolving uncertainty around the linkages between demographics and behavior (Amblard et al. 2015; Bavel et al. 2020; Chapuis et al. 2022). As one approaches the initialization and configuration of models of human systems, through which doors do Box’s tigers lurk? In addressing this question, we present a case study in a flexible household-level, county-scale ABM of the social spread of COVID-19. With this ABM as a testbed, we experiment with different ways of associating demographics with agent behavior. Augmenting the drivers of behavior, we discuss the effects on system level outcomes of both introducing heterogeneity during initialization and generating it over time. The following section provides background on ABMs in epidemiological modeling and contact networks. Then, we outline the empirical data on which our modeled populations are based. Next, we present the model itself, paying special attention to the ways in which we introduce and generate heterogeneity. Finally, we discuss how these changes affect the underlying mechanisms and outputs of the model.
Background
Agent-based models in epidemiology
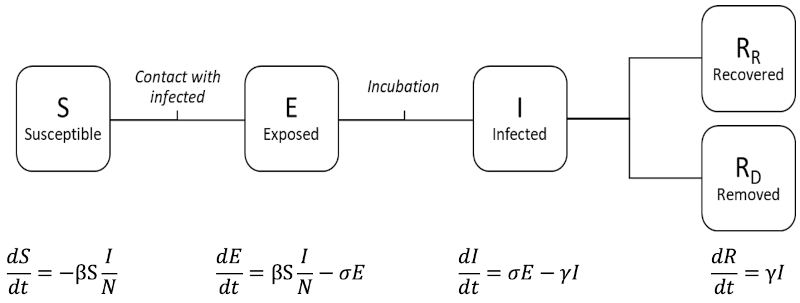
Top-down, equation-based approaches have a long history in epidemiological modeling (Kermack & McKendrick 1927). Compartmental models partition a population into compartments reflecting their disease status – e.g., Susceptible, Exposed, Infected, or Recovered (SEIR) – and model transitions from one compartment to the next as illustrated in Figure 1. At the outset of the COVID-19 pandemic, many researchers characterized the spread of the disease using SEIR models leading to estimates of progression durations and probabilities by age for the novel disease (Tec et al. 2020).
Since compartmental models place an emphasis on population-level disease dynamics, including individual behavioral responses and analyzing individual outcomes is a point of friction. Additionally, a key assumption of the compartmental model approach hinders the analysis of diverse populations. Undergirding these models is the mass-action principle – that the rate of infection spread is proportional to the product of the concentrations of susceptible and infected individuals. Implicit in this principle is the assumption of homogeneous mixing which, contrary to observed human social structures, dictates that all individuals have an equal probability of coming in contact with one another (Anderson & May 1991; Tolles & Luong 2020). This is reasonable for populations with contact patterns approximated by regular random networks (where each individual is randomly connected to the same number of other individuals), but begins to break down as the number of connections becomes increasingly variable and decreases on average (Bansal et al. 2007).
While extensions to SEIR models (Anderson & May 1979; Ball et al. 1997; Capasso & Serio 1978) can relax the mass-action assumption, ABMs avoid it entirely by incorporating individual-level resolution. In the context of COVID-19, an overall significant reduction in contact rates (Feehan & Mahmud 2021) alongside substantial variability between workers classified as essential and nonessential (Pedersen & Favero 2020) suggest the importance of inhomogeneous mixing. Heterogeneous behavioral responses to disease outbreak and subsequent public-health orders variously targeting different locales and population cohorts further motivate this modeling consideration. The use of ABMs in modeling diffusion problems in general and disease spread in particular is well established (Crooks & Hailegiorgis 2014; Dunham 2005; Koehler et al. 2021; Rai & Henry 2016). For example, Rai & Robinson (2015) used an ABM with detailed household characteristics to model how solar PV technologies diffuses through a city. Meanwhile, an early epidemiological ABM noted that compartmental models are limited by homogeneous mixing assumptions (Epstein et al. 2004). Following epidemiological literature demonstrated how the range of network structures, individual heterogeneity, and behavior that ABMs admit – as opposed to a basic, deterministic SEIR compartmental model – more faithfully reproduces the dynamics of metapopulation models while providing the modeler with more detailed and localized information (Ajelli et al. 2010; Rahmandad & Sterman 2008). Heterogeneous agents and behaviors allow ABMs to represent systems that better mimic real world conditions (Bonabeau 2002). This heterogeneity can stem from differences in agent characteristics (specified during initialization) as well as decision making rules. The resulting structure of model detail has implications for an ABM’s ability to accurately predict outcomes (Buchmann et al. 2016). This has driven interest in developing systematic approaches to incorporating empirics into ABMs (Smajgl et al. 2011; Taghikhah et al. 2021).
ABMs have been used to explore policies which limit social mobility during epidemics (Germann et al. 2006) and to show how the spread of protective or risk-seeking behaviors can be coupled with the spread of the disease itself (Epstein et al. 2008). For COVID-19, compliance with policy has been heterogeneous and played a role in mortality rates (Bargain & Aminjonov 2020). This highlights the need to modulate and extend the dynamics of simple compartmental models to capture the influence of behavioral dynamics on an epidemic’s spread (Funk et al. 2010). Such dynamics have been shown to depend both on heterogeneity in initialization and on the evolution of heterogeneous attributes (Brown & Robinson 2006; O’Sullivan et al. 2012). Separately, ABM initializations have been shown to have an impact on how agent attributes evolve (Zhang et al. 2015). In the absence of relevant empirics, it is common to initialize agents with characteristics drawn randomly from a uniform distribution (Brown & Robinson 2006; Bruch & Atwell 2015; Gilbert 2008). In both modeling contexts (epidemiological & agent-based) input data has been shown to be important.
Heterogeneity and contact networks
Departing from the homogeneous mixture assumption in an ABM requires construction of an underlying network (Amblard et al. 2015), of which the emergent contact network is a subset. Through the behaviors they help generate, these networks serve as a conduit to connect individual attributes to outcomes. When demographic data are available but empirical networks are unobserved, one approach is to seed networks by assigning agents to places (e.g., schools, offices, hospitals) and probabilistically create connections between individuals in the same location (Meyers et al. 2005). A second approach generates contact networks from empirical mobility data without a connection to individual demographic and socio-economic attributes (Frias-Martinez et al. 2011). Here, in the absence of empirical contact networks, we systematically and parsimoniously build networks based on empirical demographic data.
Several types of network constructs have been proposed and used to model different real-world systems, including (but not limited to): regular lattice, random, small world, and scale free (Amblard et al. 2015). Among the most recently conceived, small world networks (SWNs) have been shown to approximate human social networks (Wang & Chen 2003). The shape of a SWN – as a set of nodes connected by edges – lies between that of a regular lattice and random network. Randomly “rewiring” a parametrized proportion of the edges in a regular lattice to connect to different nodes yields a SWN, which approaches a random network as that proportion approaches 1. The result is densely clustered like a regular lattice with the occasional far-reaching tie to distant nodes like a random network. These two features – density and reach – are fundamentally tied to diffusion within the network (Watts & Strogatz 1998). In addition to social interactions over social networks, workplace interactions pose opportunities to spread infection. Workplace and social interactions differ in that while most individuals can curtail social contacts if needed, some employees (e.g., hospital caregivers) may not be able to reduce workplace contact rates (Meyers et al. 2005; Mutambudzi et al. 2021). Naturally, this can apply to both the employee and the recipient of employee services (e.g., hospital patient, grocery store customer). In line with this framing, we conceive of contact networks as being the outcome of three types of interactions: social interactions, and interactions in the workplace related to service provision and service receipt.
The average local clustering coefficient measures the proportion of nodes connected to a focal node that are also connected to each other – the cluster density – of an entire network. Characteristic path length – how far apart any two nodes are – measures the abundance of far-reaching ties and, in a SWN, scales with the logarithm of the number of nodes (Watts & Strogatz 1998). The degree of a node is the number of edges which connect to it; this can be decomposed for directed graphs by looking at only incoming or outgoing connections. The higher the variability of degrees across nodes, the more inhomogeneous mixing a network exhibits (Bansal et al. 2007).
In this work, we take agents with high-resolution demographic detail and estimate the SWNs that connect them based on those details. Using those networks as an input, we leverage ABM to test different ways of associating demographics with agent behavior and connections. In other words, we compare ways of introducing heterogeneity – both during initialization and over time – in the drivers of agent behavior which in turn create emergent contact networks and eventually system-level outcomes.
Data
We aim to synthesize a population of household-level agents with three key features: a rich set of characteristics, at a high spatial resolution, and with little interpolation or manipulation of input data. This is accomplished using several household-level statistics (listed in Table 1) provided by the U.S. Census Bureau’s American Community Survey 5-year (ACS5) data (U.S. Census Bureau 2018). We relate these data geospatially to census block group TIGER/Line Shapefiles (U.S. Census Bureau 2010). The result is a county-level modeled population drawn from demographic distributions specific to each block group. We then model behavioral characteristics – in the context of disease spread: risk tolerance – which are not readily available at the same scale or level of detail as the demographic variables. We also estimate weekly activity rates for essential and nonessential activities based on the American Time Use survey (U.S. Bureau of Labor Statistics 2018).
| Variable Group(s) | Description |
|---|---|
| B11001B-I | Number of households by race & ethnicity |
| B19037B-I | Age of householder by household income, race & ethnicity* |
| B11016 | Household sizes by family type |
| C24010 | Occupation breakdowns by sex |
The finest resolution data on the age of householder subdivided by income for each race/ethnicity group (B19037B-I) is at the census tract level. To overcome this and estimate the distribution for block groups, we reference another set of measures: namely, the number of households by race/ethnicity per block group (B11001B-I). In a given census tract, we calculate what proportion of households fall into each block group and use this as a weighting factor to estimate the number of households with each combination of race/ethnicity, age, and income for block groups. The ACS5 variable groups B11016 & C24010 provide further information at the block group level about household sizes and occupations, respectively. Using these three statistics, we convert the number of households in each characteristic bin to a simple probabilistic model. Importantly, the combination of B19037B-I & B11001B-I gives a joint distribution of age, income, and race. These properties are then paired with household size and occupation characteristics linked only by geography (block group). This has the effect of smoothing any inequalities in the distribution of these characteristics between income, racial/ethnic, and age groups, but captures the patterns of heterogeneity embedded in the ACS data and in the system under analysis.
In the final synthesized population, agents can have any combination of the characteristic shown in Table 2. The population size is equal to the number of households in the given county reported by ACS5. Here, we analyze Travis County, Texas which consists of 458,484 households. For computational feasibility, we select 5% random subsets of this modeled population and run 48 models in parallel. Nearly all agents of the population are included in at least one of the 48 runs. Most agents are included in multiple runs, and a few are sampled more than 10 times. The modeled population constitutes an empirical initialization: the agent characteristics are grounded in actual, recent, region-specific data.
| Age (years) | Race/ethnicity | Income $ | Size | Occupation |
|---|---|---|---|---|
| \(<\) 25 | Black or African American | Less than 10,000 | 2 | Architecture and engineering |
| 25 - 44 | American Indian and Alaska Native | 10,000 - 14,999 | 3 | Arts, design, entertainment, sports, and media |
| 45 - 64 | Asian | 15,000 - 19,999 | 4 | Building and grounds cleaning and maintenance |
| \(>\) 65 | Native Hawaiian and other Pacific Islander | 20,000 - 24,999 | 5 | Business and financial operations |
| Some other race | 25,000 - 29,999 | 6 | Community and social service | |
| Two or more races, White, not Hispanic or Latino | 30,000 - 34,999 | 7+ | Computer and mathematical | |
| White, not Hispanic or Latino | 35,000 - 39,999 | Construction and extraction | ||
| Hispanic or Latino | 40,000 - 44,999 | Educational instruction, and library | ||
| 45,000 - 49,999 | Farming, fishing, and forestry | |||
| 50,000 - 59,999 | Food preparation and serving related | |||
| 60,000 - 74,999 | Healthcare practitioners and technical | |||
| 75,000 - 99,999 | Healthcare support | |||
| 100,000 - 124,999 | Installation, maintenance, and repair | |||
| 125,000 - 149,999 | Legal | |||
| 150,000 - 199,999 | Life, physical, and social science | |||
| 200,000 or more | Management | |||
| Material moving | ||||
| Office and administrative support | ||||
| Personal care and service | ||||
| Production | ||||
| Protective service | ||||
| Sales and related | ||||
| Transportation | ||||
Methods
The voluntary nature of many public-health policies, particularly for COVID-19 in many parts of the U.S., makes policy compliance – and therefore behavioral heterogeneity – an important modeling consideration. Without enforcement, such measures are only as good as the public’s adherence to them. Essential worker designation adds another axis of behavioral differentiation to the population, since essential workers often interact with others and do not shelter in place. The reduction in contact rates implied by public-health policies and the variability between occupation designations highlights the importance of inhomogeneous mixing. Using households as the representative agents, the ABM we develop and use for the purposes of this paper captures these emergent dynamics for a population with diverse characteristics and behaviors. While the case-study presented here involves COVID-19, the modeling considerations and conclusions are relevant wherever modeled behavior stems from data. In the following subsections, we present the computational framework of the model (simulation methods), verification and validation checks, and the variations in techniques for introducing agent heterogeneity alongside the methods and metrics for comparing them (analytical methods).
Simulation methods
Agent heterogeneity manifests in two stages of the model simulation: initialization and runtime. The agent population samples described in Section 3 are the primary inputs to the ABM. Social networks are estimated among agents in a particular sample by first constraining by geographic and income homophily to reflect that agents geographically near to other agents and agents with similar socioeconomic status are likely to be connected. The social networks then become SWNs by randomly connecting agents to other agents in proportion to their original degree. Agents within the same social network do not necessarily ever come into contact – contacts are realized dynamically based on decisions driven by risk tolerance. Risk tolerance, which describes an agent’s willingness to engage in risky behavior (e.g., not wearing a mask, attending large gatherings), is initialized as a monotonically decreasing function of age. This approach is consistent both with media reports of younger people ignoring COVID-19 public-health warnings and with biological evidence that risk taking behavior decreases monotonically with age (Rutledge et al. 2016). From a policy perspective, a shelter-in-place (SIP) measure is the most interesting lever modulating the agents’ environment as it controls the designation of essential and nonessential activities and occupations.
During runtime, agents schedule three types of activities: service receipt, service provision, and social events. Scheduling depends on their risk tolerance and whether a SIP order is in effect. Essential and nonessential activities and occupations are designated based on the U.S. Center for Disease Control (CDC) and local guidelines. Service receipt represents seeking services – like medical care or food shopping – which are designated as essential during SIP. Agents receive these services regardless of policy and their risk tolerance. Service provision captures workplace activities. Before the SIP policy is active and after it is withdrawn, all agents schedule work activities where they interact with (a subset of) other agents of the same occupation category. When the SIP order is active, only workers with occupations defined by the policy as “essential” continue these interactions. While much of the modeled population reduces contacts, essential workers unintentionally end up playing a central role in disease spread as they continue interacting with the individuals receiving essential services. Social events are nonessential activities discouraged during SIP. These are considered risky activities, and agents with higher risk tolerance are likely to flout SIP and continue to engage in the social sphere. The emergent contact network is generated by these three event types: social interactions along small-world-structured networks and service provision and service receipt events across random networks. Agents can become exposed to the disease through any of the three activity types. Once exposed, agents follow a SEIR probabilistic disease progression (Tec et al. 2020), which also effects their behavior. For example, symptomatic agents curtail all three activities regardless of risk tolerance.
Agents modify their behavior – based on observations of the infection status and behavior of their peers – through two types of updates. Network updates cause agents to revise their risk tolerance based on the prevalence of the disease in their social network. This introduces both so-called “contagions of fear” (Epstein et al. 2008) and also overconfidence in the absence of caution. Event updates impact the risk tolerance of participants within a single interaction by moving the risk tolerance of all participating agents towards the group mean. This simulates the influence of social reinforcement or erosion of behaviors, for example, mask wearing. Planned interactions may or may not occur based on risk tolerance-driven decision making. For example, an agent with a large social network but a low risk tolerance, may cancel all social activities and not come into contact with anyone in their social network.
Limitations
One limitation of this model lies in the “polite” nature of the symptomatic individuals who cease all unnecessary activities. While it would be technically possible to model “impolite” symptomatic individuals, doing so would effectively eliminate the distinction between symptomatic and asymptomatic individuals (who unknowingly spread disease). Additionally, two aspects of this model design tie it closely to the U.S. policy context. First is the focus on non-compulsory policy. This contrasts with other countries where policies were legally enforceable. Second is the use of U.S. Census Bureau data. We parameterize a behavioral driver (risk tolerance) in terms of a readily observable characteristic (age). Replicating this kind of model elsewhere would require sourcing and processing empirical demographic characteristics (not necessarily age) to tie to agent behavior alongside outcome variables of interest (e.g., occupation, race/ethnicity). What observed characteristic to use in parameterizing agent behavior will depend on the application of interest and data availability.
Model verification & validation
Besides systematically debugging and checking the code for errors, we confirmed that the model produced sensible outputs when subjected to degenerate inputs (Abdou et al. 2012; Augusiak et al. 2014; Koehler et al. 2021). Specifically, we focused on ways to artificially constrain the agents’ social networks. First, we specified a small radius for local neighbors, shrinking the maximum distance at which agents can belong to the same social network before random rewiring. Second, we arbitrarily lowered the number of agents within that radius which can belong to the network. Lastly, we allowed very few nodes to be rewired, localizing networks by limiting the number of long-range social contacts. As expected, each of these constraints resulted in the disease spreading almost exclusively through essential employees. This outcome follows from the fact that if agents’ social networks are small and local, the large majority of mixing and disease spread occurs through essential interactions. By concurrently reducing the number of essential employees, the degree of bottlenecking increased even further and infectors were constrained to a very small subset of the population.
The model is calibrated to the empirical context of Travis County, Texas, USA. In this context, we establish validity at three levels: face, parameter, and process (Carley 1996). Parameter validity is established through the close ties to the empirical context (See Section 3: Data), and through the incorporation of empirical epidemiological parameters (Tec et al. 2020). Pattern validity is established as infection rates increase and subsequently slow over time, mirroring the real-world pattern of waves of spreading infection. Specifically, disease spread is initially uncontrolled before SIP is enacted (on day 28, in accordance with the empirical policy context) and dampens the spread (Figure 3) – an additional discussion of this model’s implications for SIP policy can be found in related work (Shastry et al. 2022). Furthermore, not formally but conceptually, the main results of this paper are additional forms of validation and verification with regards to risk tolerance initialization and the event and network update rules.
Analytical methods
Heterogeneous patterns in agent behavior in our model stem from agent’s risk tolerances and the social networks in which they are embedded. Each agent is initialized with some value of age-informed risk tolerance, which evolves over time. The initial assignment of risk tolerance corresponds to initial heterogeneity while the effect of model rulesets over time contribute to generated heterogeneity (Figure 2). For example, a population initialized with a low risk-tolerance (first row) will reduce contacts and tend to be less densely connected compared to a high risk-tolerance population (second row); similarly, compared to an empirical initialization (bottom row), a randomly initialized risk-tolerance (third row) will generate a less structured network. The network update and event update components of the rulesets shape the evolution of risk tolerance over time and can be toggled on or off. By mixing and matching initializations with rulesets, we experiment with different ways of introducing agent heterogeneity and observe how those initialization techniques interact with rulesets dynamically to produce emergent outcomes in the system. We present results from four distinct initializations of risk tolerance: two heterogeneous and two homogeneous. With heterogeneous starting conditions, risk tolerance is initialized as a monotonically decreasing function of age, so that older agents are less likely to engage in risky behavior. Alternatively, a random initialization is provided where risk tolerance is not a function of age and values are drawn randomly from the range of heterogeneous risk tolerances. Finally, with homogenous starting conditions, risk tolerance is initialized at the upper or lower bound of the heterogeneous risk tolerance values – simulating a uniformly risk tolerant or risk intolerant population, respectively.

Recognizing that there are many justifiable ways to initialize and update behavioral heterogeneity, we analyze the response of our model to several configurations (summarized in Table 3). For example, in model run \(A_{+N+E}\), agent risk tolerances are initialized as a function of age. Both network (\(N\)) and event (\(E\)) update rules are on, so heterogeneous individuals respond to the disease prevalence in their social networks as well as to peer pressures during interactions at social events. In contrast, model run \(L_{+N–E}\) has agents initialized homogenously with low risk tolerances. In \(L_{+N–E}\), only the network update rule is active, so these generally risk-averse agents monitor disease prevalence in their network but are not affected by peer pressure. In order to compare configurations listed in Table 3, we examine the properties of the emergent contact and exposure networks. We compare how contacts and exposures per agent vary and how closely the emergent contact network resembles the initial network. In particular, we inspect the coefficient of variation and characteristic path length in order to characterize the network type before, during, and after SIP. These intermediate outputs, as opposed to direct model outputs (e.g., in epidemiology: size and profile of the outbreak), provide more insight into how the model is working and therefore the impact of heterogeneity on model structure.
| Heterogeneous Starting Conditions | Homogeneous Starting Conditions | |||
|---|---|---|---|---|
| Network Updates | No Network Updates | Network Updates | No Network Updates | |
| Event updates | Nonuniform diffusion | Enhanced in-network diffusion | Uniform diffusion | |
| Empirical: \(A_{+N+E}\) | Empirical: \(A_{-N+E}\) | High: \(H_{+N+E}\) | ||
| Random: \(R_{+N+E}\) | Random: \(R_{-N+E}\) | Low: \(L_{+N+E}\) | ||
| No Event Updates | No normative influences | Highest sensitivity to risk tolerance formulation | Uniform diffusion without normative influences | Uniform, unmitigated diffusion |
| Empirical: \(A_{+N-E}\) | Empirical: \(A_{-N-E}\) | High: \(H_{+N-E}\) | High: \(H_{-N-E}\) | |
| Random: \(R_{+N-E}\) | Random: \(R_{-N-E}\) | Low: \(L_{+N-E}\) | Low: \(L_{-N-E}\) | |
Results & Discussion
As discussed above, in the model used for this study agent behavior is driven by risk tolerance, interaction with other agents, and response to policy context. Behavioral patterns – such as the extent of and variability in inter-agent mixing – that emerge through the model change depending on model initialization and configuration. Of specific interest is how the initializations and ruleset configurations impact not just the high-level outcomes of the model but also the mechanisms which derive those outcomes. While prior work has demonstrated that the structure of input data may not have a large impact on outcomes (Buchmann et al. 2016), the results of this study suggest that structure can indeed affect the generative mechanisms. In configurations with the same initialization, rulesets may result in only small changes in infections (e.g., Figure 3, green) despite differences in underlying contact networks (Figure 4: panel B, green). Put another way, even though two models may generate similar patterns of cumulative spread over time (Figure 3), we focus here on dissimilarities in the way the model arrives at those similar outcomes. Changes in the characteristics of the input population alter the initial heterogeneity while configurations of rulesets alter the nature of generated heterogeneity. Heterogeneity in outcomes and emergent model structure can grow from both initial and generated heterogeneity. In the ABM developed here, some degree of inhomogeneous mixing is always present, but the extent and structure of the inhomogeneous mixing – the means by which the model arrives at an outcome – is determined by a combination of initial and generated heterogeneity. Network metrics – specifically, degree and characteristic path length – and their variability and evolution over time give an indication of how the combination of initial and generated heterogeneity change the underlying dynamics of the model at a level deeper than just the outcomes (e.g., new infections).
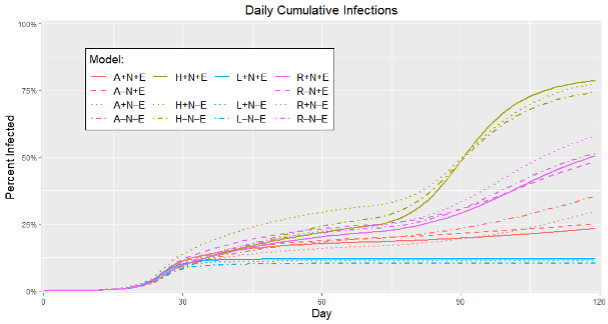
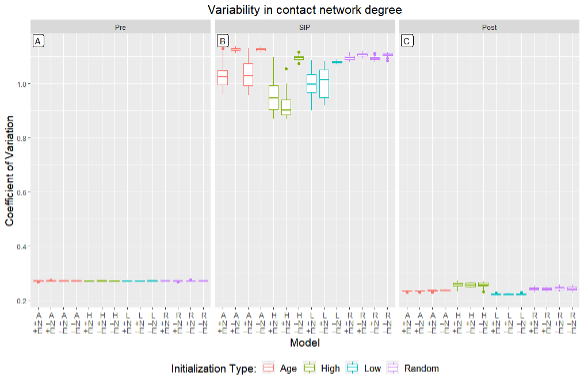
A local feature of the contact network is the number of contacts an agent makes (i.e., the degree of a node). Mixing is inhomogeneous if there is significant variability between agents. This variability in mixing – measured by the coefficient of variation (\(CV\)) – is dependent on the policies aimed at reducing contact rates. Before the start of SIP, agents are “unaware” and thus behavior interaction rules are inactive. As a result, the extent of mixing is dependent only on random encounters and the social network construction procedure, both of which are uniform between runs and models (Figure 4: panel A). During SIP, the majority of agents cease workplace activities and reduce social contacts. This drives the CV higher as essential workers experience substantially more interactions than others (panel B). In cases with non-random initial heterogeneity, enabling the network update rule (\(A_{+N+E},\) \(A_{+N-E}\), \(H_{+N+E}\), \(H_{+N-E}\), \(L_{+N+E}\), \(L_{+N-E}\)) clearly impacts the extent to which the mixing is inhomogeneous. However, with randomly initialized risk tolerances, the effect of the rule is not observed during SIP (\(R_{+N+E}\), \(R_{+N-E}\) as compared to \(R_{-N+E}\), \(R_{-N-E}\)). In these cases, the network update rule results in almost no reduction in CV – the effect is washed out by the unstructured heterogeneity in the initialization. Thus, introducing unstructured initial heterogeneity into a model where rules systematically introduce generated heterogeneity reduces the influence of those rules. After SIP, agents return to work but remain aware. The extent of inhomogeneous mixing approaches pre-SIP levels, but is moderated by lingering perceptions of risk (Figure 4: panel C).
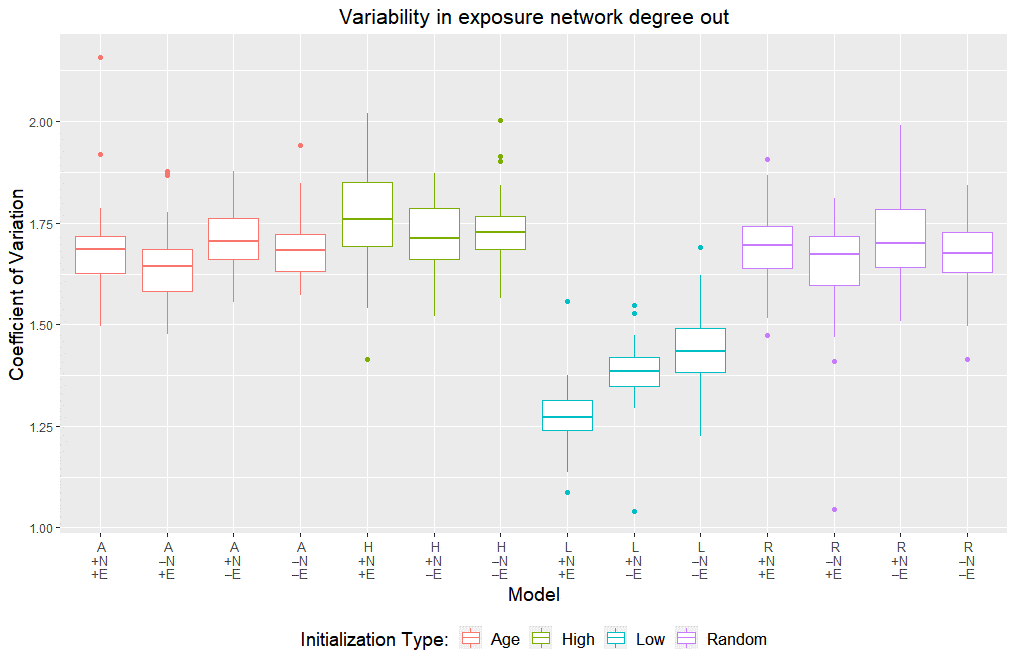
Unlike the network update rule, the event update rule does not influence whether an interaction occurs and therefore has no direct bearing on the contact network. The rule can, however, change the nature (from a risk of infection perspective) of interactions and thus the resulting exposure network – i.e., the infection degree, or number of infections caused by each agent. In general, event updates drive protective behavior (e.g., mask wearing) which limits high infection degree (superspreading) events. In the exposure networks, this is borne out as a reduction in the variability of infection degree (Figure 5: \(A_{-N+E}\) vs. \(A_{-N-E}\) & \(L_{+N+E}\) vs. \(L_{+N-E}\)). Consider the two homogeneous initializations – uniformly high risk-tolerances and uniformly low risk tolerances – as informative boundary conditions. The high risk-tolerance initialization produces the most agents willing to engage in social activities which present a threat of becoming superspreading events since they can involve many agents together. As a higher proportion of disease transmission occurs through social interactions, event updates (\(H_{+N+E}\) v. \(H_{+N-E}\)) have little moderating influence on the exposure networks: the same high risk tolerances that drive large contact networks also drive large exposure networks. In contrast, the low risk initialization produces the fewest agents willing to engage in social activities. Fewer social interactions occur to begin with and event updates (\(L_{+N+E}\) v. \(L_{+N-E}\)) curb superspreading in the remaining, mostly essential, activities where risk tolerances are not inherently high. Thus, overall, the impact of generated heterogeneity through event updates on contact and exposure network formation is relatively marginal. Next, we turn to the global impact of network updates on the contact network structure.
The characteristic path length (CPL) is another metric which can indicate how the dynamics of the model are affected by initial and generated heterogeneity. In a SWN, the average distance between nodes (or CPL) scales as the logarithm of the number of nodes. Before the start of SIP, baseline contact networks are established: a combination of each agent’s small world social network with random service provision and service receipt encounters. Panel A in Figure 6 demonstrates that this layering of small world and random networks consistently preserves the small world features – essentially, the additional random networks serve to rewire the SWN with a greater value of the rewiring parameter. As expected, the scaling of CPL/log(n) exhibits low variance between runs and models.
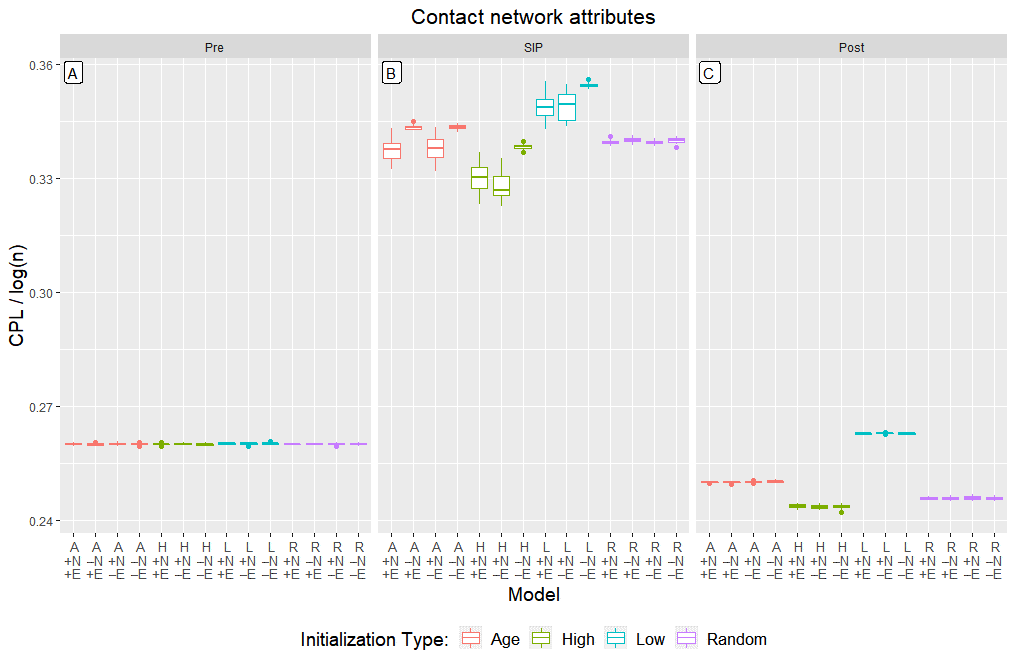
As the SIP order begins, agents revise their behavior and produce new interaction dynamics (Figure 6: panel B). In all configurations, CPL/log(n) increases as contacts are reduced and the average distance between any two agents grows. In runs with network updates and structured initialization – either empirically-sourced heterogeneity in the “A” runs or homogeneity as in the “H” and “L” runs (\(A_{+N+E}\), \(A_{+N-E}\), \(H_{+N+E}\), \(H_{+N-E}\), \(L_{+N+E}\), \(L_{+N-E}\)), the variance in this ratio also increases, suggesting that the network update rule is contributing generated heterogeneity to the structure of disease spread. When there is no accompanying increase in variance (\(A_{-N+E}\), \(A_{-N-E}\), \(H_{-N-E}\), \(L_{-N-E}\), \(R_{+N+E}\), \(R_{-N+E}\), \(R_{+N-E}\), \(R_{-N-E}\)) the structure is, in a sense, pre-determined by the original SWN formulation from before SIP. Models with unstructured initial heterogeneity do not follow this pattern: even with network update rules (\(R_{+N+E}\) & \(R_{+N-E}\)), the contact network structure is still closely related to the original SWN. Thus, when risk tolerance is initialized randomly, the subsequent structure of disease diffusion is disturbed even in the presence of behavioral elements in the model. More generally, initializing the model with unstructured heterogeneity can limit the effect of structural rules which would otherwise amplify patterns embedded in a structured initialization. After SIP (panel C), agents return to work but remain aware (e.g., H and L in panel A vs. panel C, Figure 6). Resuming workplace activities means that all agents, regardless of their risk tolerance, have many more contacts which shrinks the CPL.
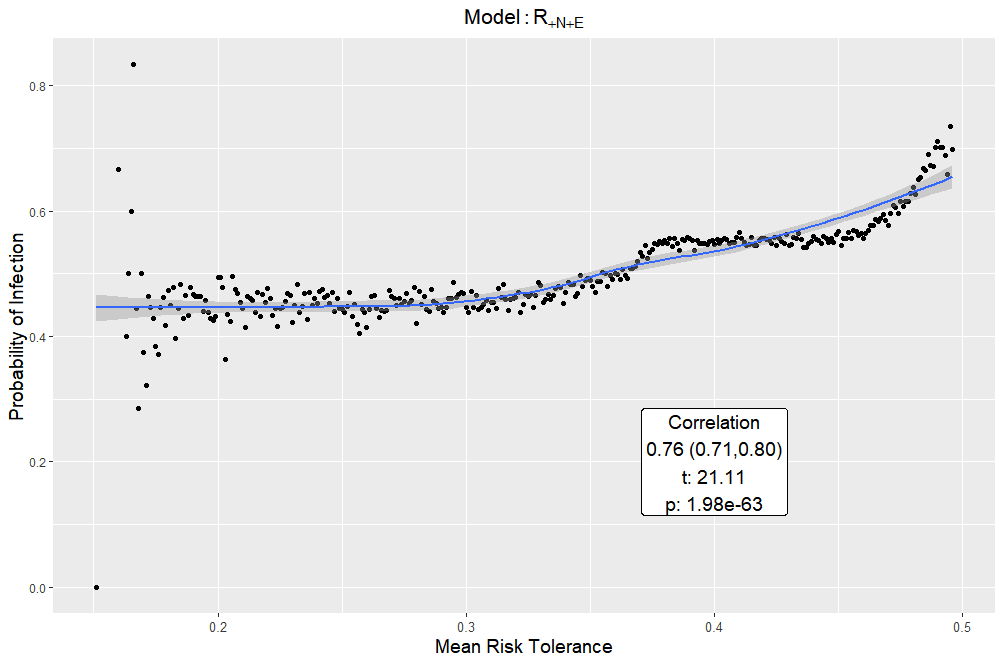
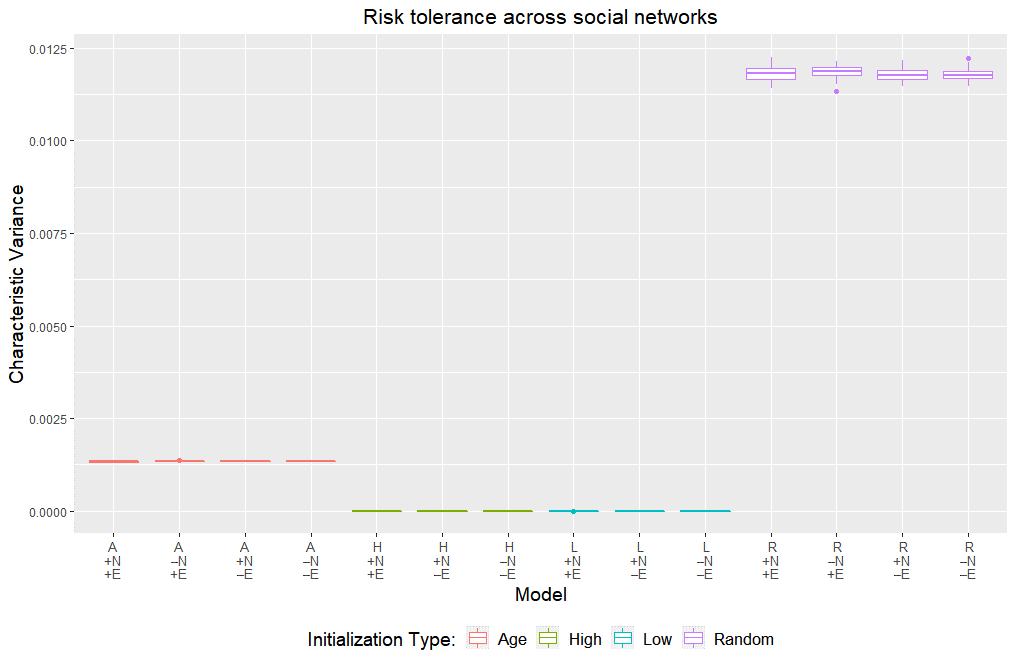
To illustrate how generated heterogeneity “picks up” initial structured heterogeneity, consider the relationship between agents’ social networks and the risk tolerances of agents therein. In models with empirical initial heterogeneity, social networks consist of agents with similar incomes; incomes and age are related since they are drawn from a joint distribution; and age is used to determine risk tolerance. Thus, risk tolerance typically varies little across socially connected agents due to the chain association of network-to-income, income-to-age, and age-to-risk tolerance. With the randomly initialized population, risk tolerance is not a function of age and the last link is broken – in fact, the variance in risk tolerance across the resulting social networks is an order of magnitude larger (see Figure 8 in the Appendix). Since risk tolerance is positively correlated with the probability of infection (see Figure 7 in the Appendix), socially localized pockets of similar infection prevalence occur under empirical initial risk tolerance. On the other hand, with randomized initial risk tolerance infection spreads without socially localized character – as risk tolerance varies more widely among socially connected agents so too does their chance of being infected. With randomized initial risk tolerance, the exposure network forms with too great a focus on the random long-distance connections of the SWN and ignores the underlying densely connected aspect of SWN structure – the result is the low variance scaling seen in Figure 6 panel B (the last four columns corresponding to ‘R’). Once again, this suggests initializing the model with unstructured heterogeneity can hamper rules which would otherwise systematically generate heterogeneity. Randomization in initialization can break structure relevant to all model configurations. Whereas the effect of randomization on the coefficient of variation (Figure 4) is a local outcome, the overall network structure that the CPL points to is global in nature. Although we assumed a functional form (based on age) for risk tolerance at the outset, these results are instead driven by the structured (A, L, or H) or unstructured (R) nature of initializations.
Conclusions
How can models of population-scale phenomena incorporate heterogeneity in a way that improves understanding and generates practical insights? To address this question, we present an agent-based model of the social spread of COVID-19 and examine the structural effects of agent heterogeneity. Our findings contribute to an understanding of how heterogeneity is best incorporated into similar agent-based models where behavior is driven by empirical agent characteristics that can change over time. In particular, we discussed ways of including different types of initial and generated heterogeneity and observed the properties of the emergent agent networks. We find that randomly initializing the model weakens the influence of agent behavioral patterns on contact and diffusion networks. Critical to the context of diffusion and, in particular disease spread, this manifests as the extent to which mixing is inhomogeneous. Understanding patterns in diffusion and disease spread at the micro-level requires realistically representing individual-level heterogeneity. We show that when model rules systematically generate heterogeneity, introducing unstructured initial heterogeneity interferes with the structural influences of those rules. We further find that this result holds not only locally in terms of the number of connections between individual agents, but is also globally in terms of the wider network structure. These results provide compelling evidence that randomly introduced heterogenous initial conditions can have the unintended effect of dampening other important features of the model, thereby preventing a reliable understanding of both micro- and macro-level phenomena. Incorporating even limited empirical evidence in initializing agent attributes that have a bearing on interactions and behaviors can provide value to a model, while random initializations can ultimately interfere structurally with the model’s relevance. Structured heterogeneity in initialization propagates through to structural patterns in emergent features even against a backdrop of random unstructured interactions. For many ABMs, uncovering actionable insight into a phenomenon depends on empirically-grounded heterogeneity in initialization or heterogeneity generated systematically through rules. When this is the case, researchers must understand the nuanced implications of introducing unstructured randomness for both emergent outcomes and the processes by which outcomes are generated.
Model Documentation
The model code and user guides are available at this link: https://github.com/RaiResearchGroup/CoPE.Acknowledgements
The authors acknowledge the helpful assistance of Hannah Rabb and Kevin Song at various stages in this project. We also appreciate the feedback on this work from participants in the UT COVID-19 Modeling Consortium, the Texas Advanced Computing Center Symposium for Texas Researchers (TACCSTER), the 2020 Computational Social Science Society of the Americas fall research conference, and the LBJ School of Public Affairs Policy, Equity, and COVID 19: From Modeling to Policymaking Webinar. All remaining errors are ours alone.Appendix
References
ABDOU, M., Hamill, L., & Gilbert, N. (2012). 'Designing and building an agent-based model.' In A. J. Heppenstall, A. T. Crooks, L. M. See, & M. Batty (Eds.), Agent-Based Models of Geographical Systems (pp. 141–165). Berlin Heidelberg: Springer.
AJELLI, M., Gonçalves, B., Balcan, D., Colizza, V., Hu, H., Ramasco, J. J., Merler, S., & Vespignani, A. (2010). Comparing large-scale computational approaches to epidemic modeling: Agent-based versus structured metapopulation models. BMC Infectious Diseases, 10(190).
AMBLARD, F., Bouadjio-Boulic, A., Sureda Gutierrez, C., & Gaudou, B. (2015). Which models are used in social simulation to generate social networks? A review of 17 years of publications in JASSS. 2015 Winter Simulation Conference (WSC), 4021–4032.
ANDERSON, R. M., & May, R. M. (1979). Population biology of infectious diseases: Part I. Nature, 280(5721), 361–367.
ANDERSON, R. M., & May, R. M. (1991). Infectious Diseases of Humans: Dynamics and Control. Oxford, MA: Oxford University Press.
AUGUSIAK, J., van den Brink, P. J., & Grimm, V. (2014). Merging validation and evaluation of ecological models to “evaludation”: A review of terminology and a practical approach. Ecological Modelling, 280, 117–128.
BALL, F., Mollison, D., & Scalia-Tomba, G. (1997). Epidemics with two levels of mixing. The Annals of Applied Probability, 7(1), 46–89.
BANSAL, S., Grenfell, B. T., & Meyers, L. A. (2007). When individual behaviour matters: Homogeneous and network models in epidemiology. Journal of the Royal Society Interface, 4(16), 879–891.
BARGAIN, O., & Aminjonov, U. (2020). Trust and compliance to public health policies in times of COVID-19. Journal of Public Economics, 192, 104316.
BAVEL, J. J. V., Baicker, K., Boggio, P. S., Capraro, V., Cichocka, A., Cikara, M., Crockett, M. J., Crum, A. J., Douglas, K. M., Druckman, J. N., Drury, J., Dube, O., Ellemers, N., Finkel, E. J., Fowler, J. H., Gelfand, M., Han, S., Haslam, S. A., Jetten, J., … Zion, R., S. R. Willer. (2020). Using social and behavioural science to support COVID-19 pandemic response. Nature Human Behaviour, 4(5), 460–471.
BONABEAU, E. (2002). Agent-based modeling: Methods and techniques for simulating human systems. Proceedings of the National Academy of Sciences, 99(3), 7280–7287.
BOX, G. E. P. (1976). Science and statistics. Journal of the American Statistical Association, 71(356), 791–799.
BROWN, D. G., & Robinson, D. T. (2006). Effects of heterogeneity in residential preferences on an agent-Based model of urban sprawl. Ecology and Society, 11(1), 46.
BRUCH, E., & Atwell, J. (2015). Agent-Based models in empirical social research. Sociological Methods & Research, 44(2), 186–221.
BUCHMANN, C. M., Grossmann, K., & Schwarz, N. (2016). How agent heterogeneity, model structure and input data determine the performance of an empirical ABM – A real-world case study on residential mobility. Environmental Modelling & Software, 75, 77–93.
CAPASSO, V., & Serio, G. (1978). A generalization of the Kermack-McKendrick deterministic epidemic model. Mathematical Biosciences, 42(1–2), 43–61.
CARLEY, K. M. (1996). Validating computational models. Available at: http://www.casos.cs.cmu.edu/publications/papers/howtoanalyze.pdf.
CHAPUIS, K., Taillandier, P., & Drogoul, A. (2022). Generation of synthetic populations in social simulations: A review of methods and practices. Journal of Artificial Societies and Social Simulation, 25(2), 6: https://www.jasss.org/25/2/6.html.
CROOKS, A. T., & Hailegiorgis, A. B. (2014). An agent-based modeling approach applied to the spread of cholera. Environmental Modelling & Software, 62, 164–177.
CROOKS, A. T., & Heppenstall, A. J. (2012). 'Introduction to agent-based modelling.' In A. J. Heppenstall, A. T. CROOKS, L. M. See, & M. Batty (Eds.), Agent-Based Models of Geographical Systems (pp. 85–105). Berlin Heidelberg: Springer.
DUNHAM, J. B. (2005). An agent-Based spatially explicit epidemiological model in MASON. Journal of Artificial Societies and Social Simulation, 9(1), 14: https://www.jasss.org/9/1/14.html.
EPSTEIN, J. M., Cummings, D. A. T., Chakravarty, S., Singha, R. M., & Burke, D. S. (2004). Toward a containment strategy for smallpox bioterror: An Individual-Based computational approach. Brookings Institution Press. Available at: https://www.brookings.edu/research/toward-a-containment-strategy-for-smallpox-bioterror-an-individual-based-computational-approach/.
EPSTEIN, J. M., Parker, J., Cummings, D., & Hammond, R. A. (2008). Coupled contagion dynamics of fear and disease: Mathematical and computational explorations. PLoS ONE, 3(12), e3955.
FEEHAN, D. M., & Mahmud, A. S. (2021). Quantifying population contact patterns in the United States during the COVID-19 pandemic. Nature Communications, 12(1), 893.
FRIAS-MARTINEZ, E., Williamson, G., & FRIAS-MARTINEZ, V. (2011). An agent-Based model of epidemic spread using human mobility and social network information. 2011 IEEE Third International Conference on Privacy, Security, Risk and Trust and 2011 IEEE Third International Conference on Social Computing.
FUNK, S., Salathé, M., & Jansen, V. A. A. (2010). Modelling the influence of human behaviour on the spread of infectious diseases: A review. Journal of the Royal Society Interface, 7(50), 1247–1256.
GERMANN, T. C., Kadau, K., Longini, I. M., & Macken, C. A. (2006). Mitigation strategies for pandemic influenza in the United States. Proceedings of the National Academy of Sciences, 103(15), 5935–5940.
GILBERT, N. (2008). Agent-Based Mmodels. Thousand Oaks, CA: SAGE Publications.
GULDEN, T. R., Hartnett, G. S., Vardavas, R., & Kravitz, D. (2021). Protecting the most vulnerable by vaccinating the most active. RAND Corporation.
HAMMOND, R. A. (2020). Developing policies for effective COVID-19 containment: The TRACE model. Brookings Institute. Available at: https://www.brookings.edu/blog/up-front/2020/05/15/developing-policies-for-effective-covid-19-containment-the-trace-model/.
HOERTEL, N., Blachier, M., Blanco, C., Olfson, M., Massetti, M., Rico, M. S., Limosin, F., & Leleu, H. (2020). A stochastic agent-based model of the SARS-CoV-2 epidemic in France. Nature Medicine, 26(9), 1417–1421.
KERMACK, W. O., & McKendrick, A. G. (1927). A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 115(772), 700–721.
KERR, C. C., Stuart, R. M., Mistry, D., Abeysuriya, R. G., Rosenfeld, K., Hart, G. R., Núñez, R. C., Cohen, J. A., Selvaraj, P., Hagedorn, B., George, L., Jastrzębski, M., Izzo, A. S., Fowler, G., Palmer, A., Delport, D., Scott, N., Kelly, S. L., Bennette, C. S., … Klein, D. J. (2021). Covasim: An agent-based model of COVID-19 dynamics and interventions. PLOS Computational Biology, 17(7), e1009149.
KOEHLER, M., Slater, D. M., Jacyna, G., & Thompson, J. R. (2021). Modeling COVID-19 for lifting non-Pharmaceutical interventions. Journal of Artificial Societies and Social Simulation, 24(2), 9: https://www.jasss.org/24/2/9.html.
LORIG, F., Johansson, E., & Davidsson, P. (2021). Agent-Based social simulation of the Covid-19 pandemic: A systematic review. Journal of Artificial Societies and Social Simulation, 24(3), 5: https://www.jasss.org/24/3/5.html.
MANZO, G., & van de Rijt, A. (2020). Halting SARS-CoV-2 by targeting high-Contact individuals. Journal of Artificial Societies and Social Simulation, 23(4), 10: https://www.jasss.org/23/4/10.html.
MEYERS, L. A., Pourbohloul, B., Newman, M. E. J., Skowronski, D. M., & Brunham, R. C. (2005). Network theory and SARS: Predicting outbreak diversity. Journal of Theoretical Biology, 232(1), 71–81.
MUTAMBUDZI, M., Niedzwiedz, C., Macdonald, E. B., Leyland, A., Mair, F., Anderson, J., Celis-Morales, C., Cleland, J., Forbes, J., Gill, J., Hastie, C., Ho, F., Jani, B., Mackay, D. F., Nicholl, B., O’Donnell, C., Sattar, N., Welsh, P., Pell, J. P., … Demou, E. (2021). Occupation and risk of severe COVID-19: Prospective cohort study of 120 075 UK Biobank participants. Occupational and Environmental Medicine, 78(5), 307–314.
O’SULLIVAN, D., Millington, J., Perry, G., & Wainwright, J. (2012). 'Agent-Based models – because they’re worth it?' In A. J. Heppenstall, A. T. Crooks, L. M. See, & M. Batty (Eds.), Agent-Based Models of Geographical Systems (pp. 109–123). Berlin Heidelberg: Springer.
PEDERSEN, M. J., & Favero, N. (2020). Social distancing during the COVID‐19 pandemic: Who are the present and future noncompliers? Public Administration Review, 80(5), 805–814.
RAHMANDAD, H., & Sterman, J. (2008). Heterogeneity and network structure in the dynamics of diffusion: Comparing agent-Based and differential equation models. Management Science, 54(5), 998–1014.
RAI, V., & Henry, A. D. (2016). Agent-based modelling of consumer energy choices. Nature Climate Change, 6(6), 556–562.
RAI, V., & Robinson, S. A. (2015). Agent-based modeling of energy technology adoption: Empirical integration of social, behavioral, economic, and environmental factors. Environmental Modelling & Software, 70, 163–177.
RUTLEDGE, R. B., Smittenaar, P., Zeidman, P., Brown, H. R., Adams, R. A., Lindenberger, U., Dayan, P., & Dolan, R. J. (2016). Risk taking for potential reward decreases across the lifespan. Current Biology, 26(12), 1634–1639.
SHASTRY, V., Reeves, D. C., Willems, N., & Rai, V. (2022). Policy and behavioral response to shock events: An agent-based model of the effectiveness and equity of policy design features. PLoS ONE, 17(1), e0262172.
SMAJGL, A., Brown, D. G., Valbuena, D., & Huigen, M. G. A. (2011). Empirical characterisation of agent behaviours in socio-ecological systems. Environmental Modelling & Software, 26(7), 837–844.
TAGHIKHAH, F., Filatova, T., & Voinov, A. (2021). Where does theory have it right? a comparison of theory-Driven and empirical agent based models. Journal of Artificial Societies and Social Simulation, 24(2), 4: https://www.jasss.org/24/2/4.html.
TEC, M., Lachmann, M., Fox, S. J., Pasco, R., Woody, S., Starling, J., Dahan, M., Gaither, K., Scott, J., & Meyers, L. A. (2020). Austin COVID-19 transmission estimates and healthcare projections.
TOLLES, J., & Luong, T. (2020). Modeling epidemics with compartmental models. JAMA, 323(24), 2515.
U.S. Bureau of Labor Statistics. (2018). American time use survey. Available at: https://www.bls.gov/tus/.
U.S. Census Bureau. (2010). TIGER/Line Shapefiles. Available at: https://www2.census.gov/geo/tiger/TIGER2010/BG/2010/.
U.S. Census Bureau. (2018). American Community Survey 5-year Estimates. Available at: https://api.census.gov/data/2018/acs/acs5.html.
VERMEULEN, B., Müller, M., & Pyka, A. (2021). Social network metric-Based interventions? Experiments with an agent-Based model of the COVID-19 pandemic in a metropolitan region. Journal of Artificial Societies and Social Simulation, 24(3), 6: https://www.jasss.org/24/3/6.html.
WANG, X. F., & Chen, G. (2003). Complex networks: Small-world, scale-free and beyond. IEEE Circuits and Systems Magazine, 3(1), 6–20.
WATTS, D. J., & Strogatz, S. H. (1998). Collective dynamics of “small-world” networks. Nature, 393(1998), 440–442.
ZHANG, J., Tong, L., Lamberson, P. J., Durazo-Arvizu, R. A., Luke, A., & Shoham, D. A. (2015). Leveraging social influence to address overweight and obesity using agent-based models: The role of adolescent social networks. Social Science & Medicine, 125, 203–213.